ТЕМА: Построение и использование регрессионной модели

ЛАБОРАТОРНАЯ РАБОТА № 3

Задание: Построить регрессионную модель с применением ЭВМ и показать ее использование (по вариантам, приведенным в исходных данных. Ниже приведен образец решения задачи.)

В таблицах для каждого варианта заданы три временных ряда:

· первый представляет нарастающую по кварталам прибыль коммерческого банка Y

· второй ряд - процентные ставки этого банка по кредитованию юридических лиц X₁

· второй ряд - процентные ставки банка по депозитным вкладам X₂ за тот же период.

Требуется:

1)Построить линейную модель регрессии, описывающую зависимость Y от факторов X₁ и X₂.

2)Оценить качество построенной модели по R и R2.

3)Проанализировать влияние факторов X1 и X2 на зависимую переменную Y.

4)Рассчитать Y при X₁=55 и X₂=45.

Вариант 1

Вариант 2

Вариант 3

Вариант 4

Y

X₁

X₂

Y

X₁

X₂

Y

X₁

X₂

Y

X₁

X₂

Вариант 5

Вариант 6

Вариант 7

Вариант 8

Y

X₁

X₂

Y

X₁

X₂

Y

X₁

X₂

Y

X₁

X₂

Вариант 9

Вариант 10

Вариант 11

Вариант 12

Y

X₁

X₂

Y

X₁

X₂

Y

X₁

X₂

Y

X₁

X₂

Вариант 13

Вариант 14

Вариант 15

Вариант 16

Y

X₁

X₂

Y

X₁

X₂

Y

X₁

X₂

Y

X₁

X₂

Регрессионный анализ позволяет получить функциональную зависимость между случайной величиной Y и некоторыми влияющими на Y величинами X. Такая зависимость получила название уравнения регрессии. Различают простую (парную) и множественную регрессию линейного и нелинейного типа.

Пример простой линейной регрессии:

y=аx+b.

Пример множественной линейной регрессии:

y=а0 +а 1x1+а2x2+... + а nxn , где n- количество факторов.

(

Для оценки степени связи между величинами используется коэффициент множественной корреляции R, который может принимать значения от 0 до 1. R=0, если между величинами нет никакой связи и R=1, если между величинами имеется функциональная (детерминированная) связь. В большинстве случаев R принимает промежуточные значения от 0 до 1. Величина R² называется коэффициентом детерминации.

Значимость R определяется не только его величиной, но и соотношением между количеством наблюдений и количеством факторов модели. Обычно для получения значимого R и достоверной регрессии необходимо, чтобы количество экспериментов существенно превышало количество коэффициентов модели .

Для проведения регрессион­ного анализа в Microsoft Excel 2007 нужно выполнить следующие действия:

· Загрузить Microsoft Excel 2007

· Подготовить и набрать на Листе Excel массив исходных статистических данных (Рис. 1)

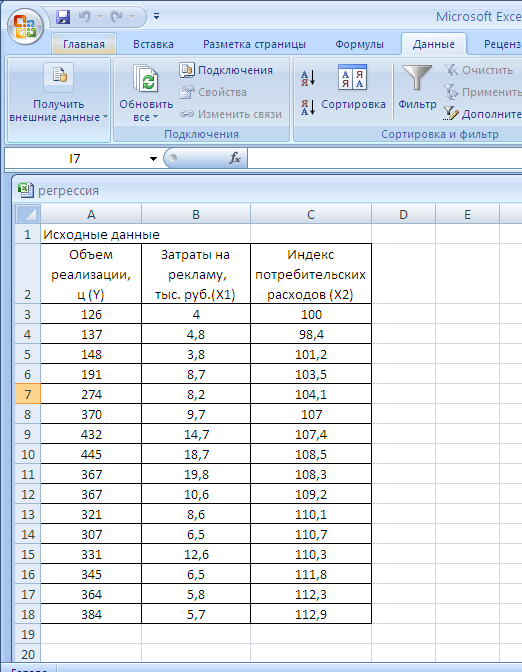
Рис.1 – Исходные данные

· В верхнем левом углу Листа щелкнуть по кнопке ▼ (настройка панели быстрого доступа) → выбрать команду «Другие команды» → «Перейти» → галочку в «Пакет анализа» → ОК →выбрать пункт меню «Данные» → в верхнем правом углу меню выбрать команду «Анализ данных» → выбрать команду «Регрессия» → ОК (Рис.2)

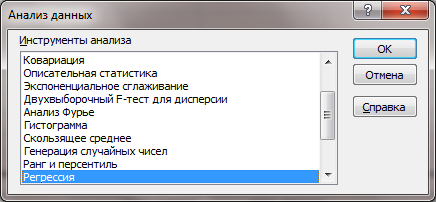
Рис.2 – Окно «Анализ данных»

· в диалоговом окне Регрессия (Рис.3) в поле “Входной интервал Y” ввести диапазон ячеек столбца Y с заголовком, в поле “Входной интервал X” ввести диапазон ячеек двух Х с заголовками

· так как выделены заголовки столбцов, то установить флажок в Метки

· ОК.

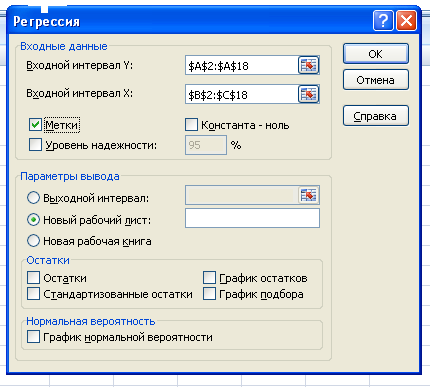
Рис.3 – Заполнение окна «Регрессия»

· В результате получаем вывод итогов в виде таблиц (Рис.4).

Результаты регрессионного анализа.

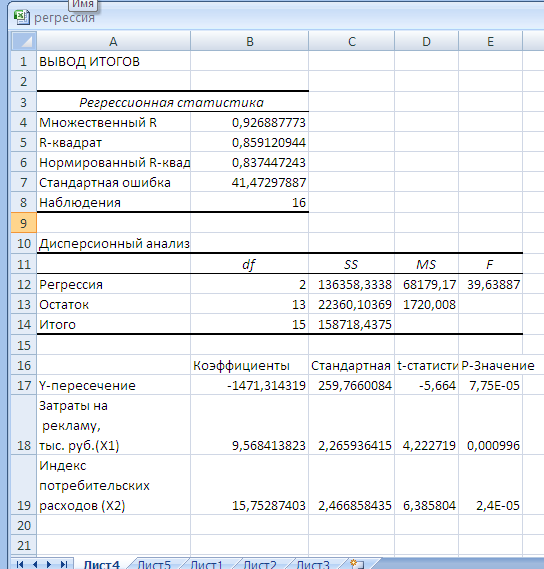
Рис.4 – Результаты регрессионного анализа

_· В последней таблице во втором столбце содержатся коэффициенты уравнения регрессии а₀, а₁, а_2.

Уравнение регрессии зависимости объема реализации от затрат на рекламу и индекса потребительских расходов имеет вид:

Y= - 1471,314 + 9,568 x₁ + 15,754 x ₂

· Для оценки качества модели используют коэффициенты корреляции R и детерминации R² , которые находятся в первой таблице результатов регрессионного анализа.

Коэффициент детерминации R² равен 0.859, он показывает долю вариации результативного признака под воздейст­вием изучаемых факторов. Следовательно, около 86% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.

· Анализ влияния факторов на зависимую переменную по модели

Коэффициент при X₁ показывает, что при увеличении расходов на рекламу на 1 тыс. руб. объем реализации вырастет на 9,568 ц.

Коэффициент при X₂ показывает, что при увеличении индекса потребительских расходов на 1 объем реализации вырастет на 15,754 ц.

· Использование уравнения регрессиизаключается в подстановке каких-либо значений факторов Х в уравнение.

Например, рассчитаем, каким ожидать объем реализации при затратах на рекламу Х₁ =15 тыс.руб. и индексе потребительских расходов Х ₂ = 110.

Подставляем Х₁ =15 и Х ₂ = 110 в уравнение регрессии:

Y= - 1471,314 + 9,568*15 + 15,754 *110 = 405,15 ц.