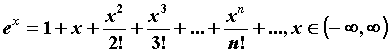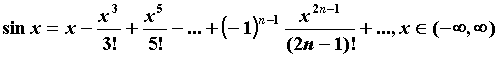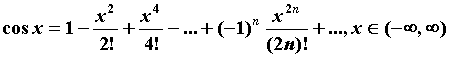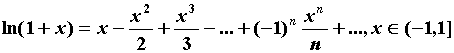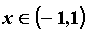Разложение функций в ряд Тейлора
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
Саратовский техникум железнодорожного транспорта - филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования
"Самарский государственный университет путей сообщения"
СТЖТ-филиал СамГупс
Реферат
На тему: «Числовые ряды. Сходимость рядов»
Дисциплина: «Математика»
Выполнил:
Студент группы Т-25в
Сунчаляев Мунир
Проверила: Лусточкина Г.Н.
Саратов 2015
Оглавление
1.Функциональные последовательности. 3
2. Функциональные ряды. 4
3 .Разложение функций в ряд Тейлора. 5
4. Разложение функции в ряд Фурье. 5
5.Разложение в ряд Фурье на произвольном отрезке. 6
6.Ряды. 6
7.Числовые ряды.. 7
1.Функциональные последовательности.
Определение. Если членами ряда будут не числа, а функции от х, то ряд называется функциональным. Исследование на сходимость функциональных рядов сложнее исследования числовых рядов. Один и тот же функциональный ряд может при одних значениях переменной х сходиться, а при других – расходиться. Поэтому вопрос сходимости функциональных рядов сводится к определению тех значений переменной х, при которых ряд сходится. Совокупность таких значений называется областью сходимости.
Так как пределом каждой функции, входящей в область сходимости ряда, является некоторое число, то пределом функциональной последовательности будет являться некоторая функция:
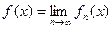
Определение. Последовательность {fn(x)} равномерно сходится к функции f(x) на отрезке [a,b], если для любого числа e>0 существует номер N = N(e), такой, что неравенство
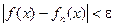 выполняется при n>N для всех точек отрезка [a,b].
выполняется при n>N для всех точек отрезка [a,b].
Пример. Рассмотрим последовательность 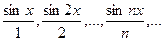
Данная последовательность сходится на всей числовой оси к функции f(x)=0, т.к.
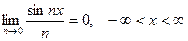 Построим графики этой последовательности:
Построим графики этой последовательности:
sinx 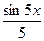
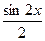
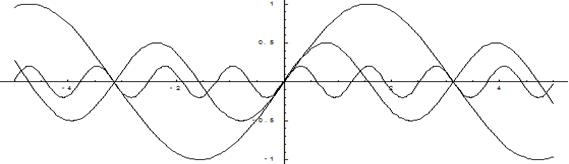
Как видно, при увеличении числа n график последовательности приближается к оси х.
Если при х = х1 ряд расходится, то он расходится для всех 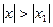 .
.
Таким образом, для каждого степенного ряда существует такое положительное число R, что при всех х таких, что 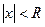 ряд абсолютно сходится, а при всех
ряд абсолютно сходится, а при всех 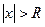 ряд расходится. При этом число R называется радиусом сходимости. Интервал (-R, R) называется интервалом сходимости.
ряд расходится. При этом число R называется радиусом сходимости. Интервал (-R, R) называется интервалом сходимости.
Отметим, что этот интервал может быть как замкнутым с одной или двух сторон, так и не замкнутым.
Радиус сходимости может быть найден по формуле:
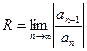 Пример. Найти область сходимости ряда
Пример. Найти область сходимости ряда 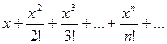
Находим радиус сходимости 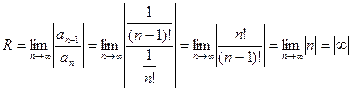 .
.
Следовательно, данный ряд сходится при любом значении х. Общий член этого ряда стремится к нулю.
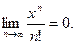
Функциональные ряды.
Определение. Частными (частичными) суммами функционального ряда 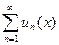 называются функции
называются функции 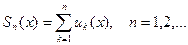
Определение. Функциональный ряд 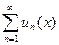 называется сходящимся в точке (х=х0), если в этой точке сходится последовательность его частных сумм. Предел последовательности
называется сходящимся в точке (х=х0), если в этой точке сходится последовательность его частных сумм. Предел последовательности 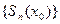 называется суммойряда
называется суммойряда 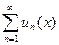 в точке х0. Определение. Совокупность всех значений х, для которых сходится ряд
в точке х0. Определение. Совокупность всех значений х, для которых сходится ряд 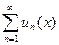 называется областью сходимостиряда.
называется областью сходимостиряда.
Определение. Ряд 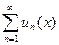 называется равномерно сходящимся на отрезке [a,b], если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.
называется равномерно сходящимся на отрезке [a,b], если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.
Разложение функций в ряд Тейлора.
При исследовании свойств бесконечно дифференцируемых функций изучают их степенные ряды Тейлора. Пусть функция 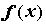 определена в некоторой окрестности точки
определена в некоторой окрестности точки 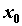 и имеет в этой точке производные всех порядков. Ряд
и имеет в этой точке производные всех порядков. Ряд
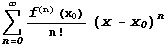 называется рядом Тейлора для функции
называется рядом Тейлора для функции 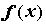 в точке
в точке 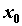 . При
. При 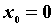 такой ряд называют также рядом Маклорена:
такой ряд называют также рядом Маклорена: 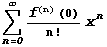 . Функция
. Функция 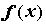 может быть разложена в степенной ряд на интервале
может быть разложена в степенной ряд на интервале 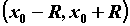 , если существует степенной ряд, сходящийся к
, если существует степенной ряд, сходящийся к 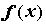 на этом интервале. Если функция раскладывается в степенной ряд в некоторой окрестности точки
на этом интервале. Если функция раскладывается в степенной ряд в некоторой окрестности точки 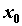 , то это ряд Тейлора. Пусть функция
, то это ряд Тейлора. Пусть функция 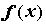 бесконечно дифференцируема на интервале
бесконечно дифференцируема на интервале 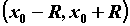 и все ее производные ограничены в совокупности на этом интервале, то есть существует число
и все ее производные ограничены в совокупности на этом интервале, то есть существует число 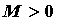 , такое, что для всех
, такое, что для всех 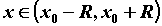 и для всех
и для всех 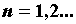 справедливо неравенство
справедливо неравенство 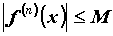 . Тогда ряд Тейлора сходится к
. Тогда ряд Тейлора сходится к 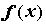 для всех
для всех 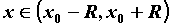 . Приведем разложения в ряд Тейлора для основных элементарных функций.
. Приведем разложения в ряд Тейлора для основных элементарных функций.