Достаточное условие экстремума
Для нахождения максимумов и минимумов функции можно пользоваться любым из трех достаточных признаков экстремума . Хотя самым распространенным и удобным является первый из них.
Первое достаточное условие экстремума .
Пусть функция y = f(x) дифференцируема в 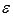 -окрестности точки
-окрестности точки 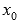 , а в самой точке
, а в самой точке 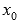 непрерывна. Тогда
непрерывна. Тогда
если 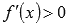 при
при 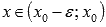 и
и 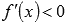 при
при 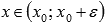 , то
, то 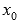 - точка максимума;
- точка максимума;
если 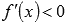 при
при 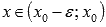 и
и 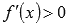 при
при 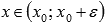 , то
, то 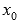 - точка минимума.
- точка минимума.
Другими словами:
если в точке 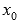 функция непрерывна и в ней производная меняет знак с плюса на минус, то
функция непрерывна и в ней производная меняет знак с плюса на минус, то 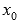 - точка максимума;
- точка максимума;
если в точке 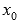 функция непрерывна и в ней производная меняет знак с минуса на плюс, то
функция непрерывна и в ней производная меняет знак с минуса на плюс, то 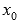 - точка минимума.
- точка минимума. 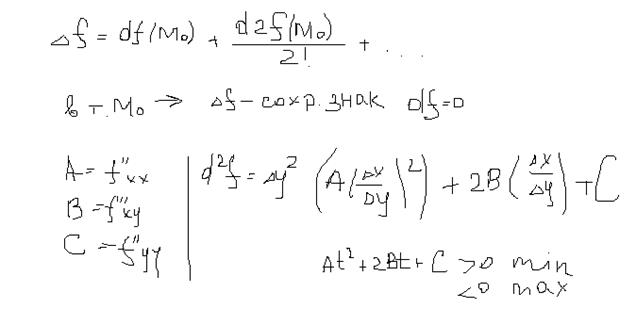
Касательная плоскости к поверхности
Пусть имеется поверхность , заданная уравнением 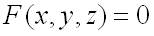 . Плоскость , в которой расположены все касательные прямые к линиям на поверхности , проходящим через данную точку
. Плоскость , в которой расположены все касательные прямые к линиям на поверхности , проходящим через данную точку 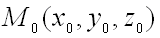 , называется касательной плоскостью к поверхности в точке
, называется касательной плоскостью к поверхности в точке 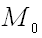 .
.
Прямая, проведенная через точку 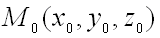 поверхности
поверхности 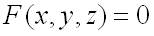 , перпендикулярно к касательной плоскости называется нормалью к поверхности .
, перпендикулярно к касательной плоскости называется нормалью к поверхности .
Если поверхность задана уравнением 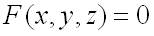 , то уравнение касательной плоскости к этой поверхности в точке
, то уравнение касательной плоскости к этой поверхности в точке 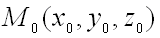 записывается в виде:
записывается в виде:
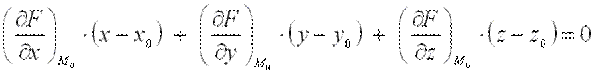 ,
,
а уравнение нормали к поверхности в этой же точке – в виде:
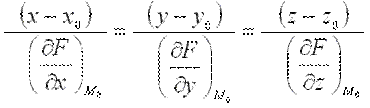 .Примеры решения задач
.Примеры решения задач
Пример 1. Найти уравнение касательной плоскости и нормали к поверхности 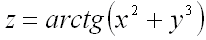 в точке
в точке 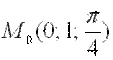 .
.
Решение.
Уравнение касательной плоскости к поверхности , заданной уравнением 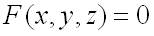 , в точке
, в точке 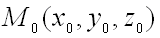 записывается в виде:
записывается в виде: 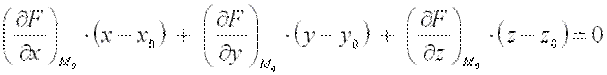 .
.
Так как в условии задачи уравнение поверхности задано в явном виде, то сначала его необходимо преобразовать к виду 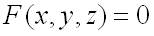 :
: 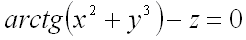 .
.
Теперь найдем частные производные 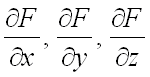 (при этом, в первых двух случаях используем правило дифференцирования сложной функции одной переменной):
(при этом, в первых двух случаях используем правило дифференцирования сложной функции одной переменной):
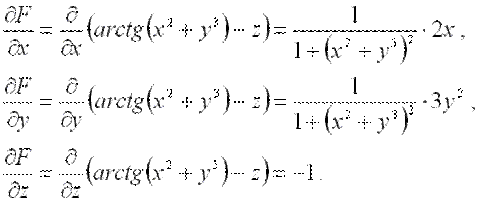
Вычислим значения частных производных первого порядка в точке 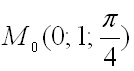 :
:

Подставим полученные значения в уравнение касательной плоскости :
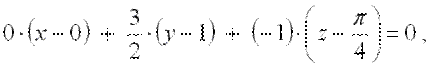
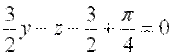 .
.
Нормальная прямая к поверхности
Прямая , проходящая через точку касания перпендикулярно касательной плоскости к поверхности , называется нормалью к этой поверхности , проведённой в точке , или нормальной прямой .
Вектор-градиент
Градиент ), вектор , показывающий направление наискорейшего изменения некоторой величины, значение которой меняется от одной точки пространства к другой. Если величина выражается функцией u (х, у, z), то составляющие Г. равны 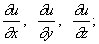 Г. обозначается знаком grad u. Г. в некоторой точке направлен по нормали к поверхности уровня в этой точке, длина Г. равна
Г. обозначается знаком grad u. Г. в некоторой точке направлен по нормали к поверхности уровня в этой точке, длина Г. равна
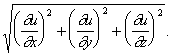
Понятием Г. широко пользуются в физике, метеорологии, океанологии и др., чтобы охарактеризовать скорость изменения в пространстве какой-либо величины при перемещении на единицу длины в направлении Г.: например, Г. давления, Г. температуры, Г. влажности, Г. скорости ветра, Г. солёности, Г. плотности морской воды. Г. электрического потенциала называется напряжённостью электрического поля.
