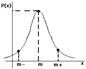
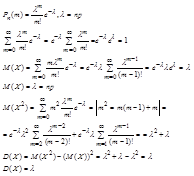Интегральная теорема Муавра-Лапласа

Перестановки.

Перестановками наз. комбинации из n элементов, отличающихся друг от друга лишь местоположением элементов.

n=2 - ab,ba; n=3 – abc, acb, bac, bca, cba, cab.

P_n=n!

Сочетания.

Сочетания из n элементов по m элементов наз. комбинации, отличающихся друг от друга лишь составом элементов.

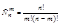
Пример: Из 12 разведчиков в разведку надо отправить 3.

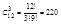
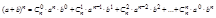Размещения.

Размещениями наз. комбинации из n элементов по m элементов, отличающиеся друг от друга не только составом элементов, но и их месторасположением.

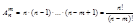
Пример. На разведку минного поля из 12 разведчиков надо послать 3.

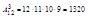
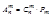
2. Условная вероятность. Независимое событие. Формула умножения вероятности.

Условная вероятность.

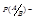условная вероятность(вероятность события А при условии, что произошло событие В).

;

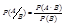Пусть произведению событий А и В благоприятствуют m исходов, событию В – k исходов. Общее число возможных и равновозможных исходов = n.

; ;

.

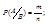
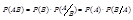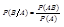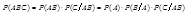Независимые события.

Событие А и В наз. независимыми, если P(AB)=P(A)P(B);

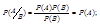
События наз. попарно независимыми, если для любой пары P(A_i,A_j)=P(A_i)P(A_j), .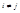

События наз. A₁,A₂…A_n независимыми в совокупности, если P(A₁,A_2….A_n)=P(A₁)P(A₂)..P(A_n);

Вероятность наступления хотя бы одного события.

Пусть события А_1,А_2..А_n независимы в совокупности, тогда

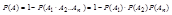ж

Если вероятность события обозначить 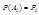, то вер-ть противоположного события обозн. .

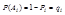P(A)=1-q₁q₂..q_n.

Когда А_1…А_n равновероятны, то .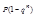

3. Ф-ла полной вероятности. Формула Байеса.

Пусть события Н₁, Н₂, … ,Н_n, во-первых, попарно не совместны. 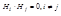, и во-вторых, они образуют полную группу событий.

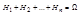, тогда Н₁, Н₂, … ,Н_n наз. гипотезами. Пусть некоторое событие А может наступить одновременно с какой-то из гипотез Н₁, Н₂, … ,Н_n. Поэтому А=АН₁+АН₂+…+АН_n. P(A)=P(H₁A+H₂A+…+H_nA)=P(H₁A)+ P(H₂A)+…+ P(H_nA)=

P(H₁)P(A/H₁)+ P(H₂)P(A/H₂)+… P(H_n)P(A/H_n).

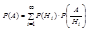. (1)

Формула Байеса.

Событие А свершилось. В ф-ле (1) считается вероятность до опыта (априорная), в ф-ле Байеса происходит пересчет гипотезы после опыта (апосториорная).

.

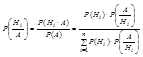4.Последовательность независимых испытаний. Схема Бернулли. Формула Пуассона.

Пусть проводится серия из n одинаковых испытаний, в каждом из кот. событие А может произойти с одной и той же вероятностью р (в-ть успеха) и не произойти с одной и той же вероятностью q (в-ть неудачи) q=1-p. Наступление либо не наступление события А в n-ом испытании не зависит от исхода предыдущих испытаний.

P_n(m) из n испытаний событие произойдет ровно n раз.

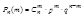— формула Бернулли.

P_n(0)+P_n(1)+ P_n(2)+…+ P_n(m)+…+ P_n(n)=(q+p)ⁿ=1.

При помощи этой формулы событие произойдет больше m раз: P_n(m+1)+ P_n(m+2)+…+ P_n(n).

Формула Бернулли применяется, когда n — невелико (не больше 10). Если n>10, то на практике применяют: локально-интегральную теорему Муавра-Лапласа, а также формулу Пуассона.

Формула Пуассона

n- велико, порядка сотен и тысяч.

p- мало, порядка сотых и тысячных.

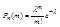, где ; .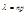

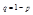5.Наивероятнейшее число наступления события.

Вероятность можно рассматривать как функцию целочисленного аргумента m.

Существует такое значение аргумента 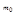, при котором эта функция принимает наибольшее значение

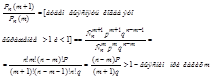np-mp>mq+q

m(q+p)<np-q, где q+p=1

m<np-q

Вывод при таких m 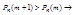при таких m функция возростает.

И наоборот при

m>np-q

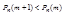, то есть при таких m функция убывает, то есть действителен один 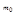при котором функция достигает max значения

По смыслу 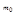должны выполняться два неравенства

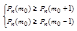
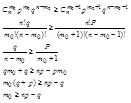
Распишем 2-е неравенство

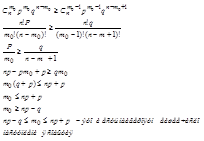
6. Локальная теорема и интегральная теорема Муавра-Лапласа.

Локальная теорема.

Применяется, когда 0<P<1 или не слишком близко к 0 или 1.

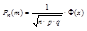
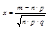
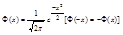
Интегральная теорема Муавра-Лапласа.

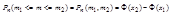
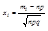, i=1,2,3,…

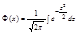- функция Лапласа (интеграл ошибок, интеграл вероятностей)

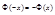
Пример 300 дет. за смену

Р(1-ого сорта)=0.75 q=0.25

а) 225 штук б) от 210 до 240

а)

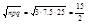
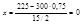
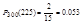
б) ; ;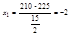

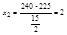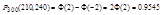
7. СВ. Функции распределения и их свойства.

СВ наз. величины к-рые могут принимать те или иные значения заранее до опыта неизвестно какие именно. Различают дискретные и непрерывные СВ.

Дискретные СВ.

Значения обознач х₁,х₂,…,х_n,…

Всякое описание значений, к-рые может принимать СВ и соответствующие этим значениям вероятности наз. законом распределения СВ.

Для дискретной СВ:

xi	X1	X2	…	xn
pi	P1	P2	…	pn

;

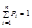Пример:

Вер. Того что в библиотеке нужная ему книга свободна равна 0,3. В городе 4 библиотеки. СВХ – это число библиотек к-рое посетит студент. Составить з-н распределения СВ.

xi
Pi	0.3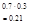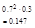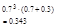

Ф-ция распределения СВ.

Ф-цией распределения или интегральной ф-цией наз. F(X)=P(X<x). Вер.того вер.Х меньше чем х:

xi	X1	X2	…	xn
pi	P1	P2	…	pn

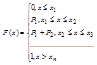
Свойства:

1.

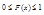
2.F(X)-функция неубывающая

X₁ X₂ X

Рассмотрим событие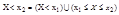

;

;

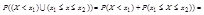
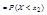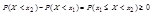
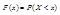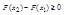
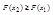-большему значению аргумента соответствует большее значение функции.

3.

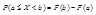
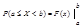
Замечание: если случ. Величина X непрерывна то вероятность того что СВХ примет значение х равна 0.

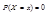ж

8.Числовые хар-ки случайной величины.

Математическое ожидание:

На практике часто полное описание случайной величины не слишком важно, достаточно знать нек. параметры. Их называют числовыми характеристиками. Наиболее важная – мат. ожидание или её среднее значение (М(Х))

xi	X1 – Xn
pi	P1 - Pn

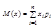
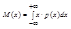
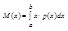
Дисперсия случайной величины:

Дисперсия характ. Разброс значений СВ около своего среднего значения (показатель рассеивания)

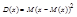
Дисперсия – мат. ожидание от квадрата отклонения СВ от своего мат. ожидания

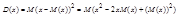
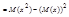;где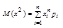

Среднее квадратичное отклонение: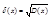

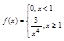
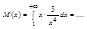
Пример: 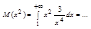и т.д.

9.Биномиальный закон распределения.

Говорят, что СВ распределена по биномиальному закону, если она принимает значения 0, 1, 2, …, m, …,n а соответствующие вероятности вычисляются по формуле Бернулли:

0 - P_n(0), 1 – P_n(1), m – P_n(m), n – P_n(n)

; ; ; ; ;

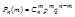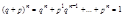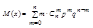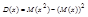
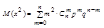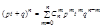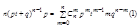
В (1) положим t=1

; ; ; ;

;

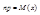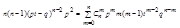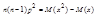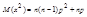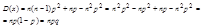
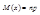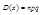
10.Распределение Пуассона. Равномерное распределение.

СВ распределена по закону Пуассона, если она принимает значения 0, 1, 2, 3,…, m,…,n, а соответсвующие вероятности по формуле Бернулли.