Способы интегрирования некоторых других классов функций
Интегралы вида
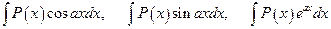 , (4.1)
, (4.1)
где 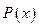 - многочлен, берутся по частям, причем за u берется
- многочлен, берутся по частям, причем за u берется 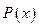 . Интегрировать по частям нужно столько раз, какова степень многочлена
. Интегрировать по частям нужно столько раз, какова степень многочлена 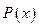 .
.
Пример. 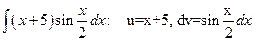
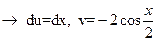 ;
;
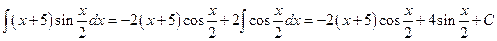 .
.
Интеграл вида
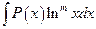 , (4.2)
, (4.2)
где 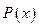 - многочлен, берется по частям. При этом за
- многочлен, берется по частям. При этом за 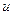 берется
берется 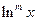 .
.
Пример. 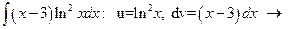
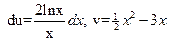 ;
;
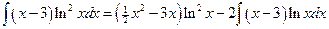 .
.
Вычисляем 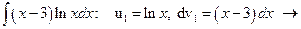
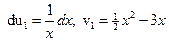 ;
;
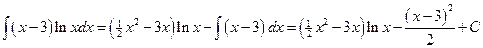 .
.
Следовательно,
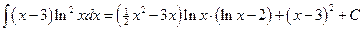 .
.
Пусть 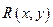 - рациональная функция переменных х и у. Интегралы вида
- рациональная функция переменных х и у. Интегралы вида
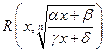 (4.3)
(4.3)
сводятся к интегралам от рациональных функций подстановкой
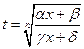 . (4.4)
. (4.4)
Действительно, из (4.4) находим:
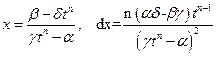 . 4.5)
. 4.5)
Пример. 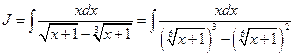 .
.
Обозначим 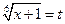
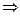
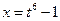 ,
, 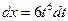 . Следовательно,
. Следовательно,
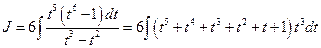 =
=
= 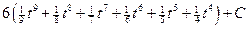 =
=
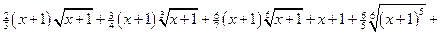
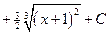 .
.
Выражение
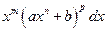 , (4.6)
, (4.6)
где 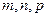 - рациональные числа, называется биномиальным дифференциалом. Их интегрирование сводится к интегрированию дробно-рациональных функций только в трех случаях:
- рациональные числа, называется биномиальным дифференциалом. Их интегрирование сводится к интегрированию дробно-рациональных функций только в трех случаях:
1) 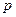 - целое, подстановка
- целое, подстановка 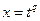 , где
, где 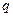 - общий знаменатель дробей m и n;
- общий знаменатель дробей m и n;
2) 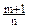 - целое, подстановка
- целое, подстановка 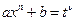 , где
, где 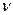 - знаменатель числа р;
- знаменатель числа р;
3) 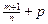 - целое, подстановка
- целое, подстановка 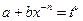 .
.
Выдающийся русский математик П.Л. Чебышёв доказал, что только в этих трех случаях интегралы от биномиальных дифференциалов (4.6) выражаются через элементарные функции.
Примеры. №1. 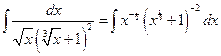 .Здесь
.Здесь 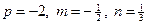 , т.е. имеем 1ый случай (р - целое). Положим:
, т.е. имеем 1ый случай (р - целое). Положим: 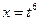
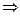
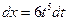 ,
,
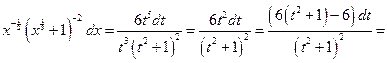
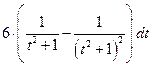 .
.
Следовательно,
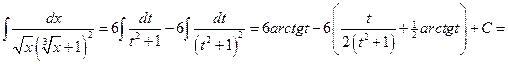
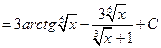 .
.
№2. 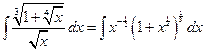 .
.
Здесь 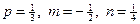 , т.е.
, т.е. 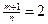 - целое. Имеем 2ой случай. Полагаем
- целое. Имеем 2ой случай. Полагаем 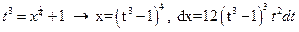 . Следовательно,
. Следовательно,
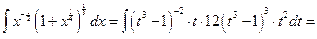
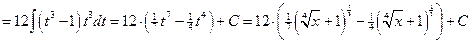
№3. 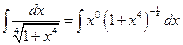 .
.
Здесь 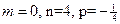 . Имеем 3й случай. Положим
. Имеем 3й случай. Положим 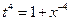
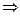
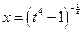 ,
, 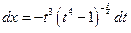 ,
, 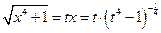 . Следовательно,
. Следовательно,
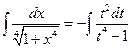 .
.
Имеем:
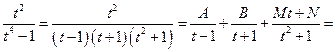
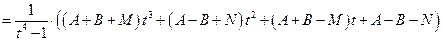 ,
,
т.е.
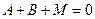 ,
, 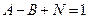 ,
, 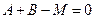 ,
, 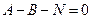 ®
®
® 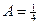 ,
, 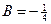 ,
, 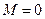 ,
, 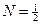 .
.
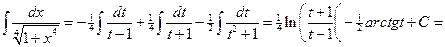
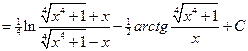 .
.
Интегралы вида
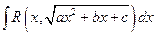 ,
, 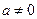 (4.7)
(4.7)
сводятся к интегралам от дробно-рациональных функций одной из трех подстановок Эйлера:
1) 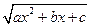 =
= 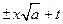 , если
, если 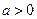 ; (4.8)
; (4.8)
2) 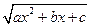 =
= 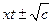 , если
, если 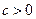 ; (4.9)
; (4.9)
3) 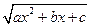 =
= 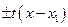 или
или 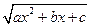 =
= 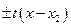 , (4.10)
, (4.10)
если 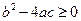 , а
, а 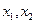 - корни квадратного трехчлена.
- корни квадратного трехчлена.
Примеры. №1. 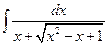 .(
.( 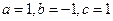 , 1ая или 2ая подстановки). Положим
, 1ая или 2ая подстановки). Положим 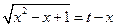 ®
®  ,
, 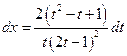 ,
, 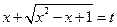 . Имеем
. Имеем
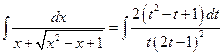 ;
;
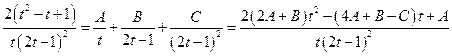 .
.
Следовательно, 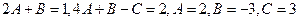 .
.
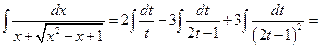
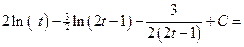
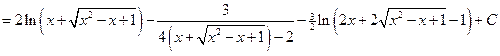 .
.
№2. 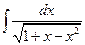 .(
.( 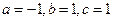 , 2я или 3я подстановки). Положим
, 2я или 3я подстановки). Положим 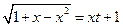 ®
® 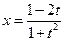 ,
, 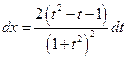 ,
, 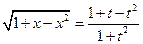 . Следовательно,
. Следовательно,
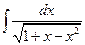 =
= 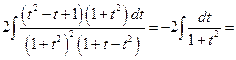
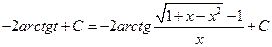 .
.
№3. 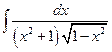 .(
.( 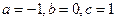 , 2я или 3я подстановки). Положим
, 2я или 3я подстановки). Положим 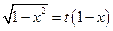
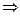
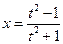 ,
, 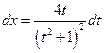 ,
, 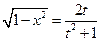 ,
, 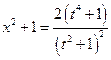 ,
, 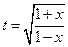 . Следовательно,
. Следовательно,
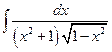 =
= 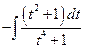 .
.
Имеем:
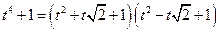 ;
;
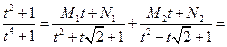
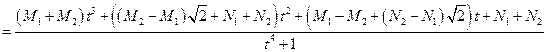
т.е. 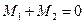 ,
, 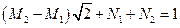 ,
, 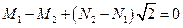 ,
, 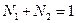 .
.
Следовательно, 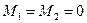 ,
, 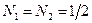 . Значит,
. Значит,
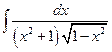 =
= 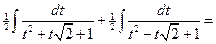
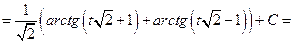
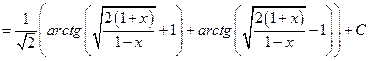 .
.
Интегралы вида
 , (4.11)
, (4.11)
где 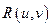 - рациональная функция двух переменных, сводятся к интегрированию дробно-рациональных функций универсальной подстановкой
- рациональная функция двух переменных, сводятся к интегрированию дробно-рациональных функций универсальной подстановкой
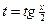 . (4.12)
. (4.12)
Действительно,
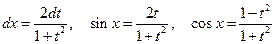 . (4.13)
. (4.13)
Пример. 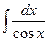 . Положим:
. Положим: 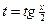
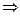
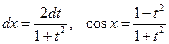 . Имеем:
. Имеем:
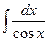 =
= 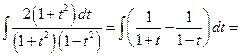
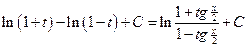 .
.
7.Интегралы вида
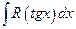 , (4.14)
, (4.14)
где 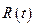 - рациональная функция, удобнее брать с помощью подстановки:
- рациональная функция, удобнее брать с помощью подстановки:
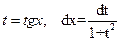 . (4.15)
. (4.15)
Пример. 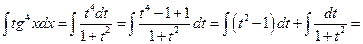
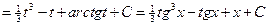 .
.
Интегралы вида
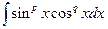 , (4.16)
, (4.16)
где 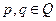 , т.е. рациональные числа, подстановкой
, т.е. рациональные числа, подстановкой
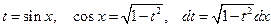 (4.17)
(4.17)
приводятся к интегралам от биномиальных дифференциалов. Действительно,
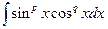 =
= 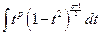 .
.
На основании критерия Чебышева этот интеграл выражается через элементарные функции лишь в трех случаях, когда одно из чисел:
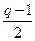 ,
, 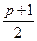 ,
, 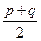 (4.18)
(4.18)
является целым числом. В частности, если оба числа 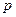 и
и 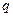 - целые, то это условие выполняется, т.к. если одно (или два) из этих чисел - нечетные, то целым будет
- целые, то это условие выполняется, т.к. если одно (или два) из этих чисел - нечетные, то целым будет 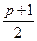 или
или 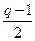 , или все три. Если же p и q - четные числа, то число
, или все три. Если же p и q - четные числа, то число 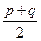 - целое.
- целое.
Интегралы вида
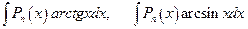 , (4.19)
, (4.19)
где 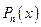 - многочлен степени
- многочлен степени 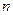 , берутся по частям. Полагают:
, берутся по частям. Полагают:
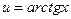 ,
, 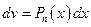 , (4.20)
, (4.20)
или
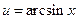 ,
, 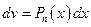 . (4.21)
. (4.21)
Пример. 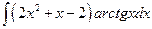 .
.
Положим: 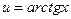 ,
, 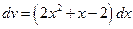 ®
® 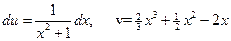 .
.
Следовательно,
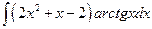 =
= 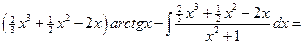
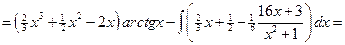
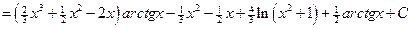 .
.
Аналогичным способом берутся интегралы вида
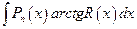 , (4.22)
, (4.22)
где 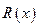 - рациональная функция.
- рациональная функция.
В заключение заметим, что рассмотренные способы интегрирования далеко не исчерпывают все многообразие приемов интегрирования. Из изложенного следует, насколько операция интегрирования сложнее операции дифференцирования. Если продифференцировать можно любую элементарную функцию, то обратная операция - интегрирование даже в принципе иногда не разрешима в элементарных функциях. Такие интегралы называются интегралами не выражающимися в квадратурах. К их числу, например, относятся интегралы:
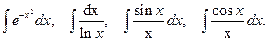 (4.23)
(4.23)
