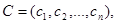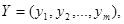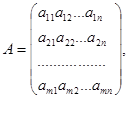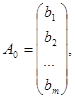Теория двойственности
Виды математических моделей двойственных задач.
Любой задаче линейного программирования (исходной, или прямой) можно поставить в соответствие другую задачу, которая называется двойственной, или сопряженной. Обе эти задачи образуют пару двойственных (или сопряженных) задач линейного программирования.
Для ряда практических задач линейного программирования целесообразно заменить решение исходной прямой задачи решением соответствующей двойственной задачи, симметричной исходной. Для любой прямой задачи линейного программирования можно сформулировать двойственную задачу следующим образом.
Составим двойственную задачу к задаче использования сырья.
Имеется m видов сырья в количестве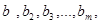 
которые используются для изготовления n видов продукции. Известно: 
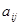- расход i-ого вида сырья на единицу j-ой продукции; 
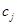- прибыль при реализации единицы j-ого вида продукции.
Математическая модель данной задачи имеет вид:
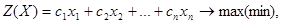(4.1.1)
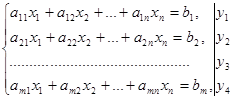(4.1.2)
xj ≥ 0, j = 1,2,…,n. (4.1.3)
Здесь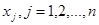 
- объем производства j-ого вида продукции.
Предположим, что второй производитель хочет перекупить сырье. Составим двойственную задачу, решение которой позволит определить условия продажи сырья. Введем вектор оценок (цен) видов сырья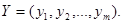 
Затраты на приобретение i-ого вида сырья в количестве 
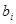равны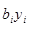 
. Второму производителю будет выгодно минимизировать суммарные затраты на приобретение всех видов сырья, поэтому целевая функция имеет вид:
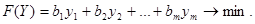(4.1.4)
Первому производителю невыгодно продавать сырье, если суммарная стоимость всех видов сырья, расходуемых на каждое изделие j-ой продукции, т.е.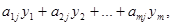 
Меньше прибыли 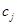, имеет вид:
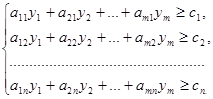(4.1.5)
Очевидно, что оценки видов сырья должны удовлетворять условиям неотрицательности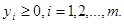 
(4.1.6)
Таким образом, связь исходной и двойственной задач состоит в том, что коэффициенты 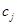целевой функции исходной задачи являются свободными членами системы ограничений двойственной задачи, свободные члены 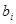системы ограничений исходной задачи служат коэффициентами целевой функции двойственной задачи, а матрица коэффициентов системы ограничений двойственной задачи является транспонированной матрицей коэффициентов системы ограничений двойственной задачи.
Рассмотренная пара задач относится к симметричным парам двойственных задач. В теории двойственности используются четыре пары двойственных задач (приведем их в матричной форме записи):
Исходная задача Двойственная задача
Симметричные пары
1. 
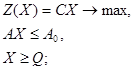
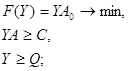(4.1.7)
2. 
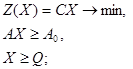
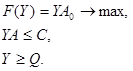(4.1.8)
Несимметричные пары
3. 
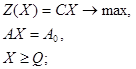
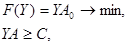(4.1.9)
4. 
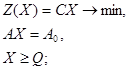
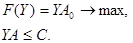(4.1.10)
Здесь 
