Задачи для контрольных заданий
1–10. Найти область определения заданных функций.
1. а) 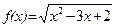 ; б)
; б) 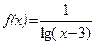 .
.
2. а) 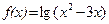 ; б)
; б) 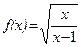 .
.
3. а) 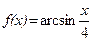 ; б)
; б) 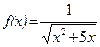 .
.
4. а) 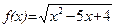 ; б)
; б) 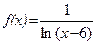 .
.
5. а) 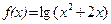 ; б)
; б) 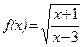 .
.
6. а) 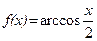 ; б)
; б) 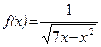 .
.
7. а) 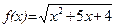 ; б).
; б). 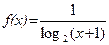 .
.
8. а) 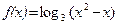 ; б)
; б) 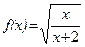 .
.
9. а) 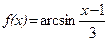 ; б)
; б) 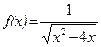 .
.
10. а) 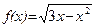 ; б)
; б) 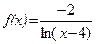 .
.
11–20.Построить графики функций.
11.а) 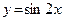 ; б)
; б) 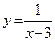 .
.
12. а) 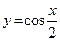 ; б)
; б) 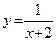 .
.
13. а) 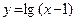 ; б)
; б) 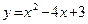 .
.
14. а) 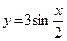 ; б)
; б) 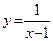 .
.
15. а) 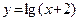 ; б)
; б) 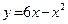 .
.
16. а) 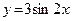 ; б)
; б) 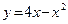 .
.
17. а) 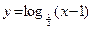 ; б)
; б) 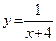 .
.
18. а) 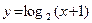 ; б)
; б) 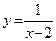 .
.
19. а) 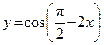 ; б)
; б) 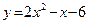 .
.
20. а) 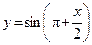 ; б)
; б) 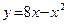 .
.
21–30.Изобразить схематично график функции y = f(x), удовлетворяющей заданным условиям.
21. 22.
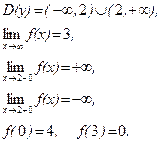
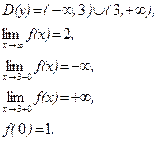
23. 24.
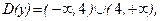
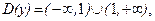
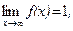
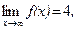
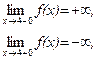
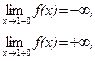
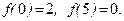
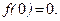
25. 26.
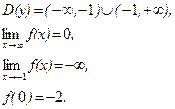
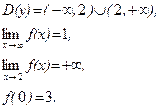
27. 28.
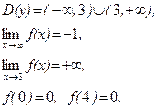
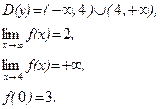
29. 30.
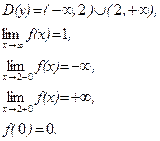
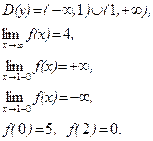
31–40. Найти пределы функций, не пользуясь правилом Лопиталя.
31.а) 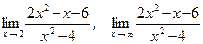 ;
;
б) 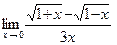 ; в)
; в) 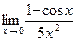 ;
;
г) 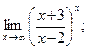 д)
д) 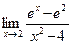 .
.
32.а) 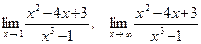 ;
;
б) 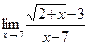 ; в)
; в) 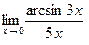 ;
;
г) 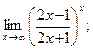 д)
д) 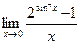 .
.
33.а) 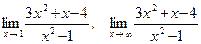 ;
;
б) 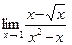 ; в)
; в) 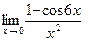 ;
;
г) 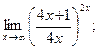 д)
д) 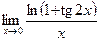 .
.
34.а) 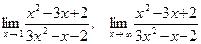 ;
;
б) 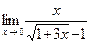 ; в)
; в) 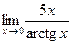 ;
;
г) 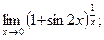 д)
д) 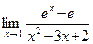 .
.
35.а) 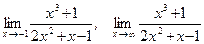 ;
;
б) 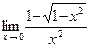 ; в)
; в) 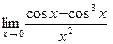 ;
;
г) 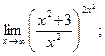 д)
д) 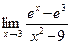 .
.
36.а) 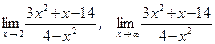 ;
;
б) 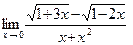 ; в)
; в) 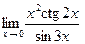 ;
;
г) 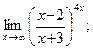 д)
д) 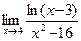 .
.
37.а) 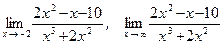 ;
;
б) 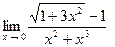 ; в)
; в) 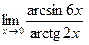 ;
;
г) 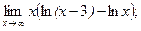 д)
д) 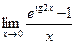 .
.
38.а) 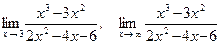 ;
;
б) 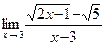 ; в)
; в) 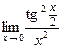 ;
;
г) 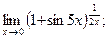 д)
д) 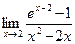 .
.
39.а) 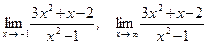 ;
;
б) 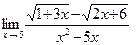 ; в)
; в) 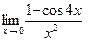 ;
;
г) 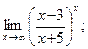 д)
д) 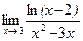 .
.
40.а) 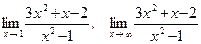 ;
;
б) 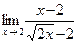 ; в)
; в) 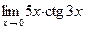 ;
;
г) 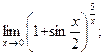 д)
д) 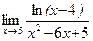 .
.
41–50. Заданы функции y=f(x). Требуется: определить их точки разрыва, характер точек разрыва и сделать схематический чертёж.
41. 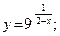
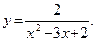
42. 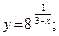
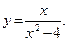
43. 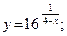
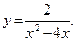
44. 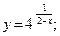
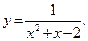
45. 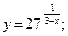
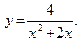
46. 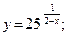
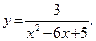
47. 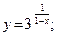
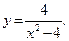
48. 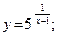
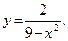
49. 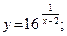
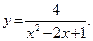
50. 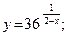
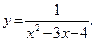
51–60.Найти точку разрыва функции y=f(x) и указать её характер. Построить график функции.
51. 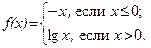
52. 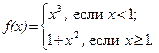
53. 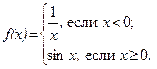
54. 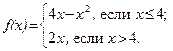
55. 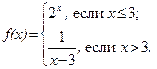
56. 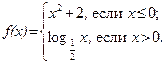
57. 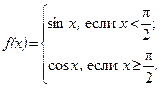
58. 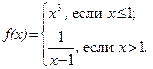
59. 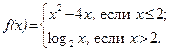
60. 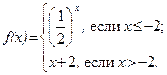
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Ниже приведена таблица номеров задач, входящих в задание на контрольную работу № 3. Студент должен выполнять контрольные задания по варианту, номер которого совпадает с последней цифрой его учебного номера (шифра).
| Вариант | ||||||||||
| Номера задач контрольных заданий | ||||||||||
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Письменный, Д.Т. Конспект лекций по высшей математике. Ч.1 / Д.Т. Письменный. – 2-е изд., исп. – М.: Айрис-пресс, 2003.
2. Лесняк, Л.И. Производная и ее приложения: учебное пособие / Л.И. Лесняк, В.А. Старенченко. – Томск: Изд-во НТЛ, 2005.
3. Бугров, Я.С. Дифференциальное и интегральное исчисление / Я.С. Бугров, С.М. Никольский. – М.: Наука, 1980.
4. Пискунов, Н.С. Дифференциальное и интегральное исчисление для втузов / Н.С. Пискунов. – М.: Наука, 1985. – Т. 1.
5. Берман, Г.И. Сборник задач по курсу математического анализа / Г.И. Берман. – М.: Наука, 1971.
ОГЛАВЛЕНИЕ
Введение…………………………………………………….. Введение в математический анализ………………...…... 1. Понятие функции……………………………………….. 1.1. В связи с чем возникло понятие функции?............... 1.2. Каким должен быть характер изменения двух переменных величин, чтобы одна из них являлась функцией другой?....................................................... 1.3. Как можно задать функцию?...................................... 1.4. Какие функции принято называть простейшими элементарными функциями?.........………………... 1.5. Графический обзор простейших элементарных функций……………………………………………... 1.6. Известен график функции y = f(x). Как построить графики функций y = f(x+a), y = f(x)+b, y = f(k ∙ x), y = k ∙ f(x) ?................................................ 1.7. Понятие сложной функции…………………………. 2. Понятие предела функции..…………………………… 2.1. Виды окрестностей. Условие принадлежности точки заданной окрестности………………………... 2.2. В связи с чем возникло понятие предела функции?. 2.3. Определение предела функции в случаях 1–4…….. 2.4. Определение односторонних пределов функции…. 3. Понятие непрерывности функции в точке………….. 3.1. Три определения непрерывной в точке x0 функции……………………………………………… 3.2. Геометрическая иллюстрация поведения функции в случаях…………………………………………….. 3.3. В каком случае функция y = f(x) называется непрерывной на замкнутом промежутке [a, b]?................ 3.4. В каком случае будут непрерывны функции 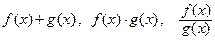 ?............................. 3.5. Что можно сказать о непрерывности простейших элементарных функций?............................................ 3.6. Перечислить условия, при которых сложная функция y = f(g(x)) будет непрерывна в точке x0 ... 3.7. Как много непрерывных функций?............................ 4. Техника вычисления пределов………….…...……….. 4.1. Как найти ?............................. 3.5. Что можно сказать о непрерывности простейших элементарных функций?............................................ 3.6. Перечислить условия, при которых сложная функция y = f(g(x)) будет непрерывна в точке x0 ... 3.7. Как много непрерывных функций?............................ 4. Техника вычисления пределов………….…...……….. 4.1. Как найти 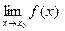 , если f(x) непрерывная в точке x0 функция?........................................................... 4.2. Как найти , если f(x) непрерывная в точке x0 функция?........................................................... 4.2. Как найти  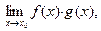 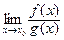 ? 4.3. Пусть ? 4.3. Пусть 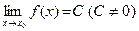 , , 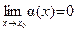 ( ( 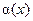 является бесконечно малой величиной при является бесконечно малой величиной при 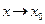 ), ), 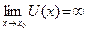 (U(x) является бесконечно большой величиной при (U(x) является бесконечно большой величиной при 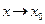 ). Перечислить теоремы, на основании которых ). Перечислить теоремы, на основании которых 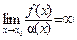 , , 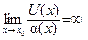 , , 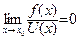 , , 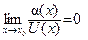 4.4. Что можно сказать о 4.4. Что можно сказать о 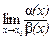 и и 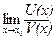 , где , где 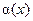 и и 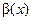 – бесконечно малые при – бесконечно малые при 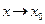 , U(x) и V(x) – бесконечно большие при , U(x) и V(x) – бесконечно большие при 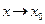 ?.............. 4.5. Что можно сказать о произведении бесконечно малой при ?.............. 4.5. Что можно сказать о произведении бесконечно малой при 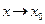 величине на ограниченную в окрестности точки x0 функцию?............................... 4.6. В каком случае произведение двух функций представляет собой неопределенное выражение?.............. 4.7. Что можно сказать о величине на ограниченную в окрестности точки x0 функцию?............................... 4.6. В каком случае произведение двух функций представляет собой неопределенное выражение?.............. 4.7. Что можно сказать о 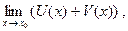 если U(x) и V(x) – бесконечно большие при x→x0 ?................... 4.8. Как найти предел степенно-показательной функции?...................................................................... 4.9. В каких случаях если U(x) и V(x) – бесконечно большие при x→x0 ?................... 4.8. Как найти предел степенно-показательной функции?...................................................................... 4.9. В каких случаях 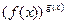 будет при x → x0 неопределенным выражением?................................. 4.10. На основании всего вышеизложенного перечислить все возможные неопределенные выражения…………………………………………………… Примеры на вычисление пределов функции………….. 1. Нахождение пределов в случае отсутствия неопределенности…………………………………………………... 2. Раскрытие неопределенностей вида будет при x → x0 неопределенным выражением?................................. 4.10. На основании всего вышеизложенного перечислить все возможные неопределенные выражения…………………………………………………… Примеры на вычисление пределов функции………….. 1. Нахождение пределов в случае отсутствия неопределенности…………………………………………………... 2. Раскрытие неопределенностей вида 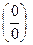 …………… 2.1. Нахождение …………… 2.1. Нахождение 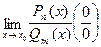 , где Pn(x) и Qm(x) некоторые многочлены, путем разложения числителя и знаменателя на множители…………………. 2.2. Раскрытие иррациональных неопределенностей вида , где Pn(x) и Qm(x) некоторые многочлены, путем разложения числителя и знаменателя на множители…………………. 2.2. Раскрытие иррациональных неопределенностей вида 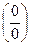 …………………………………………….. 2.3. Раскрытие неопределенных выражений вида …………………………………………….. 2.3. Раскрытие неопределенных выражений вида 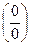 с помощью первого замечательного предела и его следствий……………………………………… 2.4. Введение новой переменной……………………... 3. Раскрытие неопределенностей вида с помощью первого замечательного предела и его следствий……………………………………… 2.4. Введение новой переменной……………………... 3. Раскрытие неопределенностей вида 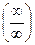 …………… 4. Раскрытие неопределенностей вида …………… 4. Раскрытие неопределенностей вида 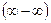 и и 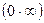 .. 5. Раскрытие неопределенностей вида .. 5. Раскрытие неопределенностей вида 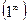 …………….. 6. Использование эквивалентностей при вычислении пределов………………………………………………..... 5. Классификация точек разрыва функции.................... 5.1. В чём заключается необходимое и достаточное условие непрерывности функции в точке x0 ?........ 5.2. Как осуществляется классификация точек разрыва функции?....................................................................... 5.3. Примеры на нахождение точек разрыва функции и их классификацию…………………………………... 6. Задачи для контрольных заданий.…………………… Контрольные задания…………………………………….. Список рекомендуемой литературы……………………. …………….. 6. Использование эквивалентностей при вычислении пределов………………………………………………..... 5. Классификация точек разрыва функции.................... 5.1. В чём заключается необходимое и достаточное условие непрерывности функции в точке x0 ?........ 5.2. Как осуществляется классификация точек разрыва функции?....................................................................... 5.3. Примеры на нахождение точек разрыва функции и их классификацию…………………………………... 6. Задачи для контрольных заданий.…………………… Контрольные задания…………………………………….. Список рекомендуемой литературы……………………. |
