Радиальная (круговая) СКП обсервованного места судна

Рис. 18.10. Погрешность обсервованного места судна

Поскольку обсервованное место судна образуется пересечением минимум двух линий положения, а, значит, и двух полос, то на путевой карте мы получим не точку С (рис. 18.10), а так называемую фигуру погрешностей «абсд». Размеры этой фигуры при неизменных m_ЛП будут зависеть, прежде всего, от угла пересечения линий положения – угла q.

При Ðq = 90° площадь фигуры погрешностей наименьшая, а при m_ЛП1 = m_ЛП2 – квадрат. Но, чем меньше будет этот Ðq, тем больше будет площадь фигуры погрешностей «абсд».

Вероятность нахождения обсервованного места судна в этой фигуре погрешностей равна произведению вероятностей нахождения места судна в каждой из полос, то есть: Р = 0,68 × 0,68 » 0,46 (46%).

Однако, точность места судна принято оценивать не параллелограммом «абсд» (ромбом, квадратом) погрешностей, а эллипсом, вписанным в этот параллелограмм (рис. 18.11).

Рис. 18.11. Эллиптическая погрешность обсервованного места судна

Эллипс погрешностей обладает следующими свойствами:

1. Размеры и ориентировка эллипса погрешностей дают наглядное представление о точности определения места по различным направлениям.
2. Вероятность того, что случайная погрешность не выйдет за пределы эллипса погрешностей больше, чем для любой другой фигуры погрешности, имеющей такую же площадь.
3. Среди всех фигур, в пределах которых, вероятность нахождения судна одинакова, эллипс погрешностей имеет наименьшую площадь.

Вероятность нахождения места судна в эллипсе погрешностей равна Р = 0,39(39%).

Но эллипс погрешностей, из-за сложности его построения, применяют только при решении специальных задач судовождения.

В повседневной практике используют более грубую, но более простую оценку точности места судна – через радиальную (круговую) СКП – М₀.

Радиальная (круговая) СКП обсервованного места (М₀) построена на полуосях эллипса погрешностей (рис. 18.12).

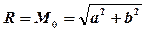, (18.18)

Вероятность нахождения обсервованного места судна в круге радиусом R = M₀ зависит от соотношения полуосей эллипса погрешностей.

Например: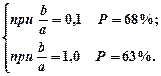

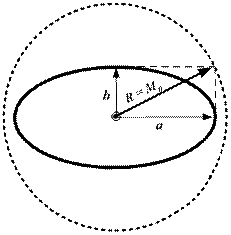
Рис. 18.12. Радиальная (круговая) СКП места судна

В общем случае, вероятность нахождения места судна в круге радиусом R = M₀ принимается равной 63% (0,63), так как в большинстве случаев соотношение полуосей эллипса b/a близко к 1.

Как видно из рис. 18.13 при q = 90°(sin q = 1) полуоси эллипса погрешностей численно равны по своей величине СКП линий положения (а = m_ЛП1, b = m_ЛП2) и формулу (18.18) для этого случая можно записать как:

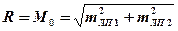, (18.19)

Для общего же случая (когда q ¹ 90°и sin q <1) радиальная (круговая) СКП обсервованного места судна M₀ в зависимости от СКП линий положения (m_ЛП1 и m_ЛП2) и угла их пересечения q определяется по общей формуле (18.20):

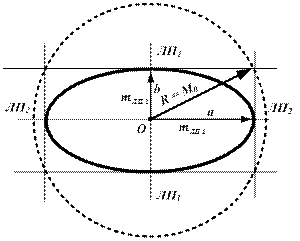
Рис. 18.13. Радиальная (круговая) СКП обсервованного места судна

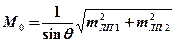, (18.20)

Эта формула является основной для расчета величины радиальной (круговой) СКП места судна, определенного по двум любым линиям положения.

При равноточных наблюдениях, то есть когда m_ЛП1 = m_ЛП2 формула (18.20) примет вид:

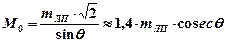, (18.21)

Решим задачу расчета M₀ на примере:

Дано: m_ЛП1 = ±2,5 мили; m_ЛП2 = ±1,0 мили; q = 43°; M₀ – ?

Решение: по формуле (18.20)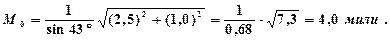

Если теперь из обсервованного места судна на путевой карте провести окружность радиусом R = M₀ = 4,0мили, то можно сказать, что фактическое место судна находится в пределах площади этой окружности с вероятностью Р = 63% (0,63).