Чему равны внутренние усилия и напряжения при внецентренном сжатии?


Пусть сжимающая сила 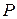 приложена в некоторой точке A с координатами
приложена в некоторой точке A с координатами  и
и  в главных центральных осях инерции x и y (см. рис. 10.1, а).
в главных центральных осях инерции x и y (см. рис. 10.1, а).
Тогда, с учетом принятого нами допущения,
 .
.
Точные значения изгибающих моментов определяются по формулам
 ,
,
где  и
и  – прогибы рассматриваемого поперечного сечения стержня в направлении осей
– прогибы рассматриваемого поперечного сечения стержня в направлении осей  и
и  соответственно. Принятое нами выше допущение о большой жесткости стержня на изгиб заключается в предположении, что
соответственно. Принятое нами выше допущение о большой жесткости стержня на изгиб заключается в предположении, что  .
.
Напряжения в произвольной точке  с координатами
с координатами  и
и  равны:
равны:
 , (10.1)
, (10.1)
где, согласно принципу независимости действия сил, первое слагаемое представляет собой напряжение от сжатия, а второе и третье – от изгиба.
Значения изгибающих моментов и координат исследуемой точки  подставляются в формулу (10.1) по абсолютному значению, а знак второго и третьего слагаемых определяется по физическому смыслу.
подставляются в формулу (10.1) по абсолютному значению, а знак второго и третьего слагаемых определяется по физическому смыслу.
10.2. Как определяется положение НЛ?
Преобразуем формулу (10.1), подставляя в нее значения изгибающих моментов:
 . (10.2)
. (10.2)
Обозначим координаты некоторой точки нулевой линии  и
и  . Подставим эти координаты в (10.2) вместо
. Подставим эти координаты в (10.2) вместо  и
и  соответственно, а также учтем, что напряжения в точках НЛ равны нулю. После сокращения на
соответственно, а также учтем, что напряжения в точках НЛ равны нулю. После сокращения на  получим уравнение НЛ:
получим уравнение НЛ:
 . (10.3)
. (10.3)
Таким образом, положение нулевой линии зависит от значений главных радиусов инерции поперечного сечения  ,
,  и координат точки приложения нагрузки
и координат точки приложения нагрузки  ,
,  и совершенно не зависит от величины силы P.
и совершенно не зависит от величины силы P.
Важно также отметить, что НЛ и точка приложения нагрузки всегда расположены по разные стороны от центра тяжести поперечного сечения (см. рис. 10.1, б).
10.3. Чему равны отрезки, отсекаемые НЛ от осей координат?
Эти отрезки, которые мы обозначим через  и
и  (см. рис. 10.1, б), легко найти из выражения (10.3). Если сначала в нем принять
(см. рис. 10.1, б), легко найти из выражения (10.3). Если сначала в нем принять  , а затем –
, а затем –  , то мы легко найдем, что отрезки, отсекаемые НЛ от осей координат, определяются по формулам
, то мы легко найдем, что отрезки, отсекаемые НЛ от осей координат, определяются по формулам
 ;
;  .
.
10.4. Что называется ядром сечения?

 Ядром сечения называется малая область вокруг центра тяжести поперечного сечения стержня. Она характеризуется тем, что всякая сжимающая сила, приложенная внутри этой области, вызывает во всех точках поперечного сечения (и соответственно во всем стержне) только напряжения сжатия.
Ядром сечения называется малая область вокруг центра тяжести поперечного сечения стержня. Она характеризуется тем, что всякая сжимающая сила, приложенная внутри этой области, вызывает во всех точках поперечного сечения (и соответственно во всем стержне) только напряжения сжатия.
Понятие о ядре сечения впервые ввел Бресс в 1854 г.
Рассмотрим следующий пример. Пусть стержень имеет прямоугольное поперечное сечение с размерами b и h и одна из координат точки приложения нагрузки (точка A) равна нулю, например  (рис. 10.2). Тогда напряжения в крайних точках K и L поперечного сечения стержня будут определяться по формулам
(рис. 10.2). Тогда напряжения в крайних точках K и L поперечного сечения стержня будут определяться по формулам

Из этих формул видно, что при  во всех точках поперечного сечения, в том числе и в крайних точках K и L,будут возникать одинаковые сжимающие напряжения. При
во всех точках поперечного сечения, в том числе и в крайних точках K и L,будут возникать одинаковые сжимающие напряжения. При  напряжения по-прежнему будут сжимающими, но будут изменяться по ширине сечения. При
напряжения по-прежнему будут сжимающими, но будут изменяться по ширине сечения. При  в точках K и L они будут равны:
в точках K и L они будут равны:  .
.
Если  , то НЛ разделит поперечное сечение на две части. В одной из них напряжения будут сжимающими, а в другой – растягивающими. Для всех этих случаев (см. рис. 10.2) показаны эпюры напряжений.
, то НЛ разделит поперечное сечение на две части. В одной из них напряжения будут сжимающими, а в другой – растягивающими. Для всех этих случаев (см. рис. 10.2) показаны эпюры напряжений.
Таким образом, если мы не хотим, чтобы в поперечном сечении внецентренно сжатого стержня возникали растягивающие напряжения (а многие строительные материалы, как известно, очень плохо работают на растяжение), то эксцентриситет нагрузки не должен выходить за некоторую область вокруг центра тяжести этого сечения. Эту область и называют ядром сечения.
