Экстремальные классы для распределенияплотности
Запись (1) оператора прямой задачи гравиметрии для распределения плотности не учитывает два важных с прикладной точки зрения обстоятельства. Во-первых, реально гравитационное поле задано на некоторой поверхности, а во-вторых, оно задано в дискретном, и более того, конечном наборе точек этого рельефа. Поэтому соотношение (1) должно быть обобщено соотношением:
 , (7.18)
, (7.18)
записываемом в той же самой операторной форме:

Здесь функция  ассоциируется с описанием рельефа, на котором задано поле
ассоциируется с описанием рельефа, на котором задано поле  Правая часть в (18) определена, либо для всех
Правая часть в (18) определена, либо для всех  либо для некоторого множества точек Г из
либо для некоторого множества точек Г из 
Для того чтобы подчеркнуть то обстоятельство, что в конкретной выкладке следует особо учитывать рельеф и способ задания поля, для (18) будем использовать запись
 . (7.19)
. (7.19)
Причем в (18) правая часть это еще не наблюдаемая, несмотря на то, что учтено и влияние рельефа, и конечность точек наблюдения. Неучтенными остаются множество факторов, таких как влияние масс вне области  , несовпадение вертикальной и нормальной производных и многое другое, требующее уточнения и операций редуцирования наблюдаемой к идеализированному соотношению (18). Легко увидеть, что если
, несовпадение вертикальной и нормальной производных и многое другое, требующее уточнения и операций редуцирования наблюдаемой к идеализированному соотношению (18). Легко увидеть, что если  , является однозначной функцией и область
, является однозначной функцией и область  целиком лежит в
целиком лежит в 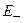 , то
, то
 .
.
Тогда, из теоремы 1, приведенной в 7.1 следует, что  , определенный соотношением (18) ограниченный оператор из
, определенный соотношением (18) ограниченный оператор из  в
в  для всех
для всех  если
если  ограничена, и для
ограничена, и для 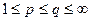 , если
, если  неограниченна. Обобщенным выражением для сопряженного к
неограниченна. Обобщенным выражением для сопряженного к  оператора
оператора  будет:
будет:
 (7.20)
(7.20)
где  есть мера на области задания
есть мера на области задания  Если
Если  задано для всех
задано для всех  то
то  и (20) трансформируется к аналогу (9):
и (20) трансформируется к аналогу (9):
 . (7.20-a)
. (7.20-a)
Если  задано в конечном множестве
задано в конечном множестве 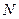 точек
точек  из
из  , то
, то  есть атомическая мера на
есть атомическая мера на  , и (20) примет вид:
, и (20) примет вид:
 (7.20-b)
(7.20-b)
где  - точки, в которых задано
- точки, в которых задано  .
.
Это следует из цепочки равенств, повторяющих с небольшими дополнениями (10):

Все эти соотношения объединяем записью (20).
Сопряженные операторы участвуют в конструкции идеальных и почти идеальных экстремальных классов (см. гл.5), доставляющих согласованную со способом задания поля конструкцию, на которых решение обратной задачи существует (существует с любой наперед заданной точностью для почти идеальных классов), единственно и осмысленно с точки зрения оптимальности уклонения от заданного элемента. Последнее обеспечивает содержательное и конструктивное применение метода минимальных корректив. Имея выражение для оператора  , сопряженного к
, сопряженного к  , легко получить выражение для почти идеальных экстремальных классов, введенных в 5.3. Напомним, что если оператор
, легко получить выражение для почти идеальных экстремальных классов, введенных в 5.3. Напомним, что если оператор 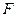 - линеен, имеет ограниченный обратный, и
- линеен, имеет ограниченный обратный, и  , то идеальный экстремальный класс в пространстве
, то идеальный экстремальный класс в пространстве 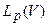 имеет вид:
имеет вид:
 . (7.21)
. (7.21)
Каждый элемент из ядра оператора (1) одновременно является и элементом ядра оператора (18). Это очевидное утверждение. Действительно, если распределение плотности таково, что гравитационное поле от него тождественно равно нулю всюду на 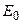 , и, как следствие, (в силу интеграла Пуассона) всюду в
, и, как следствие, (в силу интеграла Пуассона) всюду в 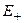 , то тем более оно равно нулю на любом конечном множестве точек из
, то тем более оно равно нулю на любом конечном множестве точек из 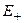 и любой поверхности в
и любой поверхности в 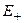 . (
. (  , где
, где  обозначает (18) в отличие от (1). Но, переходя к ортогональным дополнениям, которые связаны со значениями сопряженных операторов, тут же получаем
обозначает (18) в отличие от (1). Но, переходя к ортогональным дополнениям, которые связаны со значениями сопряженных операторов, тут же получаем
 .
.
Но это означает, что область значений сопряженного к  оператора
оператора  включает в себя все элементы из
включает в себя все элементы из  и, следовательно, экстремальные классы
и, следовательно, экстремальные классы  можно рассматривать одновременно как и элементы из
можно рассматривать одновременно как и элементы из  . Изучения свойств экстремальных классов, и, как следствие, свойств решений обратной задачи позволяет в дальнейших рассмотрениях обращаться в основном к случаю
. Изучения свойств экстремальных классов, и, как следствие, свойств решений обратной задачи позволяет в дальнейших рассмотрениях обращаться в основном к случаю  . Будем рассматривать поле
. Будем рассматривать поле  заданным, либо всюду на
заданным, либо всюду на  , либо в конечном множестве точек Г из
, либо в конечном множестве точек Г из  . Для того чтобы подчеркнуть это обстоятельство и, учитывая, что вид оператора прямой задачи фиксирован, для соответствующих экстремальных классов будем использовать обозначение
. Для того чтобы подчеркнуть это обстоятельство и, учитывая, что вид оператора прямой задачи фиксирован, для соответствующих экстремальных классов будем использовать обозначение  , либо
, либо  , а плотные в них подмножества, образующие почтиидеальные экстремальные классы, обозначаются
, а плотные в них подмножества, образующие почтиидеальные экстремальные классы, обозначаются  и
и  соответственно. Тогда:
соответственно. Тогда:
 ; (7.22)
; (7.22)
 . (7.23)
. (7.23)
Оператор проектирования на область 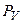 в выражениях (22,23) и им аналогичных можно опускать, в связи с тем очевидным обстоятельством, что изучаемые плотностные распределения рассматриваются только в пределах области
в выражениях (22,23) и им аналогичных можно опускать, в связи с тем очевидным обстоятельством, что изучаемые плотностные распределения рассматриваются только в пределах области  . Далее в силу того, что множество
. Далее в силу того, что множество  конечномерно и замыкание в конечномерном линейном пространстве совпадает с исходным пространством то
конечномерно и замыкание в конечномерном линейном пространстве совпадает с исходным пространством то  .
.
Далее примем, что если вместо символа  , либо
, либо  в выражении для экстремального класса, либо в другом предложении, где участвуют множества
в выражении для экстремального класса, либо в другом предложении, где участвуют множества  или
или  , стоит символ “*”, то формулируемое предложение в равной мере относится, как к случаю поля, заданного всюду в
, стоит символ “*”, то формулируемое предложение в равной мере относится, как к случаю поля, заданного всюду в  , так и к случаю, когда поле задано на множестве
, так и к случаю, когда поле задано на множестве  .
.
Определение 1.  (либо
(либо  ) – эквивалентным перераспределениемраспределения плотности
) – эквивалентным перераспределениемраспределения плотности  (*-эквивалентным) называется преобразование, оставляющее неизменным значение оператора
(*-эквивалентным) называется преобразование, оставляющее неизменным значение оператора  . В частности, неизменным
. В частности, неизменным  для всех
для всех  (либо
(либо  ).
).
Операции * - эквивалентного перераспределения можно дать определение с использованием операторной символики. Действительно, если обозначить (в соответствии с общими обозначениями из (3.2))  класс эквивалентности для элемента
класс эквивалентности для элемента  , совпадающий с классом смежности
, совпадающий с классом смежности  , введенным в разделе 7.1, то оператор *- эквивалентного перераспределения определен условием:
, введенным в разделе 7.1, то оператор *- эквивалентного перераспределения определен условием:
 есть оператор, в частности, оператор проектирования в норме пространства
есть оператор, в частности, оператор проектирования в норме пространства  , отображающий произвольное распределение плотности в элемент из своего класса эквивалентности.
, отображающий произвольное распределение плотности в элемент из своего класса эквивалентности.
В процедурах эквивалентного перераспределения важную роль играет различие между 
 – эквивалентным перераспределением. Поэтому для класса эквивалентности
– эквивалентным перераспределением. Поэтому для класса эквивалентности  введем уточняющее это обстоятельство обозначение
введем уточняющее это обстоятельство обозначение  и обозначение
и обозначение  для соответствующей операции
для соответствующей операции  , либо
, либо  эквивалентного перераспределения.
эквивалентного перераспределения.
Для операции эквивалентного перераспределенияиспользовано то же символическое обозначение, что и для операции проектирования. Это связано с тем, что любой оператор проектирования на класс эквивалентности, по определению является эквивалентным перераспределением. Поэтому роль индекса  в его определении играет вид нормы в соответствующем банаховом пространстве, в котором это проектирование осуществляется.
в его определении играет вид нормы в соответствующем банаховом пространстве, в котором это проектирование осуществляется.
Простейшей операцией эквивалентного перераспределения является добавление к распределению плотности элемента из ядра оператора  . (Ядра операторов
. (Ядра операторов 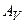 , в которых поле
, в которых поле  определено для
определено для  , либо для
, либо для  нетождественны). Другой, тривиальный пример эквивалентного перераспределения – тождественный оператор.
нетождественны). Другой, тривиальный пример эквивалентного перераспределения – тождественный оператор.
Прикладной смысл оператора эквивалентного перераспределения состоит в том, чтобы получить другое, эквивалентное по полю, но отличающееся по своим свойствам распределение. Например, в качестве такого свойства может выступать условие оптимальности вновь получаемого распределения. В этом случае необходимо иметь процедуру эквивалентного перераспределения, обеспечивающую принадлежность нового распределения плотности заданному экстремальному классу.
Теорема 6. Пусть 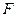 - линейный, взаимнооднозначный и взаимнонепрерывный оператор из
- линейный, взаимнооднозначный и взаимнонепрерывный оператор из  в
в  . Тогда оператор
. Тогда оператор
 . (7.24)
. (7.24)
является оператором  - эквивалентногоперераспределения на экстремальный класс
- эквивалентногоперераспределения на экстремальный класс  .
.
Доказательство. Обозначим  - образ
- образ  при отображении
при отображении 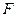 (это замкнутое подпространство в
(это замкнутое подпространство в  ). Тогда для
). Тогда для  имеем:
имеем:


где  Или:
Или:


Но: 
Откуда:


или, в силу теоремы о ядре:

что и доказывает требуемое.
Если  - сходящаяся минимизирующая последовательность:
- сходящаяся минимизирующая последовательность:

где  - монотонно возрастающая, непрерывная функция,
- монотонно возрастающая, непрерывная функция,  то, в силу непрерывности оператора
то, в силу непрерывности оператора  , имеем:
, имеем:

Следовательно, для любого  можно выбрать число
можно выбрать число  и соответствующий элемент
и соответствующий элемент  из последовательности
из последовательности  такой, что для всех
такой, что для всех 

Описанную процедуру численной минимизации можно рассматривать как процедуру 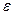 - эквивалентного перераспределения (т.е. эквивалентного с точностью
- эквивалентного перераспределения (т.е. эквивалентного с точностью 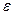 ).
).
Охарактеризуем теперь некоторые экстремальные классы.
Рассмотрим экстремальные классы, связанные с оператором Лапласа 
 .
.
Этот оператор весьма распространен в задачах математической физики и возникает не только как оператор уравнения:
 ,
,
которому удовлетворяют гармонические функции, но фактически во многих других уравнениях, в том числе и эволюционных, связанных с пространственным распределением некоторого параметра. Связано это с особым свойством симметрии для гармонических функций, которое проявляется в виде так называемой теореме о среднем. Ее суть состоит в том, что среднее значение по окружности или кругу соответствующей размерности (сфере, шару) для гармонической функции равно в точности ее значению в центре круга (шара). Их «веса» равны – среда в состоянии равновесия. Если оператор Лапласа от некоторой функции больше нуля, то среднее значение «перевешивает» значение в центре – больше его. Если значение оператора Лапласа от функции наоборот – меньше нуля, то среднее значение перевешивается значением в центре – оказывается «легче», чем значения в центре. Гармонические функции занимают особое место в математической физике. Точно также особое место в формулировках теорем единственности занимают экстремальные классы  , элементами которых служат гармонические функции.
, элементами которых служат гармонические функции.
Поскольку ядром оператора Лапласа являются гармонические области  функции, которые, как уже указывалось, ортогональны ядру оператора прямой задачи, имеем:
функции, которые, как уже указывалось, ортогональны ядру оператора прямой задачи, имеем:  Далее
Далее  - замкнутый оператор.
- замкнутый оператор.
Легко видеть, что  Действительно[30], функционал:
Действительно[30], функционал:

имеет минимум при  откуда следует, что
откуда следует, что  - гармоническая функция. Но
- гармоническая функция. Но  состоит из гармонических функций и является идеальным классом. Отсюда следует, что для каждого
состоит из гармонических функций и является идеальным классом. Отсюда следует, что для каждого  имеется решение задачи:
имеется решение задачи:

такое, что  и, следовательно,
и, следовательно, 
Легко получить из (21) выражение для почти идеальных экстремальных классов в пространстве  через выражения для
через выражения для  . Действительно, пользуясь (21) и подставляя (22) получаем для элементов из
. Действительно, пользуясь (21) и подставляя (22) получаем для элементов из  характеристику:
характеристику:

Рассмотрим далее, как выглядят экстремальные классы в Соболевских пространствах. С физической точки зрения эти рассмотрения эквивалентны решению вопроса о целесообразности введения в критерий оптимальности информации о гладкости искомого решения ОЗГ. Точнее, о целесообразности минимизации не только уклонения искомого решения от принятого нулевого приближения (которое, в частности, может быть и нулем), но и производных этого уклонения.
Теорема 7. Пусть  - замкнутая ограниченная область. Тогда
- замкнутая ограниченная область. Тогда  есть почти идеальное множество в
есть почти идеальное множество в 
Докажем предварительно следующий результат.
Лемма.  плотно в
плотно в  в метрике
в метрике  .
.
Доказательство леммы. Пространство  разлагается в сумму взаимноортогональных подпространств:
разлагается в сумму взаимноортогональных подпространств:  Кроме того,
Кроме того,  плотно в
плотно в  . Предположим, что утверждение леммы неверно. Тогда в
. Предположим, что утверждение леммы неверно. Тогда в  существует элемент
существует элемент  , и ни одна последовательность
, и ни одна последовательность  не сходится к
не сходится к  Но, поскольку сходящаяся последовательность из
Но, поскольку сходящаяся последовательность из  к
к  все же существует, то можно считать, что эта последовательность из
все же существует, то можно считать, что эта последовательность из  . Таким образом, получили последовательность
. Таким образом, получили последовательность  из
из  , сходящуюся к элементу из
, сходящуюся к элементу из  , что невозможно в силу взаимной ортогональности этих пространств.
, что невозможно в силу взаимной ортогональности этих пространств.
Доказательство теоремы. То, что  - почти идеальное множество, было доказано ранее. Необходимо показать включение:
- почти идеальное множество, было доказано ранее. Необходимо показать включение:

Рассмотрим задачу:
 (7.25.)
(7.25.)
Для ее решения  имеем необходимые и достаточные условия (см. прил.2.6):
имеем необходимые и достаточные условия (см. прил.2.6):


что в содержательных обозначениях приводит к:
 [31]
[31]  . (7.26)
. (7.26)
В соответствии с доказанной леммой условие  , участвующее в характеризации оптимального элемента, было заменено на:
, участвующее в характеризации оптимального элемента, было заменено на:  . Интегрируя (26) по частям:
. Интегрируя (26) по частям:

 .
.
По теореме о ядре:
 (7.27)
(7.27)
Таким образом, уравнение (27) характеризует класс  . Но если
. Но если  то и все производные любого порядка от этого распределения плотности также принадлежат этому множеству. Действительно, все производные гармонической функции – снова гармонические функции. Таким образом, множества распределений плотности
то и все производные любого порядка от этого распределения плотности также принадлежат этому множеству. Действительно, все производные гармонической функции – снова гармонические функции. Таким образом, множества распределений плотности  удовлетворяют (27) и, следовательно, являются решениями задачи (25). Требуемое включение
удовлетворяют (27) и, следовательно, являются решениями задачи (25). Требуемое включение  доказано.
доказано.
Из приведенного рассмотрения следует, что введение в критерий оптимальности дополнительных требований минимизации производных уклонения искомого решения от принятого нулевого приближения, не приводит к появлению в решении новых свойств и, следовательно, является излишним.
Рассмотрим вопрос о том, какие условия обеспечивают минимальность уклонения искомого решения от нуля в метрике 
Теорема 8. Знакопостоянные элементы из  принадлежат
принадлежат 
Доказательство. Прежде всего, ясно, что два знакопостоянных элемента из  имеют одинаковую величину нормы в
имеют одинаковую величину нормы в  . Это следует из того, что для знакопостоянных элементов величина:
. Это следует из того, что для знакопостоянных элементов величина:

с точностью до знака равна массе искомого распределения плотности и есть инвариант для  . Теперь покажем, что знакопостоянный элемент
. Теперь покажем, что знакопостоянный элемент  из
из  имеет меньшую величину нормы в
имеет меньшую величину нормы в  чем знакопеременный
чем знакопеременный  . Действительно, поскольку
. Действительно, поскольку  ,
, 
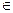
 , то их массы
, то их массы  равны, и:
равны, и:

Здесь:

Теорема доказана.
Знакопостоянные элементы образуют экстремальный класс  однако этот класс не является классом единственности. Рассмотрим эти вопросы подробней
однако этот класс не является классом единственности. Рассмотрим эти вопросы подробней
С этой целью рассмотрим задачу:
 (7.28)
(7.28)
решение которой существует в силу замкнутости  в метрике
в метрике 
Пусть область  будучи заполнена массами постоянной плотности
будучи заполнена массами постоянной плотности  создает вертикальную производную гравитационного потенциала
создает вертикальную производную гравитационного потенциала  Тогда для любого иного распределения плотности
Тогда для любого иного распределения плотности 

Действительно, если  и
и  - эквивалентны, то равны и их суммарные массы, а это означает, что
- эквивалентны, то равны и их суммарные массы, а это означает, что

Следовательно,  - знакопеременно, и существуют как точка
- знакопеременно, и существуют как точка  где
где  так и точка
так и точка  где
где  Но тогда:
Но тогда: 
Приведенным частным случаем исчерпываются ситуации, когда решение задачи (14) единственно. В частности, справедлив такой результат.
Если  не содержит элемента
не содержит элемента  то множество решений задачи (28) замкнуто, выпукло и содержит более одного элемента.
то множество решений задачи (28) замкнуто, выпукло и содержит более одного элемента.
Замкнутость и выпуклость следуют из ограниченности и линейности оператора (1). Что касается существования более чем одного решения, если есть решение (28) отличное от  то это следует из существования распределений плотности с как угодно малым носителем и как угодно малыми значениями, гравитационное поле от которых тождественно равно нулю. Такие примеры доставляют, в частности, вложенные шары равной, но противоположной как угодно малой массы, с плотностью непрерывно радиально меняющейся от центра к границе. К переменному - исходному решению задачи (28) всегда можно добавить такое финитное распределение, не изменив минимального значения его верхней грани. Выполнить это можно многими способами (в разных подобластях) и тем самым, исходя из заданного, будут построены новые и новые решения задачи (28). Важно, чтобы была хотя бы одна нетождественная константа – функция координат.
то это следует из существования распределений плотности с как угодно малым носителем и как угодно малыми значениями, гравитационное поле от которых тождественно равно нулю. Такие примеры доставляют, в частности, вложенные шары равной, но противоположной как угодно малой массы, с плотностью непрерывно радиально меняющейся от центра к границе. К переменному - исходному решению задачи (28) всегда можно добавить такое финитное распределение, не изменив минимального значения его верхней грани. Выполнить это можно многими способами (в разных подобластях) и тем самым, исходя из заданного, будут построены новые и новые решения задачи (28). Важно, чтобы была хотя бы одна нетождественная константа – функция координат.
Обратим внимание на то, что, как следует из приведенных выше рассмотрений, объект, занимающий область  и имеющий постоянную плотность
и имеющий постоянную плотность  минимально уклоняется от нуля во всех нормах
минимально уклоняется от нуля во всех нормах  в своем классе эквивалентности.
в своем классе эквивалентности.
Рассмотрим теперь классырешений обратной задачи гравиметрии, наименее уклоняющихся от нуля в равномерной метрике. Точнее, в соответствии с принятыми обозначениями – классы  Примем в качестве области
Примем в качестве области  уже использованную ранее горизонтальную полосу:
уже использованную ранее горизонтальную полосу:  а в качестве оператора
а в качестве оператора  - оператор свертки по горизонтальным координатам с функцией
- оператор свертки по горизонтальным координатам с функцией  аналитические свойства которой будут уточняться и определяться ниже, по мере возникающей в этом необходимости. Основой является задача:
аналитические свойства которой будут уточняться и определяться ниже, по мере возникающей в этом необходимости. Основой является задача:
 (7.29)
(7.29)
Замена переменных (в предположении существования оператора  ) трансформирует (29) к виду:
) трансформирует (29) к виду:
 (7.30)
(7.30)
Обобщенный аналог этой задачи рассматривался в п.5.4. В дальнейшем операция свертки двух функций  и
и  по горизонтальным координатам обозначается
по горизонтальным координатам обозначается 

 :
:

Введя функцию:

оператор прямой задачи в (29) перепишется:
 (7.31)
(7.31)
Это справедливо только в том случае, если в качестве носителя масс  выступает горизонтальная полоса
выступает горизонтальная полоса 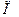 , что и предполагается всюду далее.
, что и предполагается всюду далее.
Легко убедиться в том, что для любой функции 

Пусть теперь оператор  входящий в (29) и (30) таков, что существует функция
входящий в (29) и (30) таков, что существует функция  и:
и:
 (7.32)
(7.32)
где:  - положительна, оператор
- положительна, оператор 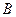 - линеен и ограничен из
- линеен и ограничен из 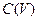 в
в  а его ядро не содержит функций, не зависящих от вертикальной координаты. Кроме того, считаем, что ядро сопряженного в
а его ядро не содержит функций, не зависящих от вертикальной координаты. Кроме того, считаем, что ядро сопряженного в 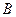 оператора содержит только ноль. Это значит, что множество его значений образует плотное в
оператора содержит только ноль. Это значит, что множество его значений образует плотное в  множество. Задача (32) полностью эквивалентна (5.46) с точностью до обозначений (там вместо
множество. Задача (32) полностью эквивалентна (5.46) с точностью до обозначений (там вместо  участвует
участвует  ). В этом случае к задаче (30) можно применить результаты из п. 5.4, в соответствии с которыми экстремальный класс
). В этом случае к задаче (30) можно применить результаты из п. 5.4, в соответствии с которыми экстремальный класс  состоит из распределений плотности
состоит из распределений плотности  в
в  представимых в виде:
представимых в виде:
 (7.33)
(7.33)
где:  - независящая от вертикальной координаты
- независящая от вертикальной координаты 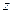 функция из
функция из  .
.
Перейдем к рассмотрению некоторых частных случаев. Пусть  положительная и непрерывная в интервале
положительная и непрерывная в интервале  функция. Легко убедиться в том, что если применять в качестве функций
функция. Легко убедиться в том, что если применять в качестве функций  в (32)
в (32)  то оператор
то оператор 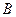 удовлетворяет требуемым свойствам. Оператор
удовлетворяет требуемым свойствам. Оператор 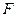 , определяющий критерий оптимальности в (29), состоит в делении распределения плотности на функцию
, определяющий критерий оптимальности в (29), состоит в делении распределения плотности на функцию  . Экстремальный класс
. Экстремальный класс  в этом случае состоит из распределений плотности представимых в виде функции с «разделяющимися» переменными
в этом случае состоит из распределений плотности представимых в виде функции с «разделяющимися» переменными  Для определения функции
Для определения функции  имеем уравнение:
имеем уравнение:

Предполагая, что  применим к последнему равенству преобразование Фурье по переменным
применим к последнему равенству преобразование Фурье по переменным  После элементарных вычислений получим:
После элементарных вычислений получим:

где  Напомним, что преобразование Фурье функции
Напомним, что преобразование Фурье функции  обозначается
обозначается  или
или  Для обратного преобразования Фурье функции
Для обратного преобразования Фурье функции  используется обозначение
используется обозначение  или
или 
Для решения  из
из  получаем выражение в виде неограниченного оператора:
получаем выражение в виде неограниченного оператора:
 . (7.34)
. (7.34)
В силу результатов п.5.3, его область определения плотна в  . Решение, доставляемое соотношением (34), как уже указывалось выше, оптимально в своем классе эквивалентности относительно критерия:
. Решение, доставляемое соотношением (34), как уже указывалось выше, оптимально в своем классе эквивалентности относительно критерия:
 (7.35)
(7.35)
Легко заметить, что заданием функции  предопределен закон изменения плотности в вертикальном направлении. Таким образом, если известно, как меняется плотность в вертикальном направлении, и это изменение -
предопределен закон изменения плотности в вертикальном направлении. Таким образом, если известно, как меняется плотность в вертикальном направлении, и это изменение -  сохраняется в пределах пласта, то такая информация выражается в критерии оптимальности (35), а решение получается по формуле (34). В частном случае, если
сохраняется в пределах пласта, то такая информация выражается в критерии оптимальности (35), а решение получается по формуле (34). В частном случае, если  , получаем из (34) решение В.М. Новоселицкого:
, получаем из (34) решение В.М. Новоселицкого:
 (7.36)
(7.36)
Наглядное представление о том, как влияет выбор функции  на получаемое по формуле (21) решение, можно получить из серии рисунков 2 На них представлены эквивалентные решения, а вид соответствующей функции
на получаемое по формуле (21) решение, можно получить из серии рисунков 2 На них представлены эквивалентные решения, а вид соответствующей функции  помещен непосредственно под рисунком.
помещен непосредственно под рисунком.
 |  | |
 |  | |
Продолжим далее по аналогии.
Если  - заданная функция трех пространственных переменных, то определим оператор
- заданная функция трех пространственных переменных, то определим оператор  так, что:
так, что:
| Рисунок 7.2 Эквивалентные решения |

Решение обратной задачи будем искать в виде:
 (7.37)
(7.37)
Подставляя последнее выражение в (31):

Выполняя преобразование Фурье:
 , откуда получаем:
, откуда получаем:
 (7.38)
(7.38)
