Интегрирование некоторых иррациональных функций интегралы от квадратичных иррациональностей (10)
Интегралы вида: 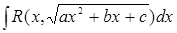 , где R- рациональная дробь по
, где R- рациональная дробь по 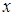 и
и 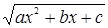 . Здесь
. Здесь 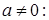
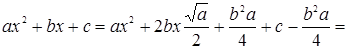
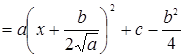 производим замену (
производим замену ( 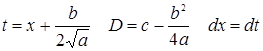 ):
): 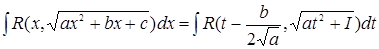
а).a>0 и D>0 т. е. 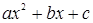 не имеет действительных корней, тогда:
не имеет действительных корней, тогда: 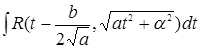 рационализируются т. е. сводится к интегралу от рациональной дроби подстановкой
рационализируются т. е. сводится к интегралу от рациональной дроби подстановкой 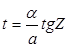 :
: 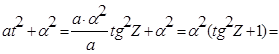
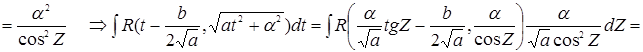
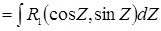 т. е. рационализируются.
т. е. рационализируются.
б.a>0 и D<0 т. е. 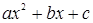 имеет действительные корни. В этом случае
имеет действительные корни. В этом случае 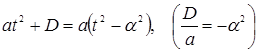 и рационализируются интеграл подстановкой
и рационализируются интеграл подстановкой 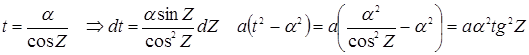
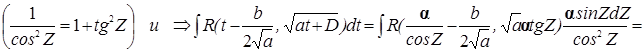
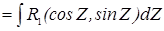 т. е. рационализируется.
т. е. рационализируется.
в.a<0 и D>0 тогда at2+D=α2-t2 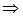 рационализируются подстановкой: t=αcosZ и t=αsinZ
рационализируются подстановкой: t=αcosZ и t=αsinZ
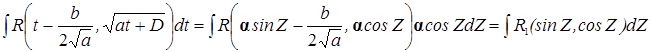
т. е. рационализируется.
Замечание:Кроме указанных тригонометрических подстановок могут использоваться и другие подстановки, а именно гиперболические.
а.a>0 и D>0 Используем подстановку 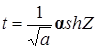 получаем:
получаем:
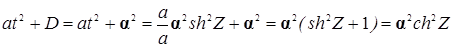 (т. к.
(т. к. 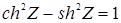 )
)
б.a>0 и D<0 Используем подстановку 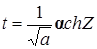 получаем:
получаем:
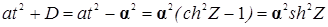 . В этом случае лучше всего делать тригонометрические подстановки: t=αcosZ и t=αsinZ
. В этом случае лучше всего делать тригонометрические подстановки: t=αcosZ и t=αsinZ
Замечание № 2:Кроме тригонометрических подстановок используют: 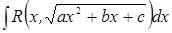 используют подстановки Эллера (1,2,3 подстановки).
используют подстановки Эллера (1,2,3 подстановки).
1 подстановка Эллера:Если a>0, то делают подстановку 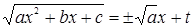
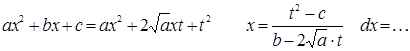
2 подстановка Эллера:c>0, тогда 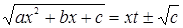
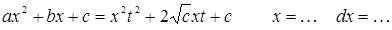
3 подстановка Эллера:Если 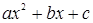 имеет действительные корни α и β то делают подстановку
имеет действительные корни α и β то делают подстановку 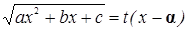 или
или 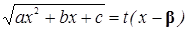 и находят x и dx.
и находят x и dx.
Замечание № 3:Существуют и другие классы интегралов от рациональных функций которые не всегда рационализируется а выражение в виде специальных функций к ним относятся эллиптические интегралы.
Определенный интеграл и его свойства (11)
Пусть функция f(x) определена и непрерывна на [a,b] разобьем отрезок [a,b] точками x0=a, x1 …, xn=b на n частичных отрезков [xi-1, xi], i=1,…,n, обозначим через 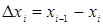 длинна отрезка на каждом отрезков [xi-1, xi] выберем произвольно
длинна отрезка на каждом отрезков [xi-1, xi] выберем произвольно 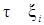 составим сумму
составим сумму 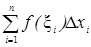 и назовем интегральной суммой для функции f(x) на [a,b].
и назовем интегральной суммой для функции f(x) на [a,b].
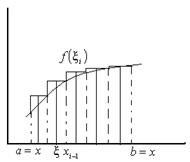
Площадь этой ступенчатой фигуры равна 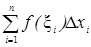 . Так как f(x)-непрерывная функция на отрезке [a,b] то она и ограничена на [a,b] следовательно она ограничена и на каждом отрезке [xi-1, xi] т.е. существует mi, Mi, что
. Так как f(x)-непрерывная функция на отрезке [a,b] то она и ограничена на [a,b] следовательно она ограничена и на каждом отрезке [xi-1, xi] т.е. существует mi, Mi, что 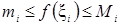 для i=1,…, n следовательно
для i=1,…, n следовательно 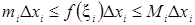 при
при 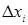 >0, а следовательно
>0, а следовательно 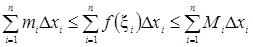 (
( 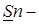 нижняя интегральная сумма,
нижняя интегральная сумма, 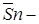 верхняя интегральная сумма). Опр. Если существует предел интегральных сумм
верхняя интегральная сумма). Опр. Если существует предел интегральных сумм 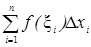 , когда
, когда 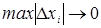 то этот предел называется определенным интегралом от функции f(x) на отрезке [a,b] и образует
то этот предел называется определенным интегралом от функции f(x) на отрезке [a,b] и образует 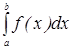 .
.
Итак по определению 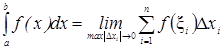 и этот предел не зависит как от способа разбиения отрезка [a,b] точкой xi на частичные отрезки [xi-1, xi], так и от выбора точек
и этот предел не зависит как от способа разбиения отрезка [a,b] точкой xi на частичные отрезки [xi-1, xi], так и от выбора точек 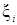 в них.
в них.
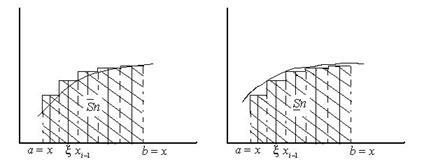
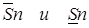 частные случаи интегральной суммы
частные случаи интегральной суммы 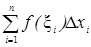 . Численно при
. Численно при 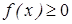 на [a,b]
на [a,b] 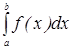 равен площади криволинейной трапеции ограниченной снизу осью абсцисс, сверху кривой f(x) с право кривой x=b, слева кривой x=b.
равен площади криволинейной трапеции ограниченной снизу осью абсцисс, сверху кривой f(x) с право кривой x=b, слева кривой x=b.
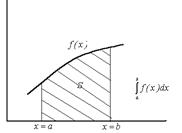
Геометрический смысл определенного интеграла – площадь кривой трапеции.
