Бесконечномерный случай
Описанные выше приемы, относящиеся к конечномерному случаю, могут быть распространены на бесконечномерный. Следующие результаты, приводящиеся без доказательств, характеризуют метод М.М. Лаврентьева решения неустойчивых задач. Ограничением применимости метода служит условия положительности( 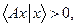 при
при 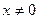 ) и самосопряженности (
) и самосопряженности ( 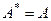 ). Доказательство приводится в [ 3, стр.63].
). Доказательство приводится в [ 3, стр.63].
Пусть А, 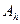 - линейные самосопряженные положительные операторы, действующие на гильбертовом пространстве Х.
- линейные самосопряженные положительные операторы, действующие на гильбертовом пространстве Х. 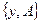 и
и 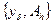 , соответственно, - точные и приближенные данные задачи (7) а
, соответственно, - точные и приближенные данные задачи (7) а 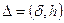 - ошибка данных. Пусть
- ошибка данных. Пусть  существует (т.е. А - взаимно-однозначно). Тогда уравнение
существует (т.е. А - взаимно-однозначно). Тогда уравнение
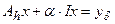 , (4.12)
, (4.12)
где 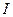 - единичный оператор, разрешимо для любых
- единичный оператор, разрешимо для любых 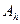 ,
, 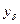 ,
, 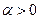 и его решение -
и его решение - 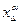 сходится к решению задачи (7) с точными данными при связи
сходится к решению задачи (7) с точными данными при связи 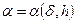 и
и  такой, что:
такой, что:
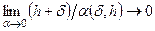 . (4.13)
. (4.13)
Таким образом, семейство операторов:
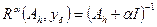 ,
,
параметризованное числом  , для которого выполняется требование (13), есть регуляризирующее семейство, а
, для которого выполняется требование (13), есть регуляризирующее семейство, а 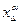 - регуляризированное семейство приближенных решений. Параметр
- регуляризированное семейство приближенных решений. Параметр 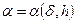 называется параметром регуляризации. Выбор величины параметра регуляризации
называется параметром регуляризации. Выбор величины параметра регуляризации  по правилу (13) объясняется следующим неравенством:
по правилу (13) объясняется следующим неравенством:
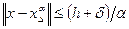
так что при 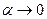 имеем
имеем 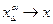 .
.
При отсутствии ошибок в операторе 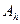 Метод М.М. Лаврентьевапри некоторых дополнительных условиях оказывается оптимальным по порядку на множестве
Метод М.М. Лаврентьевапри некоторых дополнительных условиях оказывается оптимальным по порядку на множестве 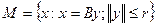 , где В - линеен, ограничен, действует из X в X. В том случае, когда в операторе имеются погрешности и используется
, где В - линеен, ограничен, действует из X в X. В том случае, когда в операторе имеются погрешности и используется 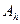 необходимо вводить двухсторонние оценки для возникающих погрешностей при использовании процедуры регуляризации по Лаврентьеву [2 стр.141]. Если множество М как и выше имеет вид
необходимо вводить двухсторонние оценки для возникающих погрешностей при использовании процедуры регуляризации по Лаврентьеву [2 стр.141]. Если множество М как и выше имеет вид 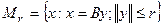 , но оператор B дополнительно коммутирует как с А, так и
, но оператор B дополнительно коммутирует как с А, так и 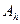 , то двухсторонняя оценка погрешности
, то двухсторонняя оценка погрешности 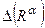 для метода Лаврентьева выражается через модуль непрерывности обратного к
для метода Лаврентьева выражается через модуль непрерывности обратного к  оператора на подмножестве в
оператора на подмножестве в 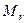 с условием невязки
с условием невязки 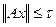 :
: 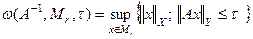 [16][3.стр.139].
[16][3.стр.139].
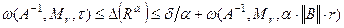 | (4.14) |
Обобщением на бесконечномерный случай первого из описанных выше приемов регуляризации задачи для матрицы требует введение понятия разложения единицы 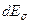 для самосопряженного положительного оператора
для самосопряженного положительного оператора 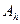 - со спектром, целиком заполняющим отрезок
- со спектром, целиком заполняющим отрезок 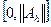 . Это аналог системы собственных функций, образующих собственные подпространства так, что
. Это аналог системы собственных функций, образующих собственные подпространства так, что 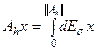 и функция
и функция 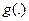 от оператора считается по формуле
от оператора считается по формуле 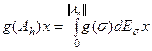 . В этом случае аналогом соотношения (9), определяющего регуляризованный оператор служит:
. В этом случае аналогом соотношения (9), определяющего регуляризованный оператор служит:
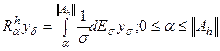 . (3.14)
. (3.14)
 - разложение единицы, порожденное оператором
- разложение единицы, порожденное оператором 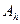 .
.
Если 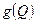 - строго возрастающая, непрерывная и равная нулю в нуле функция,
- строго возрастающая, непрерывная и равная нулю в нуле функция, 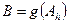
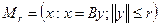 ,
,
и  подчинено условию:
подчинено условию:
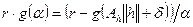 , то (14) – семейство регуляризующих операторов.
, то (14) – семейство регуляризующих операторов.
Описанные подходы требуют самосопряженности и положительности оператор 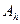 . Если указанное условие не выполнено, то можно перейти к уравнению с самосопряженным положительным оператором путем умножения оператора
. Если указанное условие не выполнено, то можно перейти к уравнению с самосопряженным положительным оператором путем умножения оператора 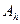 на сопряженный -
на сопряженный - 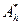 :
:
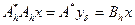 .
.
Оператор 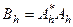 уже удовлетворяет требуемым условиям. Однако такой путь имеет тот недостаток, что для неустойчивой задачи домножение оператора на сопряженный приводит к еще большему ухудшению свойств устойчивости. Это происходит потому, что при умножении операторов их собственные числа умножаются, и малое собственное число после умножения само на себя становиться еще меньше. Таким образом, при умножении оператора на свой сопряженный на первом этапе свойства устойчивости еще более ухудшаются, а лишь далее положение исправляется. Такой путь следует применять тогда, когда свойства оператора не допускают применение иных алгоритмов регуляризации.
уже удовлетворяет требуемым условиям. Однако такой путь имеет тот недостаток, что для неустойчивой задачи домножение оператора на сопряженный приводит к еще большему ухудшению свойств устойчивости. Это происходит потому, что при умножении операторов их собственные числа умножаются, и малое собственное число после умножения само на себя становиться еще меньше. Таким образом, при умножении оператора на свой сопряженный на первом этапе свойства устойчивости еще более ухудшаются, а лишь далее положение исправляется. Такой путь следует применять тогда, когда свойства оператора не допускают применение иных алгоритмов регуляризации.
