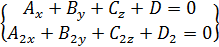Свойство скалярного Скалярное
1) 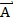 *
* 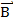 =
= 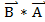
2)( 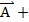
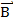 )*
)* 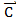 =
= 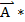
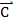 +
+ 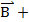
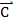
3)( 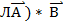 =
= 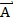 (
( 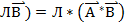 Л- число
Л- число
4) 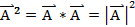
5) 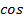 (
( 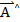
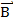 )=
)= 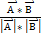
6)Если 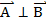 , то
, то 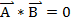
16 Векторное произведение векторов: определение, свойства, вычисление в координатной форме.
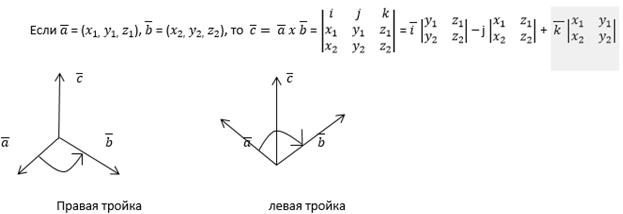
Векторным произведением векторов 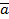 и
и 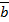 называется вектор
называется вектор 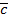 , для которого выполняются условия:
, для которого выполняются условия:
1) 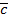
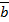
2) Вектора 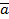 ,
, 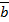 ,
, 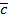 - образуют правую тройку
- образуют правую тройку
3) 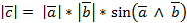 или
или 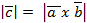
Обозначение  , или [
, или [  ]
]
Свойства векторного произведения
1) 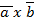 = - (
= - ( 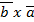 )
)
2) ( 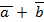 ) x
) x 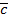 =
= 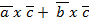
3) (λ 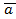 ) x
) x 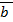 =
= 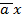 (λ
(λ 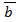 ) = λ(
) = λ( 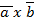 )
)
4) 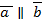 < = >
< = > 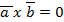
5) 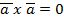
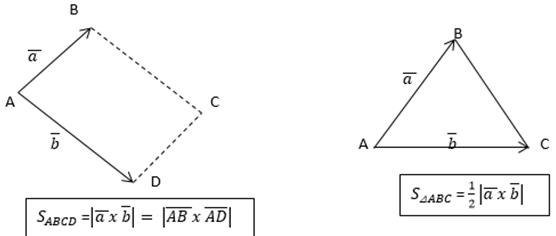
6) Геометрический смысл
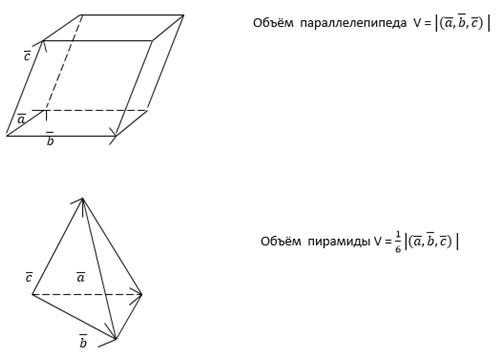
17 Смешанное произведение векторов: определение, свойства, вычисление в координатной форме.
Смешанным произведением векторов  ,
,  ,
, 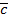 называется вектор полученный путем скалярного умножения векторов
называется вектор полученный путем скалярного умножения векторов 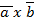 на
на 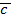
Обозначается: ( 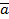 ,
, 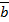 ,
, 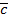 ) = (
) = ( 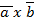 )*
)* 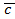
Свойства:
1) ( 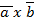 )*
)* 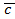 = (
= ( 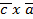 )*
)* 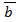 = (
= ( 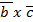 )*
)* 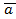
2) ( 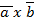 )*
)* 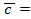
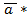 (
( 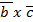 )
)
3) 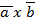 *
* 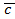 = -
= - 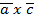 *
* 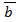
4) 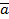 ,
, 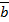 ,
, 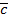 - комплонарны (если лежат в одной плоскости) тогда и только, тогда и когда (
- комплонарны (если лежат в одной плоскости) тогда и только, тогда и когда ( 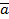 ,
, 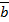 ,
, 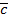 ) = 0
) = 0
5) Если ( 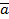 ,
, 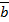 ,
, 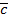 ) > 0, то
) > 0, то 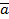 ,
, 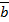 ,
, 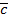 – правая тройка
– правая тройка
( 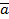 ,
, 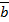 ,
, 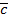 ) < 0, то
) < 0, то 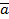 ,
, 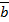 ,
, 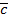 – левая тройка
– левая тройка
6) Если 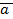 = (
= ( 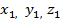 ),
), 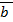 = (
= ( 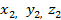 ),
), 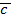 = (
= ( 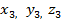 )
)
( 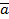 ,
, 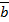 ,
, 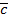 ) =
) = 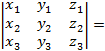
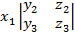 –
– 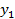
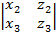 +
+ 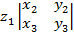
18 Билет Ризличные виды уравнений прямой на плоскости. Взаимное расположение прямых, угол между прямыми, расстояние от точки до прямой.
Уравнение вида: Ax+By+C=0 называется общим уравнением прямой.
В зависимости от того какими условиями задается прямая уравнения прямой будет иметь разный вид.
Обозначения

Уравнение прямой
1) Если известен нормальный вектор 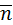 =(A, B) и точка
=(A, B) и точка 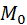 (
( 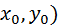 через которую проходит прямая ι
через которую проходит прямая ι
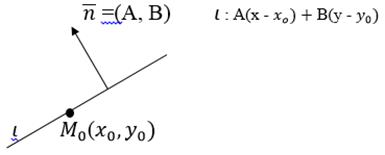
2) Уравнение прямой векторах. Если прямая ι отсекает от оси OX отрезок a, от оси OY отрезок b, то ее управление имеет вид:
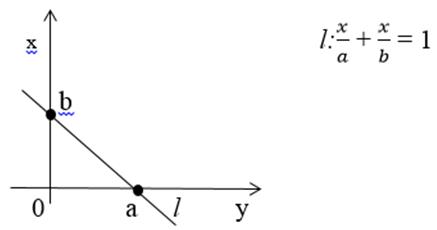
3) Каноническое уравнение прямой. Если известен направляющий вектор 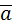 =(l, m) и точка
=(l, m) и точка 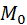 (
( 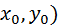 , то уравнение прямой l:
, то уравнение прямой l:
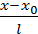 =
= 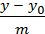
4) Параметрическое уравнение прямой (получается из канонического)
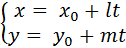 параметр - t
параметр - t
5) Если известны 2 точки через которые проходит прямая l 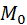 (
( 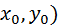 и
и
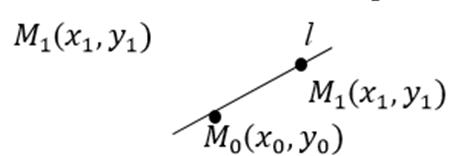
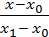 =
= 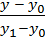
6) 
 Если известен угловой коэффициент k = tg
Если известен угловой коэффициент k = tg 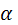 и точка
и точка 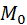 (
( 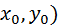 через которую проходит прямая l :
через которую проходит прямая l :
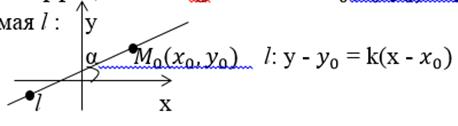
Расстояние от точки 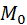 (
( 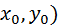 до прямой l: Ax+By+C=0
до прямой l: Ax+By+C=0
d = 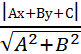
Взаимное положение прямых 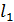 и
и 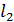
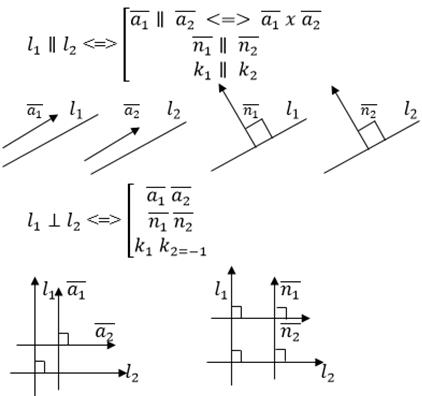
Угол между прямыми 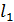 и
и 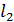
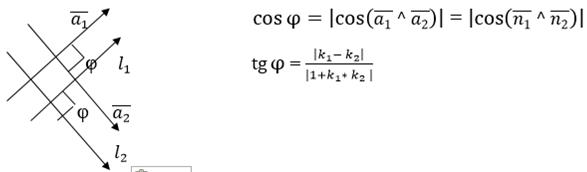
20.Уравнение плоскости в пространстве. Взаимно расположенные плоскости. Угол между плоскостями.Расстояние от точки до плоскости.
1) Определение: Уравнение: Ax+By+Cz+D=0 называется общим уравнением плоскости в пространства
Обозначения:
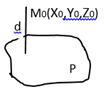
P: M(x,y)
M(x,y)-точка на плоскости P
1.Если дана точка M0(X0,Y0,Z0) и 2 некомисарных вектора ā1=(K1,L1,M1) и ā2=(K2,L2,M2)

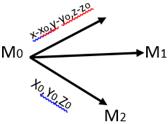
2.Если известны 3 точки через которые проходит плоскость M0(X0,Y0,Z0), M1(X1,Y1,Z1) и M2(X2,Y2,Z2)

3. Уравнение плоскости в отрезках
P:=  +
+  +
+  =1
=1
4.Если задан нормальный вектор =(A,B,C) и точка M0(X0,Y0,Z0), через которую проходят плоскость P: A(x-x0)+B(y-y0)+C(z-z0)=0
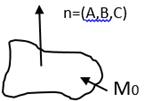
2)
3) Cos(P1^P2)=|cos n1 ^ n2|= 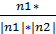
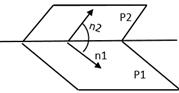
4) P:Ay+By+Cz+D=0
d= 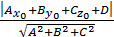
21.Уравнение прямой в пространстве.
L-прямая, уравнение которой следует написать, M(x,y,z)- точка на этой прямой
ā= (k, ℓ,m)- направляющий вектор
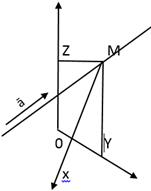 1.Кононическое уравнение прямой(если известен ā =(k, ℓ,m) (ā ML) и M0(X0,Y0,Z0)Є L)
1.Кононическое уравнение прямой(если известен ā =(k, ℓ,m) (ā ML) и M0(X0,Y0,Z0)Є L)
ℓ: 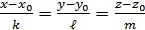

Как линия пересечения плоскостей P1 и P2