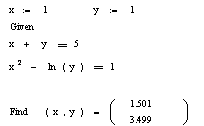Функции для работы с векторами и матрицами

Команды панели инструментов Матрицы
 | создание массива |
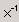 | обратная матрица |
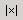 | определитель матрицы |
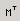 | транспонирование матрицы |
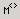 | выделение столбца матрицы |
Нахождение сумм и произведений элементов массивов
Для выполнения вышеуказанных действий используются шаблоны соответствующих команд панели инструментов Calculus:
Рассмотрим параметры команд 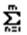 или
или 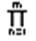
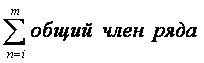
где i – константа, обозначающая номер первого элемента, входящего в сумму ряда;
m – константа, обозначающая номер последнего элемента, входящего в сумму ряда
Рассмотрим параметры команд 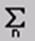 или
или 
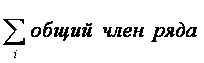
где i – переменная, обозначающая номер элемента ряда.
Например
| Найти сумму всех элементов матрицы В(2х2). | Найти произведение элементов 2-го столбца, той же матрицы. |
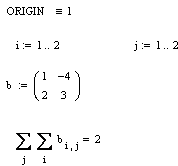 |  |
Уравнения
Численное решение нелинейных уравнений
Для простейших уравнений вида f(x) = 0 или f1(x)=f2(x) решение в Mathcad находится с помощью функции root.
Формат функции: root( f(х), х, a, b )
где,
f(х) - функция, определенная в рабочем документе.
х - имя переменной, аргумент функции. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.
a, b – границы интервала, в пределах которого осуществляется поиск корня. Необязательный параметр. a < b.
Наиболее распространен графический способ определения начальных приближений.
Например . Найти корни уравнения ln(x)=1/x
Порядок выполнения задания:
1. Построим график, для определения приближенного значения корня или интервала, на котором будет находиться предполагаемый корень;
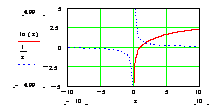
2. Уточним корень, используя функцию root.
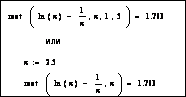
Нахождение корней полинома
Для нахождения корней полинома ,
лучше использовать функцию polyroots(v).
В отличие от функции root, функция polyroots не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные.
Данная функция возвращает корни полинома степени n.
Коэффициенты полинома находятся в векторе v длины n + 1.
Аргументы:
v – вектор, содержащий коэффициенты полинома.
Вектор v удобно создавать использую команду Символы (Symbolics) Коэффициенты полинома (Polynomial Coefficients).
Например. Найти корни уравнения 
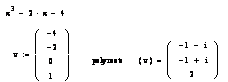
Системы уравнений
Для решения системы уравнений необходимо выполнить следующее:
1. Задать начальное приближение для всех неизвестных, входящих в систему уравнений
2. Напечатать ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений
3. Ввести уравнения и ограничительные неравенства в любом порядке. Используйте [Ctrl]= для печати символа =
4. Введите любое выражение, которое включает функцию Find (Minerr) , например: а:= Find(х, у) или а:= Minerr(х, у).
Например.
5.