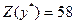Задача на нахождение минимума
Задача № 3.2.
Решить симплексным методом задачу ЛП:
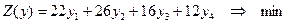 (3.12)
(3.12)
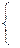
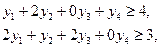 (3.13)
(3.13)
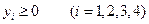 .
.
Решение.
Для решения поставленной задачи симплексным методом от стандартной формы записи задачи ЛП перейдем к канонической. Ведем балансовые переменные 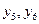
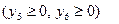 :
:
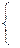
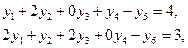 (3.14)
(3.14)
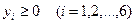 .
.
Составим расширенную матрицу системы (3.14):
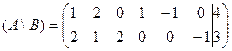
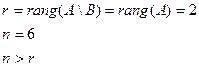
По теореме Кронекера - Капелли система (3.14) совместна и имеет бесчисленное множество решений.
Так как ранг системы (3.14) равен двум, то базисных переменных будет ровно две. Если в качестве базисных переменных, как и в предыдущей задаче, взять балансовые переменные 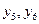 , то первое базисное решение не будет опорным, так как будет содержать отрицательные компоненты. Заметим, что система (3.14) также легко разрешима относительно переменных
, то первое базисное решение не будет опорным, так как будет содержать отрицательные компоненты. Заметим, что система (3.14) также легко разрешима относительно переменных 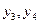 , возьмем их качестве базисных.
, возьмем их качестве базисных.
I. 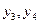 - базисные переменные;
- базисные переменные;
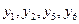 - свободные переменные.
- свободные переменные.
Систему (3.14) решим относительно базисных переменных:
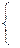
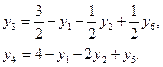 (3.15)
(3.15)
Для контроля выполнимости критерия оптимальности, выразим целевую функцию (3.12) через свободные переменные:
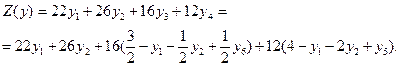
После приведения подобных членов, получим:
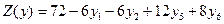 . (3.16)
. (3.16)
В системе (3.15) обнулим свободные переменные, получим первое базисное решение: 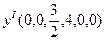 . Все компоненты первого базисного решения решения неотрицательны, следовательно,
. Все компоненты первого базисного решения решения неотрицательны, следовательно, 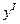 является опорным решением, при котором
является опорным решением, при котором 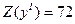 .
.
По виду целевой функции (3.16) на данном шаге легко определить, что решение 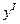 не является оптимальным, т.к. возможно дальнейшее уменьшение целевой функции за счет введения в базис свободных переменных
не является оптимальным, т.к. возможно дальнейшее уменьшение целевой функции за счет введения в базис свободных переменных 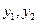 , присутствующих в выражении целевой функции (3.16) с отрицательными коэффициентами. На данном шаге введем в базис переменную
, присутствующих в выражении целевой функции (3.16) с отрицательными коэффициентами. На данном шаге введем в базис переменную 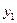 . При этом одну из переменных необходимо вывести из базиса. Предположим, что в системе (3.15) все свободные переменные, кроме
. При этом одну из переменных необходимо вывести из базиса. Предположим, что в системе (3.15) все свободные переменные, кроме 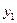 , равны 0. Тогда, для
, равны 0. Тогда, для 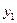 первое уравнение системы (3.15) будет разрешающим, так как увеличить
первое уравнение системы (3.15) будет разрешающим, так как увеличить 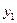 в первом уравнении можно только до 3/2, а во втором до 4 (
в первом уравнении можно только до 3/2, а во втором до 4 ( 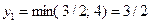 ). Разрешающее уравнение решим относительно
). Разрешающее уравнение решим относительно 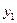 , тем самым введем
, тем самым введем 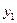 в базис, увеличив до 3/2 ед., а переменную
в базис, увеличив до 3/2 ед., а переменную 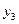 выведем из базиса. Получим
выведем из базиса. Получим 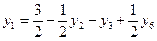 .
.
II . 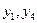 - базисные переменные;
- базисные переменные;
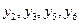 - свободные переменные.
- свободные переменные.
Систему (3.15) перепишем, заменив во втором уравнении 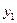 на выражение
на выражение 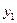 через свободные переменные. Целевую функцию (3.16) также выразим через свободные переменные.
через свободные переменные. Целевую функцию (3.16) также выразим через свободные переменные.
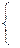
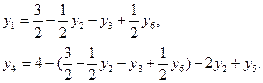
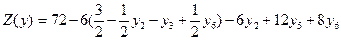 .
.
Приведя подобные члены в системе ограничений и в выражении целевой функции через свободные переменные, получим:
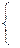
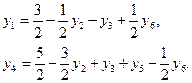 (3.17)
(3.17)
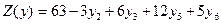 . (3.18)
. (3.18)
Обнулив свободные переменные, получим опорное решение:
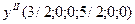 . Значение целевой функции уменьшилось:
. Значение целевой функции уменьшилось: 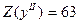 . Но решение
. Но решение 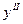 не является оптимальным, так как из (3.18) видно, что возможно дальнейшее уменьшение
не является оптимальным, так как из (3.18) видно, что возможно дальнейшее уменьшение 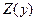 за счет введения свободной переменной
за счет введения свободной переменной 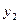 в базис.
в базис.
Увеличить 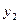 , вводя в базис, можно только до значения
, вводя в базис, можно только до значения 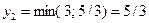 . Следовательно, второе уравнение системы (3.17) на данном шаге является разрешающим. Разрешающее уравнение решим относительно
. Следовательно, второе уравнение системы (3.17) на данном шаге является разрешающим. Разрешающее уравнение решим относительно 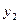 , тем самым введем
, тем самым введем 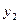 в базис, увеличив до 5/3 ед., при этом одновременно выведем из базиса
в базис, увеличив до 5/3 ед., при этом одновременно выведем из базиса 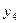 :
: 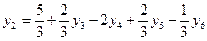 .
.
III. 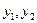 - базисные переменные.
- базисные переменные.
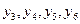 - свободные переменные.
- свободные переменные.
Систему (3.17) перепишем, заменив в каждом из уравнений 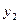 на выражение
на выражение 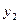 через свободные переменные. Целевую функцию (3.18) также выразим через свободные переменные
через свободные переменные. Целевую функцию (3.18) также выразим через свободные переменные 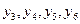 .
.
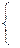
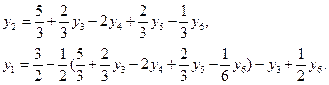
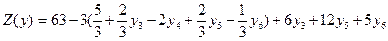 .
.
После приведения подобных членов, получим:
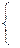
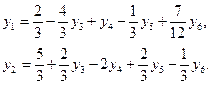 . (3.19)
. (3.19)
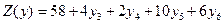 . (3.20)
. (3.20)
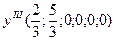 - третье опорное решение.
- третье опорное решение.
Полученное опорное решение будет оптимальным, так как все коэффициенты перед свободными переменными в выражении целевой функции (3.20) положительны и, следовательно, дальнейшее уменьшение целевой функции невозможно.
Ответ. оптимальное решение: 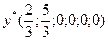 ;
;
значение целевой функции в точке оптимума: