Аналитическое решение поставленной задачи

Порядок расчетов начальных значений приведен в таблице 2, последняя строка которой содержит данные, необходимые для составления системы уравнений (2):

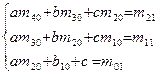, (2)

где m_{40, 30, 20, 10, 21, 11, 01} числа равные соответственно средним значениям x_i⁴, x_i³, x_i², x_i, x_i²y_i, x_iy_i и y_i.

Таблица 2. Начальные значения.

№	xi	yi	xi2	xi3	xi4	xiyi	xi2yi	yi2
		-0,33	1,00	1,00	1,00	-0,33	-0,33	0,11
		1,67	4,00	8,00	16,00	3,34	6,68	2,79
		5,1	9,00	27,00	81,00	15,30	45,90	26,01
		9,6	16,00	64,00	256,00	38,40	153,60	92,16
		15,7	25,00	125,00	625,00	78,50	392,50	246,49
		22,9	36,00	216,00	1296,00	137,40	824,40	524,41
		31,8	49,00	343,00	2401,00	222,60	1558,20	1011,24
Cумма		86,44	140,00	784,00	4676,00	495,21	2980,95	1903,21
Сред.знач.	4,00	12,34857	20,00	112,00	668,00	70,74	425,85	271,89

Подставив все известные значения в систему уравнений (2) получим:

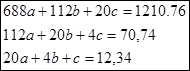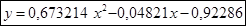Решив данную систему, получаем а=0,673214, b=-0,04821 и с=-0,92286. Тогда уравнение кривой будет иметь вид , что очень похоже на уравнение кривой, когда решали данную задачу графически.

Сравнение фактических y_i и теоретических y_т значений, рассчитанных по уравнению параболы, свидетельствует об удовлетворительном их совпадении (таблица 3).

Расхождение 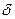между фактическими и теоретическими значениями позволяют найти дисперсию случайных отклонений 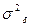по формуле:

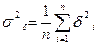, (3)

где 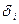вычисляется по формуле:

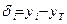(4)

Таблица 3.

№	x	y	yт	сигма	сигма 2
		-0,33	-0,298	-0,03	0,00
		1,67	1,674	0,00	0,00
		5,1	4,991	0,11	0,01
		9,6	9,656	-0,06	0,00
		15,7	15,666	0,03	0,00
		22,9	23,024	-0,12	0,02
		31,8	31,727	0,07	0,01
Сумма		86,44	86,44	0,00	0,04
Сред.знач.	4,000	12,349	12,349	0,000	0,005

Далее вычислим 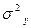дисперсию исходных данных по формуле:

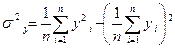, (5)

Из таблицы (3) видно, что 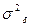= 0,005

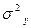= 119,4

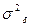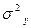Зная значения и можно найти коэффициент корреляции по формуле:

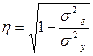, (6)

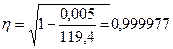
Вывод

Корреляционное отклонение близко к единице, следовательно, параболическая зависимость хорошо аппроксимирует эмпирические данные.

Множественный регрессионный анализ.

Цель работы

По результатам наблюдений x_i и y_i (i = 1, 2 …n) найти оценки неизвестных параметров а₀, а₁ и а_m . Для линейной зависимости модель множественной регрессии записывается в виде:

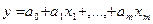, (1)

Исходные данные.

Таблица 1. Исходные данные.

	х1	х2	y
№	Fi, доли ед.	S, доли	Theta, Па
	0,5	0,05
	0,95	0,05
	0,5	0,2
	0,95	0,2
	0,725	0,125
	0,407	0,125
	0,97	0,125
	0,725	0,019
	0,725	0,231
	0,725	0,125

Вычисление переменных.

Процедуру вычисления коэффициентов множественной регрессии рассмотрим на примере регрессии с двумя переменными (факторами):

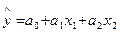, (2)

Таблица 2.

	х1	х2	y	Произведения
№	Fi, доли ед.	S, доли	Theta, Па	x12	x22	y2	x1x1	x1y	x2y
	0,500	0,050		0,25	0,0025		0,0250		0,20
	0,950	0,050		0,90	0,0025		0,0475	11,4	0,60
	0,500	0,200		0,25	0,0400		0,1000		1,20
	0,950	0,200		0,90	0,0400		0,1900	15,2	3,20
	0,725	0,125		0,52	0,0156		0,0900	7,25	1,25
	0,407	0,125		0,16	0,0156		0,0508	1,62	0,50
	0,970	0,125		0,94	0,0156		0,1212	13,58	1,75
	0,725	0,019		0,52	0,0003		0,0137	5,07	0,13
	0,725	0,231		0,52	0,0533		0,1674	9,42	3,00
	0,725	0,125		0,52	0,0156		0,0906	7,25	1,25
СУММЫ	7,177	1,250		5,51	0,2012		0,8971	75,80	13,08
Сред.знач.	0,717	0,125	9,6	0,55	0,0201	108,2	0,0897	7,58	1,30

Найдя суммы полученных произведений можно найти коэффициенты а₁ и а₂ по формулам:

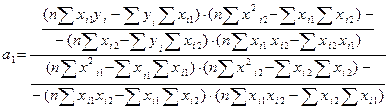, (3)

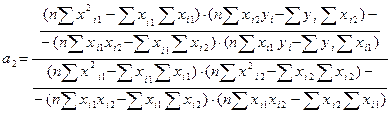. (4)

Подставив известные значения в формулы (3) и (4) получим:

а₁=19,02

а₂=24,14

Зная коэффициенты а₁ и а₂ а также средних значений x_1i , x_2i и y_i найдем значение коэффициента а₀ по формуле:

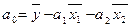, (5)

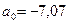
Зная значения коэффициентов а₀, а₁ и а₂ можно найти значений 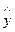по формуле (2). Вычисления 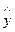представлены в таблице 3.

Таблица 3.

	х1	х2	y
№	Fi, доли ед.	S, доли	Theta, Па	y"
	0,500	0,050		3,6
	0,950	0,050		12,2
	0,500	0,200		7,3
	0,950	0,200		15,8
	0,725	0,125		9,7
	0,407	0,125		3,7
	0,970	0,125		14,4
	0,725	0,019		7,2
	0,725	0,231		12,3
	0,725	0,125		9,7
СУММЫ	7,177	1,250		96,0
Сред.знач.	0,717	0,125	9,6	9,6

Вывод

Мы видим, что полученные значения 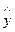очень близки к значениям y, а суммы и средние значения одинаковы. Следовательно, коэффициенты а₀, а₁ и а₂ были найдены правильно. Полученные данные позволяет нам найти зависимость 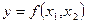, в нашем случае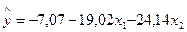

Оценка влияния двух реагентов на предельное напряжение сдвига бурового раствора.

Цель работы: провести полный факторный эксперимент с исходными данными.

Исходные данные

Факторный эксперимент связан с варьированием одновременно всех факторов с проверкой достоверности результатов математико-статистическими методами. В этом разделе производится оценка влияния концентраций двух химических реагентов CaCl₂ и КССБ (концентрированная сульфидспиртовая барда) на величину предельного напряжения сдвига бурового раствора.

Пределы изменения концентраций реагентов:

1. CaCl₂: 0 – 2 %;

2. КССБ: 1 – 3 %.

Проведено четыре эксперимента (N=4) по три параллельных опыта в каждом (n=3).

Исходные данные представлены в табл.1.

Таблица 1

Исходные данные