Описание установки и методика измерений

Применяемый в работе метод по определению σ основан на законе превращения энергии, когда потенциальная энергия растягиваемой из-за действия сил поверхностного натяжения жидкости пружины с подвешенной и находящейся в контакте с жидкостью круглой пластиной, становится сопоставимой с потенциальной энергией (2).

Схема установки изображена на (рис. 3). Подвешенная к пружине круглая пластина находится в контакте с поверхностью исследуемой жидкости. При опускании сосуда с жидкостью из-за действия поверхностного натяжения происходит растягивание пружины, и она приобретает запас потенциальной энергии упругой деформации (к – коэффициент упругости материала пружины.

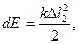(8)

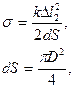(9)

где D – диаметр диска; к – коэффициент упругости материала пружины.

Коэффициент упругости k определяется с помощью подвешенного к пружине эталонного груза m = 100 г.

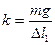(10)

Подставляя (10) и (9) получаем расчетную формулу для определения σ:

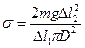(1)1

Порядок выполнения работы

1. Подвесить к пружине эталонный груз и определить растяжение Δl₁. Измерения провести 3 раза.

2. По формуле (10) определить k.

3. Снять эталонный груз, подвесить круглую пластину, взять сосуд с жидкостью и, поднимая его ввести в прикосновение с повешенным диском. Затем, медленно опуская сосуд с пластиной, отметить по шкале значение Δl₂ , при котором пластина оторвется.

4. Измерить 3 раза диаметр диска.

5. Для всех измеренных значений Δl₁, Δl₂, D вычислить средние значения, абсолютную и относительную погрешности. Данные занести в таблицу.

6. Рассчитать σ_ср подставив в формулу (11) значения измеренных величин.

7. На базе формулы (11) получить расчетную формулу для абсолютной погрешности и провести ее расчет (см. обработку результатов). Результаты занести в таблицу, рассчитать относительную ошибку, результат занести в таблицу.

8. Записать окончательный результат по определению σ как

σ_ист=σ_ср±Dσ_ср (12)

Таблица.

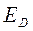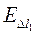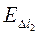N	Δl1		Δl2		D		k	Δk	σ	Δσ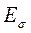
ср. зн.

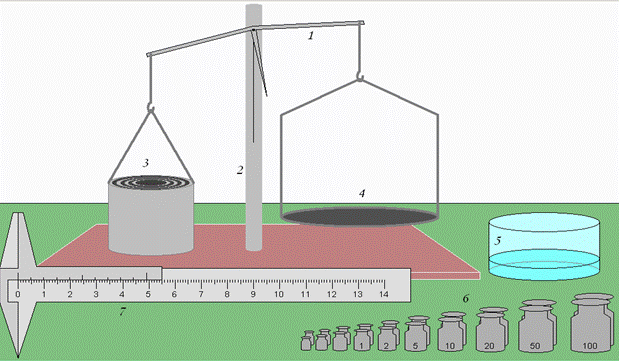
Рис. 6.

Схема экспериментальной установки метода отрыва от ее поверхности

Контрольные вопросы:

1. Чем отличается строение жидкости от кристаллических и газообразных веществ

2. Вывести основную расчетную формулу для определения σ.

3. На чем основан применяемый в данной работе метод. Какие еще методы по определению σ вы знаете.

4. Провести расчет для относительной погрешности .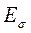

Лабораторная работа № 1-7

Изучение движения тела по наклонной плоскости

Цель работы: изучить равномерное и равноускоренное движение тела по наклонной плоскости при наличии сил трения.

Приборы и принадлежности:

1. Наклонная плоскость с угломером;

2. Линейка;

3. Деревянный брусок;

4. Секундомер.

Краткая теория

Одной из задач данной работы является определение силы трения между двумя поверхностями - плоскости и скользящего по ней тела. Силы трения появляются при перемещении соприкасающихся тел или их частей друг относительно друга. Трение между поверхностями двух твердых тел при отсутствии какой-либо прослойки (например, смазки между ними) называется сухим.Трение между твердым телом и жидкой или газообразной средой называется вязким. Применительно к сухому трению различают трение скольжения и трение качения. В случае сухого трения сила трения возникает не

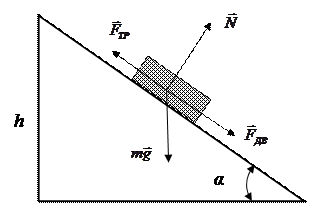
Рис. 1.

Движение тела по наклонной плоскости: (mg – сила тяжести; N – сила реакции опоры; 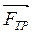- сила трения; 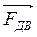- сила движения; h – высота)

только при скольжении одной поверхности по другой, но также и при попытках вызвать такое скольжение. В последнем случае она называется силой трения покоя. Работа сил трения за промежуток времени Δt:

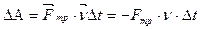(1)

является величиной отрицательной, т.к. векторы F_тр, и v направлены в противоположные стороны. Работа (1) зависит от пути, по которому тело переходит из одного положения в другое. Поэтому сама сила трения, совершающая эту работу, являетсянеконсервативной.

На рис. 1 изображено тело, лежащее на наклонной плоскости. В случае равномерного скольжения по наклонной плоскости:

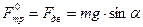(2)

При подъеме незакрепленного конца наклонной плоскости на некоторую высоту h, соответствующую значению угла наклона α₀, компонента F_дв, становится равной силе трения покоя F_тр⁰, и тело, в соответствии с первым законом Ньютона, начинает равномерно скользить вниз по плоскости. Скорость равномерного движения v₀ может быть найдена из энергетического баланса (если пренебречь иными потерями):

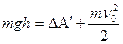(3)

где ΔΑ΄ - работа против сил трения; Δs = l - длина наклонной плоскости.

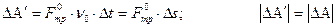(4)

В этом случае коэффициент трения покоя μ₀ определяется как

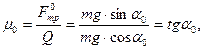(5)

де Q = mg ּ cos 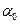- приложена к доске, а не к грузу.

На основе (3) скорость v₀ может быть рассчитана как

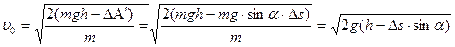(6)

С увеличением h угол наклона растет, и тело будет двигаться с ускорением, т.к. F_дв становится больше силы трения покоя F_тр⁰. Это означает, что сила трения скольжения становится меньше, чем сила трения покоя.

Следовательно, коэффициент трения скольжения будет соответственно также меньше коэффициента трения покоя μ₀ и будет определяться как

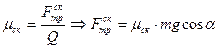(7)

Коэффициенты трения μ_ск и μ₀ в сильной степени зависят от рода и состояния трущихся поверхностей. Кроме того, коэффициент трения скольжения во многих случаях зависит от скорости движения. В начале движения он уменьшается с увеличением скорости, а затем возрастает. В случаях, когда состояние и природа поверхности не изменяются, сила трения скольжения практически не зависит от скорости и равна максимальному значению силы трения покоя. Считается, что в проводимом эксперименте это условие выполняется.