Теорема 2. Признак Даламбера

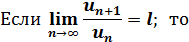
1) при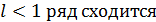

2) при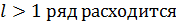

3) при 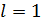вопрос о сходимости остается открытым.

Пример.Исследовать на сходимость ряд:

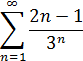
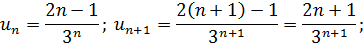
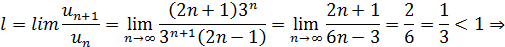
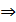по признаку Даламберу ряд сходится.

Теорема 3.Радикальный признак Коши.

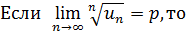
1) при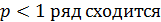

2) при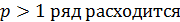

3) при 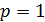вопрос о сходимости остается открытым.

Пример:исследовать на сходимость числовой ряд:

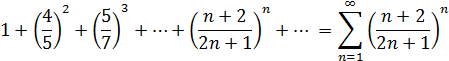
Решение:

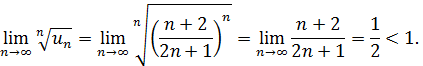
Следовательно, ряд сходится по Коши.

Теорема 4. Интегральный признак Коши.

Пусть члены ряда

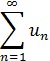
положительны и не возрастают, то есть 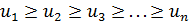и являются значениями непрерывной невозрастающей функции f(x) при x= 1, 2, …, n.

Тогда для сходимости ряда необходимо и достаточно, чтобы сходился несобственный интеграл:

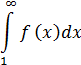
Пример.

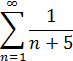
Решение:

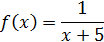
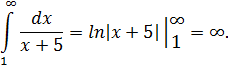
Следовательно, ряд расходится, так как расходится несобственный интеграл.

ЗНАКОПЕРЕМЕННЫЕ РЯДЫ. ПОНЯТИЕ АБСОЛЮТНОЙ И УСЛОВНОЙ СХОДИМОСТИ ЗНАКОПЕРЕМЕНОГО РЯДА.

Ряд называется знакопеременным, если любой его член может быть, как положительным, так и отрицательным.

Рассмотрим знакочередующиеся ряды:

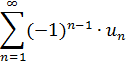
Теорема 1. Признак Лейбница (достаточный признак).

Если у знакочередующегося ряда

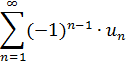
члены убывают по абсолютной величине, то есть 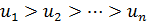и

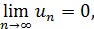
то ряд сходится, и его сумма не превосходит первого члена, то есть S ≤ .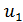

Пример.

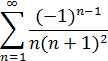
Решение:

Применим признак Лейбница:

.

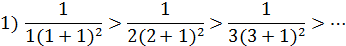
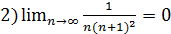Следовательно, ряд сходится по Лейбницу.

Теорема 2. Достаточный признак сходимости знакопеременного ряда.

Если для знакопеременного ряда сходится ряд, составленный из абсолютных величин его членов 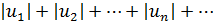, то данный знакопеременный ряд сходится.

Пример: исследовать ряд на сходимость:

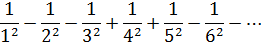
Решение:

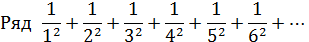
из абсолютных величин членов исходного ряда сходится, как обобщенный гармонический ряд при .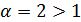

Следовательно, исходный ряд сходится.

Этот признак является достаточным, но не необходимым, то есть существуют знакопеременные ряды, которые сходятся, хотя ряды, составленные из абсолютных величин, расходятся.

Определение 1.Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов.

Определение 2.Знакопеременный ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Отличие между ними в том, что абсолютно сходящийся ряд сходится из-за того, что его члены быстро убывают, а условно сходящийся ряд сходится из-за того, что положительные и отрицательные члены уничтожают друг друга.

Пример.

Решение:

Применим признак Лейбница:

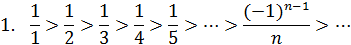
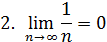
Следовательно, ряд сходится по Лейбницу. Но ряд составленный из абсолютных величин его членов расходится, как гармонический.

Значит, исходный ряд сходится условно.