Описание установки и методика измерений. Установка представляет собой наклонную плоскость с регулируемым и фиксируемым

Установка представляет собой наклонную плоскость с регулируемым и фиксируемым транспортиром углом наклона (рис. 1). Длина плоскости l равномерно разделена на ряд одинаковых отрезков, в конце каждого из ко­торых необходимо определять значения скорости и ускорения соскальзы­вающего бруска при постепенно увеличиваемых углах наклона по из­вестным формулам:

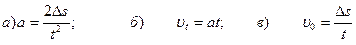(8)

Время прохождения бруском участков Δs фиксируется секундомером. Расчет по формуле (8в) производится при значении угла α₀, когда брусок начинает равномерно скользить по плоскости, случаи (а) и (б) соответствуют углам α > α₀, когда брусок начинает двигаться ускоренно.

Порядок выполнения работы:

1. Взвесить брусок, определить его массу m, записать значение.

2. С помощью транспортира зафиксировать угол α₀, при значении которого брусок начинает скользить равномерно. При этом скорость v₀ определяется по формуле (8в) в конце каждого из отрезков Δs = 25, 50, 75 см с соответствующими значениями времен t₁ = , t₂ = , t₃ = для каждого из этих отрезков. Угол наклона фиксируется нижней поверхностью наклонной плоскости. Измерения провести по 3 раза.

3. Провести расчет коэффициента трения покоя μ₀ по формуле (5).

4. Провести расчет погрешностей (см. обработку результатов).

5. Все результаты занести в табл. 1.

Таблица 1

№ п/п	α0n	Δα0n	εα	ν 025	ν 050	ν 075	μ 0	Δμ0	ε μ
1.
2.
3.
ср. зн.

Увеличивая угол α > α₀ на каждые 5 -7 градусов, добиться равноускоренного движения бруска. Измерения проводить для трех разных углов α, отсчитывая Δs и Δt_n также, как и в п.2. При этом каждый раз фиксиуется высота подъема верхнего конца наклонной плоскости h_n.

6. Для каждого из отрезков Δs_n при данном угле α провести расчет средней скорости и среднего ускорения в конце каждого отрезка по формулам (8а) и (8б). Данные занести в таблицу 2. Средние значения вычисляются на базе 3-х измерений для каждого угла α.

7. Для сравнения на основе баланса энергий по формуле (6) провести расчет скоростей в конце отрезков Δs_n. Результаты занести в таблицу 2.

Сравнивая формулы (1), (3), (7) получить зависимость коэффициента трения скольжения μ_ск от экспериментально найденных значений ско­ростей и провести расчет μ_ск = f(υ_n )для каждого отрезка Δs_n. Результаты расчета занести в таблицу 2 и на основе их построить графики этих зави­симостей для всех углов α_n. Графики построить на миллиметровой бумаге карандашом. При нанесении экспериментальных точек координатные оси необходимо предварительно равномерно разбить на условные единичные отрезки с учетом выбранного масштаба.

Таблица 2

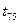t25

t50

v25

v50

v75

α 25

α 50

α 75

h

m

vтеор

μск

α 1

α 2

α 3

3. Провести расчет относительной погрешности и абсолютной погрешности (см. обработку результатов) для каждого угла α_nс использованием соответствующих значений ν_n и s_n.

4. Определить v_теор из уравнения (6).

5. Определить коэффициент трения скольжения из уравнений (3) и (4).

Контрольные вопросы:

1. Дать определение коэффициента трения.

2. Определение коэффициента трения для горизонтальной и наклонной плоскости.

3. Причины возникновения трения.

4. Виды коэффициентов трения.

5. Объяснить полученные графики.

6. Как можно уменьшить силу трения.

7. Определение коэффициентов трения покоя и скольжения.

6. Пояснить баланс энергий формулы (3).

Лабораторная работа № 1 – 8

Изучение закона сохранения энергии на примере маятника Максвелла

Цель работы:изучить закон сохранения энергии

Оборудование:

1. Маятник Максвелла;

2. Линейка;

3. Секундомер;

4. Штангенциркуль.

КРАТКАЯ ТЕОРИЯ

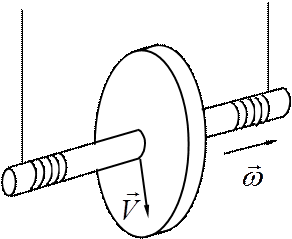
Маятник Максвелла представляет собой маховик с радиусом R на оси радиуса r (см. рис. 1).

	Рис. 1. Схема маятника Максвелла

На эту ось с двух сторон наматываются нити, в результате чего маховик поднимается на высоту h. При освобождении маховик движется вниз и раскручивается под действием момента, создаваемого силами натяжения нитей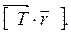

Линейное ускорение 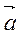, направленное вниз, маятник приобретает под действием разности сил натяжения нитей и силы тяжести. Найдем это ускорение, пренебрегая силами сопротивления. Из следствия из второго закона Ньютона: ma = mg – T; согласно основному уравнению динамики вращательного движения: 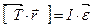(*) . Учитывая, что момент инерции маховика: 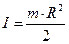( моментом инерции оси можно пренебречь, моментом инерции тела относительно оси называется сумма произведений масс всех материальных точек тела на квадраты их расстояний до оси), и выразив угловое ускорение через линейное: 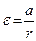, уравнение (*) можно представить в скалярном виде: 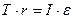, тогда решая полученную систему уравнений: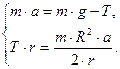

Можно получить: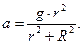

По закону сохранения и превращения энергии (в замкнутой системе энергия может переходить из одних видов в другие и предаваться от одного тела другому, но ее общее количество остается неизменнной), если маятник Максвелла спустится с высоты h, то часть его потенциальной энергии mgh перейдет в кинетическую энергию поступательного движения 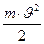и кинетическую энергию вращательного движения 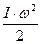, а часть пойдет на совершение работы А против сил сопротивления:

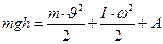(1)

Выразив угловую скорость маховика через линейную получим из (1):

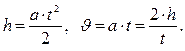(2)

При равноускоренном движении без начальной скорости

Таким образом, измерив время спуска маятника Максвелла, можно найти его линейную скорость в нижней точке υ и, используя (2), определить работу сил сопротивления. Зная А, 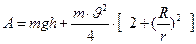можно рассчитать момент сил сопротивления (моментом сил называется 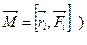по формуле:

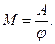(3)