Числовые характеристики непрерывных случайных величин

Ñ Математическим ожиданием непрерывной случайной величины Х с плотностью вероятности j(х) называется величина:

М(Х)= =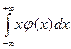

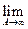
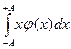
Ñ Дисперсией непрерывной с.в. Х (с математическим ожиданием М(Х)=а и плотностью вероятности j(х)) называется величина:

D(X)=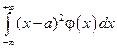

Замечание: Можно доказать, что D(X)= -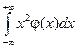

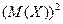
Найдем значения M(X), D(X) в случае примера 7:

M(X)= 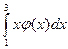= = 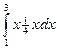= 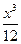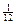(27-1)»2,17.

D(X)= 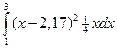= 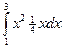- 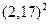= 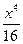- 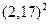» 5,0 – 4,7 = 0,3.

Задачи для самостоятельного решения:

1) Посажено два саженца кустарника разных сортов. Вероятность, что первый приживется 0,8, второй – 0,7. Составить закон распределения для случайной величины, характеризующей возможное количество прижившихся саженцев. Построить многоугольник распределения для соответствующей случайной величины. Найти характеристики: М(Х), s.

2) Одновременно бросают две игральные кости. Составить закон распределения для случайной величины, характеризующей возможную сумму очков на обеих костях. Построить многоугольник распределения для соответствующей дискретной случайной величины. Найти ее характеристики: М(Х), s.

3) Непрерывная случайная величина задана интегральной функцией распределения:

F(X)= 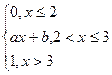(a, b – const.)

Определить: А) Неизвестные параметры: а, b,

Б) Соответствующую функцию плотности распределения,

В) Характеристики: М(Х), s.

4) Непрерывная случайная величина задана плотностью распределения вероятностей:

j(Х)=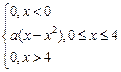

Определить: А) Неизвестный параметр а,

Б) Вероятность попадания случайной величины Х на отрезок [-1,3],

В) Интегральную функцию распределения F(X),

Г) Характеристики: М(Х), s.

Контрольные вопросы

1. Что называется случайной величиной? Привести примеры.
2. Какие случайные величины называются дискретными, а какие непрерывными? Привести примеры дискретных и непрерывных случайных величин.
3. Что представляет собой закон распределения дискретной случайной величины?
4. Как строится многоугольник распределения дискретной случайной величины?
5. Числовые характеристики дискретных случайных величин: математическое ожидание, дисперсия. Что они характеризуют?
6. Как задается интегральная функция распределения непрерывной случайной величины? Ее свойства?
7. Как определяется дифференциальная функция распределения непрерывной случайной величины? Ее свойства?
8. Числовые характеристики непрерывной случайной величины: математическое ожидание, дисперсия

10.4 Некоторые законы распределения
случайных величин
(биномиальный, равномерный, нормальный)

1. Биномиальное распределение

Речь пойдет о серии из n независимых повторных испытаний, в каждом из которых некоторое событие А происходит с одной и той же вероятностью Р(А) = р (вероятность противоположного события 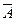, p( 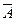) =1- р = q).

Вопрос: Какова вероятность, что событие А при этом произойдет ровно m раз? (m£n).

Пример 1. Монета подбрасывается три раза. Какова вероятность, что «орел» при этом выпадет ровно 2 раза?

Обозначим: А={выпадение «орла» при однократном испытании}.

Очевидно p(А)=0,5; p( 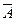)=1- p(А) = 1- 0,5 = 0,5, где

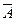={выпадение «решки» при однократном подбрасывании}.

Если исследуемое событие обозначим:

C={При 3-кратном подбрасывании «орел» выпадает 2 раза},

То С 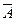= АА 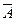+ А А + 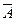АА, то есть «решка» выпадает третий или второй или первый раз. Используя теоремы сложения и умножения вероятностей:

Р(С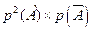) = 3´ 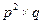=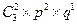3´ = =3 ´ = .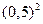

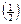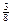В общем случае ответ на поставленный выше вопрос дает Формула Бернулли:

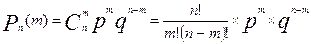
где 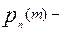вероятность появления события А m раз в серии n повторных испытаний. В общем случае формула доказывается с помощью метода математической индукции.

Пример 2. Вероятность, что саженец яблони приживется, равна 0,8 (из 100 посаженных саженцев, в среднем, 80 приживаются). Какова вероятность, что из 5 посаженных саженцев приживутся:

А) Ровно 3?

Б) Не менее 3?

Решение:

А) Здесь n =5, m=3, p=0,8, q=1- p=0,2.

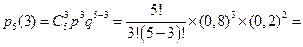10´0,512´0,04=0,2048

Б) Не менее 3, это : или 3, или 4, или 5. Тогда:

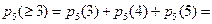0,2048+0,4089+0,3277»0,94.

Так как:

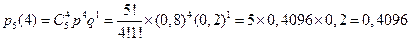
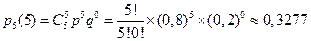
Пример 3. В примере 1 рассчитать вероятности всех возможных исходов, т.е. каковы вероятности, что при трех подбрасываниях монеты «орел» выпадет: ни разу, один, два или три раза?

Решение: n=3, m=0,1,2,3; p=0,5; q=1- p=0,5.

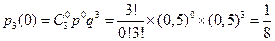; (0!=1)

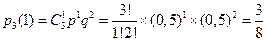
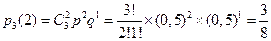
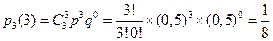
Суммарный подсчет дает:

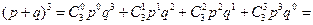
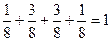
Такое разложение по всем возможным исходам представляет собой биномиальное распределение для случая n=3. Сумма вероятностей всех возможных исходов равна 1, так как они образуют полную группу исходов испытания, кроме того p+q=P(А)+P( 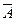)=1.

Замечание: Слово бином дословно переводится как двучлен (некоторая степень суммы двух слагаемых).

В общем случае рассмотрим n независимых испытаний, в каждом из которых событие А происходит с постоянной вероятностью Р(А) = p.

Можно рассмотреть дискретную случайную величину Х, возможные исходы которой – это общее возможное количество наступлений события А, то есть числа: 0, 1, 2, …n-1, n.

В соответствии с формулой Бернулли:

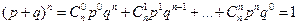
Или располагая полученные значения в таблицу:

x				…	n
				…

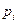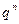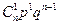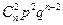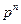Получаем Биномиальный закон распределения для дискретной случайной величины Х.

Числовые характеристики для такой случайной величины:

M(X)=n´p; s =ÖD(X) = Ö(n´p´q).