Теоремы сложения вероятностей. Теоремы умножения вероятностей

Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р(А+В)=Р(А)+Р(В)

Доказательство. Введем обозначения: n—общее

число возможных элементарных исходов испытания; m₁ —

число исходов, благоприятствующих событию А; m₂ —

число исходов, благоприятствующих событию В.

Число элементарных исходов, благоприятствующих

наступлению либо события А, либо события В, равно

m₁ + m₂. Следовательно,

Р (А + В) = (m₁ + m₂)/n — m₁/n + m₂/n.

Приняв во внимание, что m₁/n = P(A) и m₂/n — P{B), окончательно получим

Р(А+В)=Р(А)+Р(В)

Следствие 1. Сумма вероятностей событий А_1, А₂, ..., А_n, образующих полную группу, равна единице: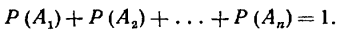

Противоположными называют два единственно

возможных события, образующих полную группу.

Следствие 2. Вероятность противоположных собы-

тий равна 1: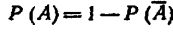

Теорема сложения вероятностей м. б. обобщена на люб. конечное число слагаемых.

Р(А+В+С)=Р(а)+Р(В)+Р(С)-Р(А*В)-Р(А*С)-Р(В*С)+Р(А*В*С)

Вер-ть 2-ух событий равна сумме вер=тей этих событий без вер-ти их совместного наступления

Р(А+В)=Р(А)+Р(В)-Р(А*В)

Условной вероятностью РА (В) называют вероятность

события В, вычисленную в предположении, что событие А

уже наступило.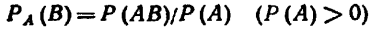

Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

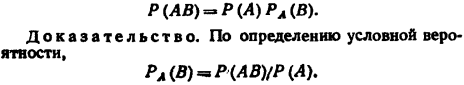
Следствие. Вер-ть совм. появления неск. соб-ий независимых в сов-ти=произвед. вер-ти этих соб-ий Р(А₁, А₂…А_n)=Р(А₁)*Р(А₂)*…Р(А_n)

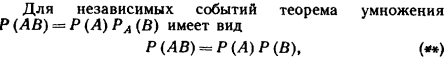
5. Ф-ла полной вер-ти.

Вер-ть гипотез. Ф-ла Байеса.

Повторение испытаний.Ф-ла Бернулли. Наивер-шее число появлений события

Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.

Пусть проводятся п независимых испытаний, в результате которых может появиться событие А с вероятностью р и не поя­виться с вероятностью q, р + q = 1. Появление события А называ­ется успехом, а непоявление — неуспехом. Такая схема называ­ется последовательностью испытаний Бернулли или схе­мой Бернулли.

Пусть X— число успехов в n испытаниях Бернулли. Тогда ве­роятность события {Х= т) (ровно т успехов в п испытаниях) вы­числяется по формуле Бернулли:

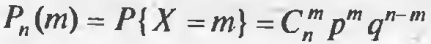
где q-веть того, что соб. А не наступит (q=1-Р(А)=1-р).

Число успехов, кот. при зад. m соот-ет наиб. биномин. вер-ть, наз. наивер-шим числом успехов.

Наивер-шее число успехов чаще 1 число, реже 2, 3 никогда не бывает.