В этом случае интегральная ф-ла Лапласа

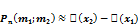
В случае, когда число испытаний велико, формулу Бернулли применять неудобно. Для больших 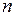существуют приближенные формулы. Точность этих формул увеличивается с возрастанием .

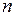Теорема Пуассона:Предположим, что произведение np = 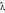является постоянной величиной, когда n неограниченно возрастает, тогда для любого фиксированного m и постоянного

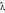
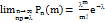На практике эта теорема применяется следующим образом. Если n велико, а p мал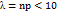о, , то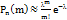

Теорема Пуассона с оценкой погрешности: Пусть 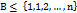произвольное множество целых неотрицательных чисел от 0 до n, 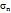– число успехов n испытаний схемы Бернулли, тогда

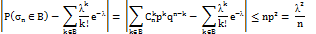
Замечание: Если мало значение q₁ то по Пуассоновским приближениям можно воспользоваться для числа неудач.

Если же n достаточно велико, а p не слишком близко к нулю или единице, то имеет место теорема: Локальная теорема Муавра-Лапласа: 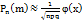, где ,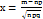

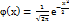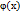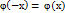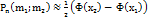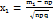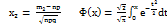а Функция называется ф-ей Гауса. Эта функция затабулирована – ф-ия Гауса чётная. При достаточно больших n вероятность того, что событие A в схеме Бернулли наступило не менее m₁ и не более m₂ раз в n испытаниях, при условии, что p не слишком близко к 0 или 1, вычисляется с помощью след. теоремы: Интегральная теорема Муавра-Лапласа: где , Ф-ия 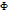(x) называется ф-ией Лапласа, она также затабулирована, она нечётная, т.е. Ф(-x) = Ф(x)

Замечание: Иногда в литературе под ф-ей Лапласа подразумевается др. ф-ия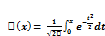

В этом случае интегральная ф-ла Лапласа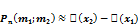

15. Понятие случайной величины(СВ) и ее закона распределения. Функция распределения случайной величины и ее свойства. График функции распределения случайной величины.. Случайной величиной наз-ся переменная величина, к-рая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений.Случайная величина обычно обозначается прописной латинской буквой ( 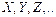), ее конкретные значения – строчными буквами ( 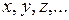).СВ делятся на дискретные и непрерывные, выделяют также смешанные 1) Величина наз-ся дискретной, если она м. принимать определенные, фиксированные значения. 2) СВ вназывается непрерывной, если она может принимать значения, сколь угодно мало отличающиеся друг от друга.Законом распределения СВ называется совокупность пар чисел ( 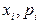), где 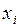– возможные значения случайной величины, а 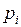– вероятности, с которыми она принимает эти значения, причем 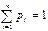.закон. Как для дискретной величины, так и для непрерывной вводится понятие функции распределения. Функция

F(x) = Р(Х < х), х ? (-∞, ∞) называется функцией распределения слу­чайной величины Х Для дискретной случайной величины Х функция распределения имеет вид F(x)=∑p_i

16. Как для дискретной величины, так и для непрерывной вводится понятие функции распределения.

Рассмотрим функцию распределения 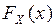случайной дискретной величины , принимающей значения .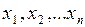

· Если , то 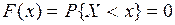, так как в этом случае событие 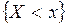является невозможным.

· Если 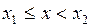, то событие 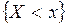наступит тогда и только тогда, когда наступит событие 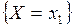, поэтому .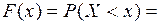

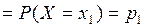· Если 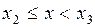, то событие 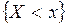равно сумме событи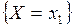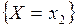й , и .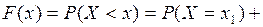

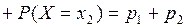· Аналогично, если 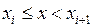, то .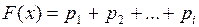

Свойства функции распределения:

1) Функция распределения принимает значения из промежутка : .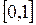

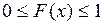2) Вероятность того, что случайная величина примет значение из полуинтервала 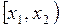, равна разности : .

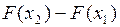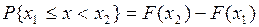3) Функция распределения – неубывающая функция, т.е. 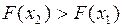при .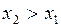

4) .

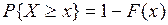5) Если 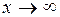, то .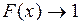

6) Если 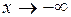, то .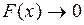

17. Величина называется дискретной, если она может принимать определенные, фиксированные значения.(она принимает конечное либо счетное множество значений)

Случайная величина называется непрерывной, если она может принимать значения, сколь угодно мало отличающиеся друг от друга.

Пусть дискретная случайная величина может принимать 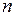значений: 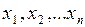. Для полной характеристики этой случайной величины должны быть заданы еще и вероятности появления указанных значений .

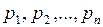18. Наиболее часто используемые законы распределения случайных величин для дискретных случайных величин – это:

· распределение Бернулли (биномиальное распределение);

· распределение Пуассона;

Биномиальное распределение (закон распределения Бернулли) описывает повторяющиеся независимые опыты. Этот закон определяет появление события 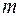раз при 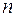независимых испытаниях, если вероятность появления события в каждом из этих 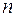опытов 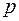не изменяется от опыта к опыту. Вероятность:

,

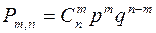где: 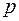– известная вероятность появления события в опыте, не изменяющаяся от опыта к опыту;

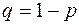– вероятность непоявления события в опыте;

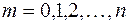– заданное число появления события в 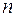опытах;

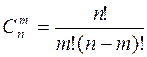– число сочетаний из 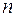элементов по .

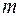Математическое ожидание для биномиального закона распределения 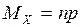, а дисперсия – .

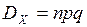Биномиальное распределение широко используется при выборочном методе контроля продукции, т.к. определяет вероятность извлечения из партии продукции заданного количества бракованных изделий при известной доле брака.

Закон Пуассона – предельный случай биномиального распределения, которое превращается в биномиальное распределение, если число опытов бесконечно возрастает, а вероятность 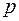появления в каждом из 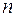опытов стремится к нулю, причем, их произведение 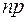стремится к постоянному числу .

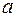Вероятность 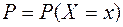того, что случайная величина примет случайное значение 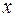, определяется выражением

,

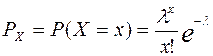где 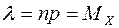– параметр закона Пуассона.

По закону Пуассона распределены:

· число вызовов, поступивших на АТС за единицу времени;

· число некондиционных изделий в выборке при малой вероятности брака и большом объеме партии;

· количество отказов технического устройства в единицу времени;

· количество заявок на обслуживание, поступивших в единицу времени.

19. Наиболее часто используемые законы распределения случайных величин для непрерывных случайных величин – это:

· закон равномерной плотности;

· показательный закон (экспоненциальное распределение);

· нормальный закон распределения.

Закон равномерной плотности используется, если нет оснований считать, что одни значения случайной величины более вероятны, чем другие, во всем диапазоне ( 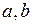) ее возможных значений; поэтому 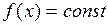в этом диапазоне. Время наступления некоторого события (например, поставки комплектующих) может в первом приближении считаться распределенным равномерно, если известны лишь крайние сроки, но нет никакой информации, уточняющей время наступления данного события.

Математическое ожидание для закона равномерной плотности 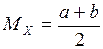, а среднеквадратичное отклонение – .

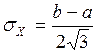Нормальный закон распределения (закон Гаусса) имеет наиболее широкое применение в теории вероятностей и математической статистике. К нормальному распределению близки распределения ошибок измерений, отклонения от номиналов значений характеристик изделий массового изготовления и т.д. Нормальный закон распределения полностью определяется двумя параметрами – математическим ожиданием 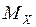и среднеквадратическим отклонением .

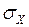Аналитическое выражение нормального закона имеет вид:

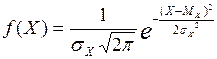
Все значения случайной величины при нормальном распределении лежат с точностью до долей процента в интервале 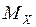±3 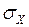, вероятность попадания в который превышает 0,97.

Вероятность попадания нормально распределенной случайной величины в интервал 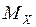±2 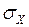составляет более 0,95.

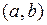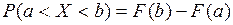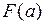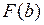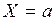Для определения вероятности нормально распределенной случайной величины на участок применяется формула , где и – значения функции распределения случайной величины при и 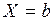, соответственно.

Функция распределения 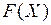нормально распределенной случайной величины имеет вид:

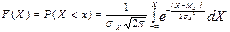
Для вычисления вероятности попадания на заданный участок 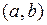используют таблицы интеграла вероятности:

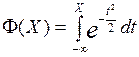
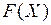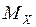Функция распределения нормально распределенной случайной величины с любыми значениями и 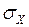связана с 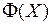выражением:

.

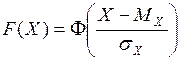Показательный закон (экспоненциальное распределение) выражается формулой 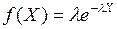, где 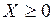, , 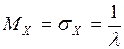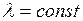. Этот закон принят для распределения случайного времени между двумя событиями, например:

· промежутков между поступлениями двух заявок на обслуживание;

· отказами технического устройства;

· время погрузки или разгрузки;

· время, затраченное на ремонт аппаратуры и т.д.

Математическая статистика основывается на выборочном методе. Множество элементов объекта статистического обследования, обладающих общим свойством, называется генеральной совокупностью, если наблюдению подвергаются все элементы генеральной совокупности, и выборочным, если наблюдению подвергается лишь некоторая доля элементов генеральной совокупности. Количество элементов, составляющих выборку, называется объемом выборки. Выборка имеет ценность, если она правильно отражает основные свойства генеральной совокупности. Статистическую оценку параметров распределения проводят в два этапа. Сначала по выборке получают одно приближенное значение – точечную оценку 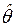некоторого оцениваемого параметра 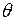, например, оценку 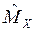математического ожидания 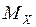, а затем определяют точность и надежность этой оценки.

20 Математическое ожидание дискретной случайной величины и его свойства. Математическое ожидание дискретной случайной величины – это сумма парных произведений всех возможных ее значений на соответствующие вероятности: 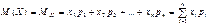, где .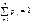

Очевидно, математическое ожидание случайной величины не изменится, если таблицу значений этой случайной величины пополнить конечным числом любых чисел, считая, что вероятности этих чисел равны нулю. Математическое ожидание 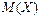случайной величины есть величина постоянная и поэтому представляет числовую характеристику случайной величины .

Свойства математического ожидания: 1) Теорема. Математическое ожидание постоянной величины 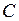равно этой величине. 2) Теорема. Математическое ожидание суммы двух (или нескольких) случайных величин и 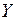равно разности их математических ожиданий:

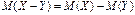.Следствие. Если 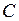– постоянная величина, то: 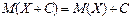3) Теорема. Математическое ожидание произведения двух независимых случайных величин и 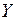равно произведению их математических ожиданий: 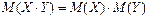. Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин. Действительно, например, для трех взаимно независимых случайных величин , 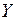и 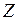: 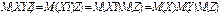, и т.д.

Следствие. Постоянный множитель можно выносить за знак математического ожидания, т.е. .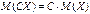

Если 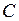– постоянная величина и – любая случайная величина, то, учитывая, что 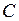и – независимы, получим:

.

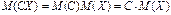Следствие. Математическое ожидание разности двух случайных величин и 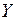равно разности их математических ожиданий: .

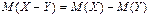Дисперсия дискретной случайной величины и ее свойства. Среднее квадратическое отклонение и моменты дискретной случайной величины.

Теорема. Для любой СВ математическое ожидание ее отклонения равно нулю, т.е.

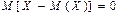.Дисперсией (рассеянием) СВ наз математическое ожидание квадрата отклонения этой величины от ее математического ожидания:

.

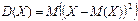Очевидно, что дисперсия СВ постоянна, т.е. явл числовой характеристикой этой величины.

Св-ва дисперсии:

Теорема. Дисперсия постоянной величины равна нулю.

Теорема. Постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат .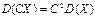

Теорема. Дисперсия СВ = разности математического ожидания ее квадрата и квадрата математического ожидания самой величины: .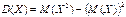

Теорема. Дисперсия суммы двух независимых СВ равна сумме дисперсий этих величин:

.

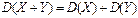Следствие 1. Дисперсия суммы нескольких взаимно независимых СВ = сумме дисперсий этих величин.

Следствие 2. Если 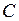– постоянная величина, то .

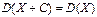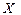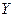Следствие 3. Дисперсия разности двух независимых СВ = сумме дисперсий этих величин, т.е. если СВ и независимы, то .

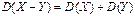Средним квадратичным отклонением 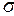(или стандартом) СВ 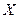называется корень квадратный из дисперсии 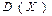этой величины: .

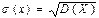21. Правило трех сигм нормально распределенной случайной величины, смысл и значение для практики.

Сущность правила «трех сигм»: Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратичного отклонения.

На практике правило «трех сигм» применяют так: если распределение изучаемой средней величины неизвестно, но правило «трех сигм» выполняется, то есть основания полагать, что изучаемая величина распределена нормально, и наоборот.

22. Математическая статистика основывается на выборочном методе. Множество элементов объекта статистического обследования, обладающих общим свойством, называется генеральной совокупностью, если наблюдению подвергаются все элементы генеральной совокупности, и выборочным, если наблюдению подвергается лишь некоторая доля элементов генеральной совокупности. Количество элементов, составляющих выборку, называется объемом выборки. Выборка имеет ценность, если она правильно отражает основные свойства генеральной совокупности. Статистическую оценку параметров распределения проводят в два этапа. Сначала по выборке получают одно приближенное значение – точечную оценку 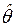некоторого оцениваемого параметра 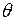, например, оценку 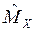математического ожидания 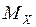, а затем определяют точность и надежность этой оценки.

23.Статистическим распределением выборкиназывают перечень вариант и соответствующих им относительных частот. Статистическое распределение можно представить как:

X			…..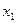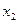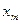
w			….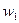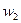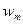

где относительные частоты .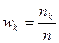

Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – соответствие между наблюдаемыми вариантами и их частотами или относительными частотами.

Приведенный способ представления статистических данных применяют в случае дискретных случайных величин. Для непрерывных случайных величин удобнее разбить отрезок [a,b] возможных значений случайной величины на частичные полуинтервалы 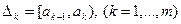( 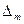замкнут также и справа) с помощью некоторой системы точек 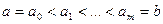. Часто разбиение [a,b] производят на равные части, тогда:

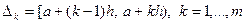
где .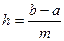

В качестве частот 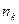теперь надо брать количество наблюдаемых значений, попавших на каждый из частичных интервалов 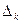. Вариационный ряд имеет в таком случае вид:

X			…..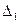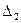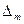
n			….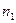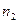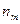

А статистическое распределение –

X			…..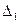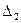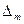
n			….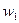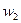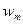

Полигон и гистограмма

Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.

Полигоном частот называют ломаную линию, отрезки которой соединяют точки 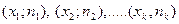. Для построения полигона частот на оси абсцисс откладывают варианты 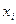, а на оси ординат – соответствующие им частоты 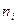и соединяют точки 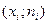отрезками прямых.

Полигон относительных частотстроится аналогично, за исключением того, что на оси ординат откладываются относительные частоты .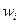

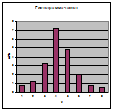
В случае непрерывного признака строится гистограмма, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала 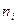– сумму частот вариант, попавших в i–й интервал.

Гистограммой частотназывают ступенчатую фигуру, состоящую из прямоугольников, основаниями которой служат частичные интервалы длиною h, а высоты равны отношению 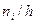. Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии (высоте) 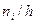. Площадь i–го прямоугольника равна 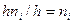– сумме частот вариант i–о интервала, поэтому площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

В случае гистограммы относительных частот по оси ординат откладываются относительные частоты 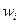, на оси абсцисс – частичные интервалы, над ними проводят отрезки, параллельные оси абсцисс на высоте 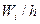. Площадь i–го прямоугольника равна относительной частоте вариант 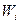, попавших в i–й интервал. Поэтому площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.

24. Статистический и вариационный ряд. Эмпирическая функция распределения и ее свойства. Вариационный ряд для дискретных и непрерывных случайных величин. Пусть из генеральной совокупности извлечена выборка, причем значение исследуемого параметра 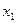наблюдалось 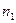раз, 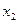- 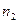раз и т.д. При этом 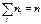объем выборки. Наблюдаемые значения 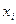называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Числа наблюдений называют частотами, а их отношения к объему выборки 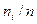- относительными частотами. Вариационный ряд можно представить таблицей вида:

X			..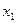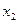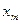
n			.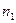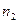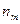

Статистическим распределением выборки называют перечень вариант и соответствующих им относительных частот. Статистическое распределение можно представить как:

X			…..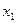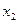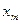
w			….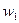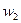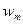

где относительные частоты .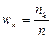

Эмпирической функцией распределения называют функцию 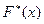, определяющую для каждого значения x относительную частоту события X<x. Таким образом, по определению 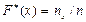, где 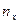– число вариант, меньших x, n – объем выборки.

Свойства эмпирической функции распределения: 1) Значения эмпирической функции принадлежат отрезку [0,1]. 2) 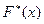– неубывающая функция. 3) Если 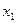– наименьшая варианта, то 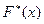=0 при 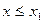, если 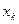– наибольшая варианта, то 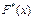=1 при .

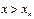Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

25. Математическое ожидание, дисперсия, среднее квадратическое отклонение и моменты непрерывной случайной величины. Мода и медиана непрерывной случайной величины. Неравенство Коши-Буняковского.

Дисперсией непрерывной СВ наз-ся значение интеграла:

.

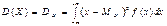Среднее арифмитическое: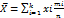

Мода ( 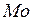) непрерывной СВ – значение, кот соответствует максимальное знач ее плотности вероятности.

Медианой ( 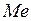) непрерывной СВ - значение, кот опр равенством:

.

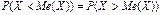Вариационный размах(или широта распр-ния): есть разность между наибольшим и наименьшим значениями выборочного расп-ния: R=xmax-xmin

Начальные и центральные моменты для непрерывных случайных величин находятся по формулам:

,

.

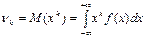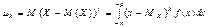Асимметрией распределения случайной величины называется отношение центрального момента третьего порядка к кубу среднего квадратичного отклонения:

.

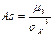Эксцессом распределения случайной величины называют число, определяемое выражением:

.

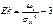Для нормального распределения 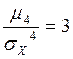, поэтому эксцесс равен нулю.

26. К точечной оценке 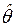предъявляется ряд требований. Она обязательно должна быть:

1. состоятельной (при увеличении объема выборки 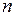значение оценки 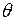должно стремиться (по вероятности) к истинному значению оцениваемого параметра );

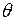2. несмещенной, т.е. чтобы ее математическое ожидание 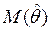было равно оцениваемому параметру ;

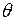3. эффективной, т.е. иметь минимальную дисперсию.

За оценку 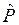вероятности события принимают его частость, за оценку математического ожидания 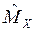– среднее значение 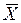полученных реализаций случайной величины .

Для построения интервальной оценки задаются малой вероятностью – уровнем значимости 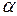(или доверительной вероятностью 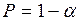) и по полученной точечной оценке и объему выборки находят доверительный интервал.

28. Доверительным интервалом называется такой интервал 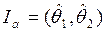значений оценки 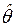, который включает неизвестное истинное значение оцениваемого параметра 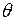с заданной вероятностью 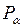, называемой доверительной вероятностью:

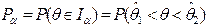
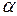– такая малая вероятность выхода истинного значения оцениваемого параметра за пределы интервала 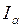, которой можно пренебречь.

Доверительный интервал 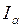характеризует точность оценки параметра, а доверительная вероятность 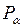– ее надежность: чем больше доверительная вероятность, тем шире доверительный интервал при одном и том же объеме выборки, т.е. выигрывая в надежности оценки, проигрываем в ее точности и наоборот.

Для определения доверительного интервала необходимо знать закон распределения 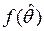оценки .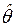