Детерминированные ренты

Если мы хотим оценить серию выплат, которые должны быть сделаны в разные моменты времени, то все эти выплаты должны быть приведены к некоторому фиксированному моменту 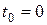, после чего эти выплаты можно складывать, сравнивать и т.д.

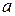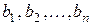С точки зрения приложений к страхованию и пенсионным схемам наиболее важной является задача определения современной стоимости серии из выплат величиной соответственно, которые будут сделаны в некоторые моменты 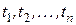в будущем. Величина 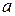может рассматриваться, например, как сумма, которую человек должен внести в пенсионный фонд в момент заключения договора (этот момент обычно принимают за начальный) с тем, чтобы в будущем, в моменты 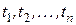, получать пенсию величиной 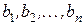. Поэтому

.

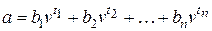Если плата за пенсии производится в виде нескольких платежей величиной 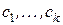, сделанных в моменты 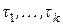, то справедливое соотношение между взносами 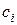и пенсионными выплатами 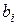находится из принципа эквивалентности обязательств:

.

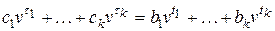Левая часть этой формулы выражает современную ценность всех взносов в пенсионный фонд или страховую компанию, а правая – современную стоимость всех пенсионных выплат.

Описанная таким образом общая модель детерминированной пенсионной схемы на практике обычно не применяется. Реально используются схемы, обладающие той или иной формой регулярности как по величине взносов и выплат, так и по моментам осуществления этих платежей. Особо важным является случай серии платежей фиксированной величины, которые производятся через равные промежутки времени фиксированное число раз. Такие серии платежей обычно называют постоянными рентами илипросто рентами.

Детерминированные постоянные ренты

Рассмотрим последовательных единичных промежутков времени 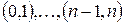. Под моментом 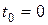обычно будем подразумевать настоящий момент, а в качестве единичного промежутка времени будем рассматривать один год.

Серия из выплат, каждая величиной 1, сделанных в конце этих промежутков, т.е. в моменты 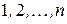, называется запаздывающей рентой.

Серия из выплат, каждая величиной 1, сделанных в начале этих промежутков, т.е. в моменты 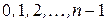, называется упреждающей рентой.

Различие между запаздывающей рентой и упреждающей рентой условное и связано с выбором начала отсчета. Если в качестве начального момента выбрать момент 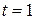, то запаздывающая рента может рассматриваться как упреждающая.

Приведенная стоимость упреждающей ренты в финансовой математике обозначается 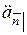. Это – стоимость серии из платежей величиной 1, производимых через единичные интервалы времени. Стоимость этой серии рассчитывается в момент совершения первого платежа. Приведенная стоимость запаздывающей ренты в финансовой математике обозначается .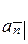

Чтобы вычислить эти величины, нужно привести каждый из платежей к начальному моменту времени 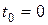, а затем сложить полученные значения:

,

.

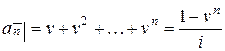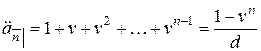Величины 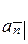и 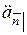позволяют подсчитать величину суммы, которую нужно инвестировать в данный момент для того, чтобы получать фиксированный регулярный доход в будущем. С их помощью также можно определить величину регулярных выплат в случае, когда долг возвращается не одним платежом, а серией одинаковых платежей.

Рассмотренные выше ренты начинались на первом же промежутке 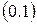(в начале его, т.е. в момент 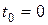, для упреждающей ренты и в конце, т.е. в момент 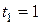, для запаздывающей ренты). Для приложений важны также так называемые отсроченные ренты. Чтобы их определить, рассмотрим последовательные единичные промежутки времени 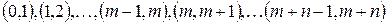( 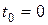– настоящий момент времени).

Серия из выплат, каждая величиной 1, сделанных в конце промежутков 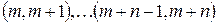, т.е. в моменты 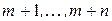, называется запаздывающей отсроченной рентой. Ее стоимость в настоящий момент 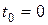обозначается 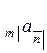. Чтобы подсчитать эту величину, приведем каждый из платежей в моменты 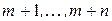к начальному моменту времени, а затем сложим полученные значения:

.

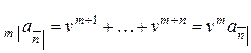Серия из выплат, каждая величиной 1, сделанных в начале промежутков 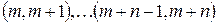, т.е. в моменты 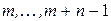, называется отсроченной упреждающей рентой.Ее стоимость в настоящий момент 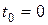обозначается 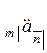. Чтобы подсчитать эту величину, приведем каждый из платежей в моменты 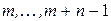к начальному моменту времени, а затем сложим полученные значения:

.

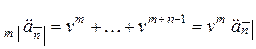Часто полезно знать стоимость ренты не в начальный момент времени, а в конце последнего платежного периода. Эту стоимость можно интерпретировать как общую сумму, накопленную на банковском счете после серии регулярных взносов. Ее обозначают так же, как и соответствующую приведенную стоимость в начальный момент, но с заменой буквы 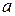на букву .

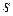Таким образом, 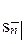– это приведенная стоимость запаздывающей ренты в момент 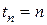последнего платежа, а 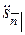– это приведенная стоимость упреждающей ренты в момент 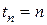, т.е. спустя единицу времени после последнего платежа.

Формулы для накоплени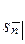й и 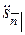можно получить непосредственно, приведя каждый из платежей к моменту 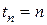и затем складывая полученные значения:

,

.

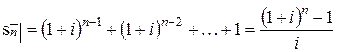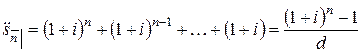Детерминированные постоянные ренты, выплачиваемые с частотой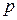

Рассмотрим последовательных промежутков времени 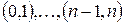. Под моментом 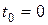как обычно будем подразумевать настоящий момент, а в качестве единичного промежутка будем рассматривать один год.

Разобьем каждый из единичных промежутков на 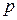равных частей длиной 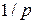каждая.

Серия из 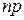выплат, каждая величиной 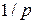, сделанных в конце этих подпромежутков, т.е. в моменты

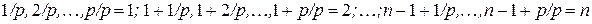
называется запаздывающей рентой, выплачиваемой с частотой 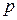. Ее стоимость в настоящий момент времени 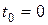обозначается 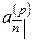, а стоимость в момент 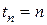последнего платежного периода называется накоплением и обозначается .

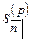Серия из 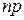выплат, каждая величиной 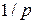, сделанных в начале этих подпромежутков, т.е. в моменты

,

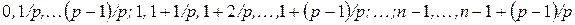называется упреждающей рентой, выплачиваемой с частотой 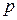. Ее стоимость в настоящий момент времени 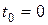обозначается 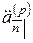, а стоимость в момент 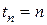последнего платежного периода называется накоплением и обозначается .

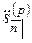Величины 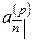и 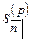, так же как и величины 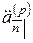и 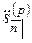, оценивают одну и ту же серию платежей, но в разные моменты времени. Поэтому они связаны соотношениями:

, ,

, ,

.

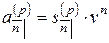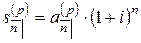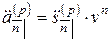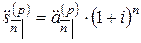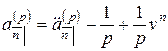Рассмотрим в качестве единичного отрезка времени 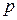-ю долю первоначального единичного отрезка (например, если 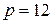и исходный единичный промежуток времени был один год, то новым единичным отрезком времени будет один месяц). Эффективная процентная ставка для этого нового единичного отрезка равна 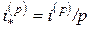, где – номинальная процентная ставка для основного единичного промежутка, начисляемая с частотой 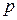. Соответственно, новая учетная ставка равна 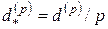, а новое значение коэффициента дисконтирования есть .

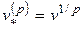Теперь на упреждающую ренту, выплачиваемую с частотой 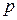на промежутке 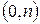, можно смотреть как на обычную упреждающую ренту, выплачиваемую на промежутке 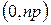. Поскольку каждая выплата равна 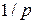, то имеем:

,

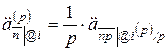где символ 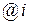указывает эффективную процентную ставку на промежутке, который рассматривается в качестве единичного. Отсюда следует, что:

.

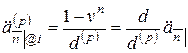Для 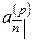верна аналогичная формула:

.

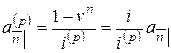Непрерывные ренты

Рассмотрим теперь упреждающую и запаздывающую ренты, которые выплачиваются с частотой 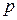на промежутке 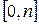, и предположим, что 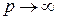. Тогда

,

.

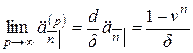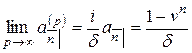Если 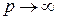, то мы имеем дело с большим числом малых платежей (величиной 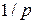каждый), совершаемых через малые промежутки времени 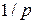. В пределе при 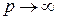можно рассматривать поступление средств как непрерывный процесс, подобный течению жидкости. При этом в пределе различие между платежами в начале и в конце промежутков исчезнет. Непрерывный поток платежей называется непрерывно выплачиваемой рентой. Приведенная стоимость непрерывного потока платежей в момент 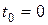обозначается .

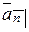Рассматривая поступление средств в предельном случае 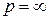как непрерывный поток жидкости, непосредственно определим величину 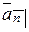как интеграл

.

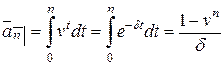Можно ввести и произвольную непрерывную ренту на промежутке 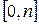, которая характеризуется произвольной скоростью 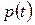поступления средств в момент . Для такой ренты приведенная стоимость в момент 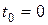равна интегралу

.

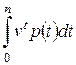Непрерывные ренты часто используются как приближения для рент, которые выплачиваются достаточно часто:

, .

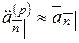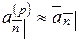Можно получить и более точные формулы:

,

.

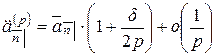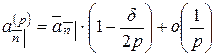Сумма, накопленная к моменту при непрерывном поступлении средств со скоростью 1, обозначается 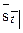. Чтобы ее вычислить, нужно сумму 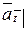привести к моменту :

.

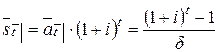Детерминированные возрастающие ренты

Рассмотрим последовательных единичных промежутков времени 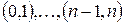. Под моментом 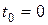как обычно будем подразумевать настоящий момент, а в качестве единичного промежутка времени будем рассматривать один год.

Серия из 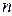выплат величиной 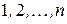, сделанных в конце этих промежутков, т.е. в моменты 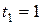, ,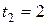…, , 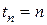называется запаздывающей возрастающей рентой. Ее приведенная стоимость в момент 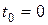в финансовой математике обозначается 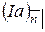. Для подсчета этой величины нужно все платежи привести к начальному моменту, а затем сложить:

.

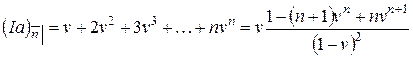Серия из выплат величиной 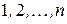, сделанных в начале промежутков 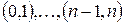, т.е. в моменты 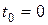, ,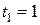…, , 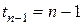называется упреждающей возрастающей рентой. Ее приведенная стоимость в момент 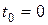в финансовой математике обозначается :

.

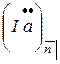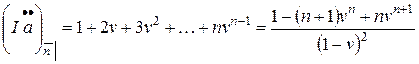Резюме

Методы теории вероятностей используются во многих областях человеческой деятельности. Понятия случайных событий и случайных величин важнейшие в теории вероятностей. Случайные события обозначают заглавными латинскими буквами 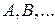и т.д., а случайные величины 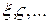и т.д.

При решении задач необходимо уметь составлять законы распределения дискретных и непрерывных случайных величин, а также находить их основные числовые характеристики (математическое ожидание, дисперсия, среднее квадратическое отклонение). В актуарной математике особое значение имеет центральная предельная теорема, которая используется для оценки вероятности разорения страховых компаний.

При актуарных расчетах широко используются методы финансовой математики, например, в долгосрочном страховании применяется теория сложных процентов, а оценивание стоимости страховых рент опирается на оценку стоимости финансовых рент.

Вопросы для самопроверки

1. Понятие случайного события. Действия над случайными событиями.

2. Вероятностное пространство. Аксиоматическое определение вероятности.

3. Случайные величины. Закон распределения.

4. Важнейшие распределения случайных величин (Бернулли, биномиальное, Пуассона, геометрическое, равномерное, нормальное, экспоненциальное).

5. Основные числовые характеристики случайных величин. Их свойства.

6. Центральная предельная теорема и ее следствия.

7. Простые и составные проценты.

8. Интенсивность процентов. Номинальные процентные ставки.

9. Приведенная стоимость.

10. Виды финансовых рент. Их современная стоимость.