Что значит решить систему дифференциальных уравнений?
Это значит, найти такие функции  и
и 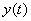 , которые удовлетворяют и первому и второму уравнению системы. Как видите, принцип очень похож на обычныесистемы линейных уравнений. Только там корнями являются числа, а здесь – функции.
, которые удовлетворяют и первому и второму уравнению системы. Как видите, принцип очень похож на обычныесистемы линейных уравнений. Только там корнями являются числа, а здесь – функции.
Найденный ответ записывают в виде общего решения системы дифференциальных уравнений:
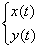
В фигурных скобках! Эти функции находятся «в одной упряжке».
Для системы ДУ можно решить задачу Коши, то есть, найти частное решение системы, удовлетворяющее заданным начальным условиям. Частное решение системы тоже записывают с фигурными скобками.
Более компактно систему можно переписать так:
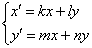
Но в ходу традиционно более распространен вариант решения с производными, расписанными в дифференциалах, поэтому, пожалуйста, сразу привыкайте к следующим обозначениям:
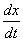 и
и 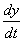 – производные первого порядка;
– производные первого порядка;
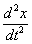 и
и 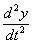 – производные второго порядка.
– производные второго порядка.
Пример 1
Решить задачу Коши для системы дифференциальных уравнений 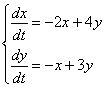 с начальными условиями
с начальными условиями 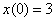 ,
, 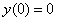 .
.
Решение: В задачах чаще всего система встречается с начальными условиями, поэтому почти все примеры данного урока будут с задачей Коши. Но это не важно, поскольку общее решение по ходу дела все равно придется найти.
Решим систему методом исключения. Напоминаю, что суть метода – свести систему к одному дифференциальному уравнению. А уж дифференциальные уравнения, надеюсь, вы решаете хорошо.
Алгоритм решения стандартен:
1) Берем второе уравнение системы 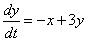 и выражаем из него
и выражаем из него 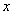 :
:
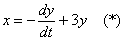
Данное уравнение нам потребуется ближе к концу решения, и я помечу его звёздочкой. В учебниках, бывает, натыкают 500 обозначений, а потом ссылаются: «по формуле (253)…», и ищи эту формулу где-нибудь через 50 страниц сзади. Я же ограничусь одной единственной пометкой (*).
2) Дифференцируем по 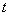 обе части полученного уравнения
обе части полученного уравнения 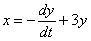 :
:
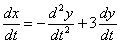
Со «штрихами» процесс выглядит так:
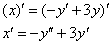
Важно, чтобы этот простой момент был понятен, далее я не буду на нём останавливаться.
3) Подставим 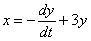 и
и 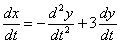 в первое уравнение системы
в первое уравнение системы 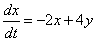 :
:
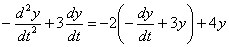
И проведём максимальные упрощения:
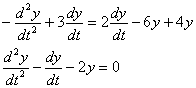
Получено самое что ни на есть обычное однородное уравнение второго порядка с постоянными коэффициентами. Со «штрихами» оно записывается так: 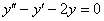 .
.
Составим и решим характеристическое уравнение:
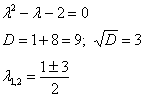
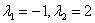 – получены различные действительные корни, поэтому:
– получены различные действительные корни, поэтому:
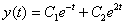 .
.
Одна из функций найдена, пол пути позади.
Да, обратите внимание, что у нас получилось характеристическое уравнение с «хорошим» дискриминантом, а значит, мы ничего не напутали в подстановке и упрощениях.
4) Идём за функцией  . Для этого берём уже найденную функцию
. Для этого берём уже найденную функцию 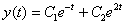 и находим её производную. Дифференцируем по
и находим её производную. Дифференцируем по 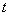 :
:
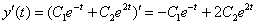
Подставим 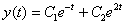 и
и 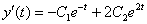 в уравнение (*):
в уравнение (*):
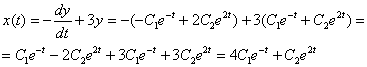
Или короче: 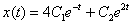
5) Обе функции найдены, запишем общее решение системы:
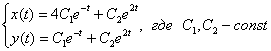
6) Найдем частное решение, соответствующее начальным условиям 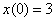 ,
, 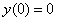 :
:
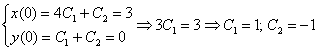
Здесь из первого уравнения я почленно вычел второе уравнение, более подробно о методе можно прочитать в статье Как решить систему линейных уравнений?
Ответ: частное решение: 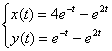
Полученный ответ достаточно легко проверить, проверку осуществим в три шага:
1) Проверяем, действительно ли выполняются начальные условия 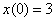 ,
, 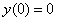 :
:
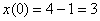
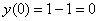
Оба начальных условия выполняются.
2) Проверим, удовлетворяет ли найденный ответ первому уравнению системы 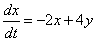 .
.
Берём из ответа функцию 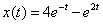 и находим её производную:
и находим её производную:
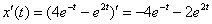
Подставим 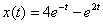 ,
, 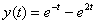 и
и 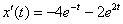 в первое уравнение системы:
в первое уравнение системы:
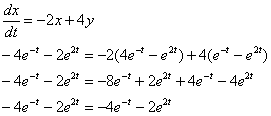
Получено верное равенство, значит, найденный ответ удовлетворяет первому уравнению системы.
3) Проверим, удовлетворяет ли ответ второму уравнению системы 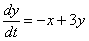
Берём из ответа функцию 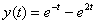 и находим её производную:
и находим её производную:
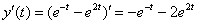
Подставим 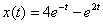 ,
, 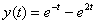 и
и 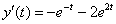 во второе уравнение системы:
во второе уравнение системы:
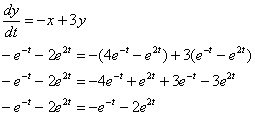
Получено верное равенство, значит, найденный ответ удовлетворяет второму уравнению системы.
Проверка завершена. Что проверено? Проверено выполнение начальных условий. И, самое главное, показан тот факт, что найденное частное решение 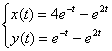 удовлетворяет каждому уравнению исходной системы
удовлетворяет каждому уравнению исходной системы 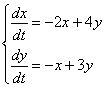 .
.
Аналогично можно проверить и общее решение 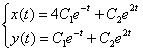 , проверка будет даже еще короче, так как не надо проверять выполнение начальных условий.
, проверка будет даже еще короче, так как не надо проверять выполнение начальных условий.
Теперь вернемся к прорешанной системе и зададимся парой вопросов. Решение начиналось так: мы взяли второе уравнение системы 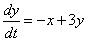 и выразили из него
и выразили из него 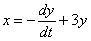 . А можно ли было выразить не «икс», а «игрек»? Если мы выразим
. А можно ли было выразить не «икс», а «игрек»? Если мы выразим 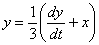 , то это нам ничего не даст – в данном выражении справа есть и «игрек» и «икс», поэтому нам не удастся избавиться от переменной и свести решение системы к решению одного дифференциального уравнения.
, то это нам ничего не даст – в данном выражении справа есть и «игрек» и «икс», поэтому нам не удастся избавиться от переменной и свести решение системы к решению одного дифференциального уравнения.
Вопрос второй. Можно ли было начать решение не со второго, а с первого уравнения системы? Можно. Смотрим на первое уравнение системы: 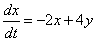 . В нём у нас два «икса» и один «игрек», поэтому необходимо выразить строго «игрек» через «иксы»:
. В нём у нас два «икса» и один «игрек», поэтому необходимо выразить строго «игрек» через «иксы»: 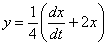 . Далее находится первая производная:
. Далее находится первая производная: 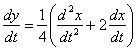 . Потом следует подставить
. Потом следует подставить 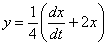 и
и 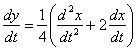 во второе уравнение системы. Решение будет полностью равноценным, с тем отличием, что сначала мы найдем функцию
во второе уравнение системы. Решение будет полностью равноценным, с тем отличием, что сначала мы найдем функцию  , а затем
, а затем 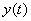 .
.
И как раз на второй способ будет пример для самостоятельного решения:
Пример 2
Найти частное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.
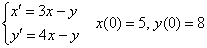
В образце решения, который приведен в конце урока, из первого уравнения выражен 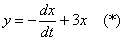 и вся пляска начинается от этого выражения. Попытайтесь самостоятельно по пунктам провести зеркальное решение, не заглядывая в образец.
и вся пляска начинается от этого выражения. Попытайтесь самостоятельно по пунктам провести зеркальное решение, не заглядывая в образец.
Можно пойти и путём Примера №1 – из второго уравнения выразить 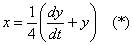 (заметьте, что выразить следует именно «икс»). Но этот способ менее рационален, по той причине, что у нас получилась дробь, что не совсем удобно.
(заметьте, что выразить следует именно «икс»). Но этот способ менее рационален, по той причине, что у нас получилась дробь, что не совсем удобно.
