A)Вывод дифференциального уравнения

Курсовая работа

по дисциплине

“Математические методы в электронике”

Тема: «Моделирование процессов в электрических цепях на основе дифференциальных уравнений»

Выполнил:

Студент 2 курса группы № 2142

Шитенков Михаил Олегович

Руководитель: проф. Трофимов А. Т.

Дубна, 2014

Оглавление

a)Вывод дифференциального уравнения. 4

Моделирование процессов в цепи в среде математического моделирования MathCAD. 5

b) Переходный процесс. Решение неоднородного дифференциального уравнения, описывающего зависимость выходного напряжения от входного сигнала (единичного скачка напряжеиня) цепи. 5

c) Свободные колебания напряжения на катушке. Наблюдение за выходным напряжением цепи при начальном значение выходного напряжения Y(t)=1.( ЕДС не подается, заряд накомлен в катушке индективности) 6

d) Решение дифференциального уравнения , описывающего зависимость выходного напряжения от входного сигнала цепи, с входным сигналом заданным дифференциалом от функции Гаусса. 7

Основные Выводы. 9

Государственное бюджетное образовательное учреждение

высшего профессионального образования Московской области

Международный университет Природы, Общества и Человека «Дубна»

Кафедра Персональной Электроники

ЗАДАНИЕ

на курсовую работу по дисцеплине «Математические методы в электронике»

Тема курсовой работы:

Моделирование процессов в электрических цепях на основе дифференциальных уравнений.

Задачи, решаемые в работе:

1)Наша задача заключается в моделирование процесса, происходящего в радиотехнической цепи, при подаче на него определенного сигнала, на примере решения дифференциального уравнения. Нам дана схема электрическая принципиальная. Необходимо написать программу для решения дифференциальных уравнений в среде MathCAD.

a) Составить дифференциальное уравнение, описывающее процесс изменения выходного напряжения на катушке индуктивности в заданной радиотехнической цепи.

b) Наити решение неоднородного дифференциального уравнения описывающего зависимость выходного напряжения от входного сигнала цепи при условии, что выходное напряжение в момент времени t=0 тоже равно 0 ( Y(t)=0). И мы подаем на цепь в момент времени равный 0 единичный скачек напряжения.

c) Наити решение однородного дифференциального уравнения, описывающего зависимость выходного напряжения цепи от времени, при условии, что выходное напряжение в момент времени t=0 равно 1 ( Y(t)=1). Пронаблюдать свободные колебания в цепи.

d) Наити решение неоднородного дифференциального уравнения, описывающего зависимость выходного напряжения от входного сигнала цепи, при условии, что выходное напряжение в момент времени t=0 тоже равно 0( Y(t)=0, Y`(t)=0). И при условии, что входной сигнал имеет вид производной от функции Гаусса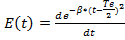

2) Привести графики выходных сигналов и сделать выводы о прохождении сигнала через соответствующую цепь.

Исходные данные:

Входной сигнал имеет форму:

1) Функция Хевисайда ( Единичного скачка),

2) Производная от функции Гаусса с параметрами: длительность Те = 2.

Отношение индуктивность/сопротивление: τ = 0.2*Те α = 1/τ => α = 2.5

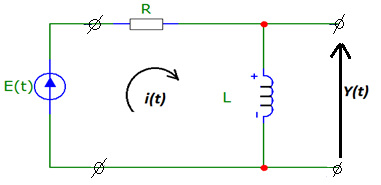Схема цепи имеют следующий вид:

Дата выдачи задания 25.04.2014

Дата защиты___________

Студент гр. 2142

Преподаватель Трофимов А.Т. ____

a)Вывод дифференциального уравнения.

Процессы в цепи описываются дифференциальным уравнением 1 порядка, составленным по второму закону Кирхгофа:

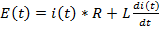…………..…………………….(1.1)

Для RL – цепи.

Обозначим выходное напряжение как Y(t). 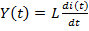…………….…………….(1.2)

Выразим из формулы i(t) . 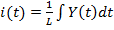…………………..……………………(1.3)

Подставим ток, выраженный через выходное напряжение в уравнение Кирхгофа.

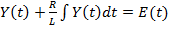…………….……………………..(1.4)

Продифференцируем предыдущее уравнение.

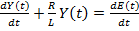…………………………………………(1.5)

Это и является дифференциальным уравнением, описывающим изменение выходного напряжения от входного напряжения в RL цепи.

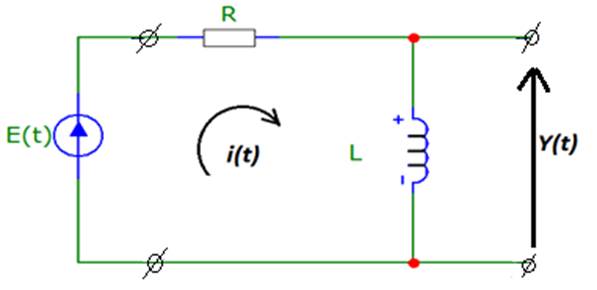
Рисунок 1. Принципиальная схема электрической цепи.