Приближенное вычисление
На практике часто встречаются интегралы, которые не выражаются через элементарные функции. В этом случае интегралы можно взять приближенными методами: по формулам прямоугольников, трапеций и Симпсона.
По формуле трапеций интеграл вычисляется как
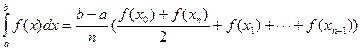 ,
,
где 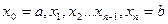 - точки отрезка [a; b].
- точки отрезка [a; b].
Предельная погрешность формулы трапеций составляет 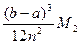 , где M2– наибольшее значение |f²(x)| в промежутке [a; b].
, где M2– наибольшее значение |f²(x)| в промежутке [a; b].
Пример. 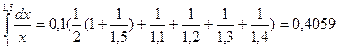 .
.
По формуле Симпсона (параболических трапеций) интеграл вычисляется как
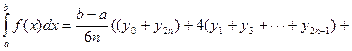
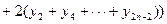
Предельная погрешность формулы Симпсона составляет 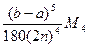 , где M4– наибольшее значение |fIV(x)| в промежутке [a; b].
, где M4– наибольшее значение |fIV(x)| в промежутке [a; b].
Применение определенного интеграла
Площадь плоской фигуры, ограниченной функциями y1 и y2
Площадь плоской фигуры S, ограниченной функциями y1 и y2, определяется по формуле (рис.5.1)


 Х
Х 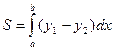 . (1)
. (1)
y2

 y1
y1
 |
0 а в у
Рис. 5.1. Площадь плоской фигуры S,
ограниченной функциями y1 и y2
@ Задача 1. Найти площадь криволинейного треугольника, ограниченного функцией y = x2, осью OX и x = 1.
Решение: В формуле (1) вместо y1 ставится функция y = x2, вместо y2 функция y = 0 (ось OX), вместо a значение x пересечения y1 и y2, т.е. a = 0, b = 1 (x = 1):
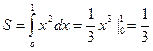 .
.
@ Задача 2. Найти площадь фигуры, ограниченной функциями y1 = x и y2 = x3.
Решение: В формуле (1) a и b являются точками пересечения функций y1 и y2, т.е. a = 0 и b = 1:
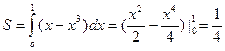 .
.
Объем тел вращения
Объем V пространственного тела, полученного вращением графика функции f(x) вокруг оси OX, определяется по формуле 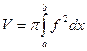 .
.
@ Задача 3. Найти объем эллипсоида вращения:
Решение: Объем эллипсоида вращения определяется как
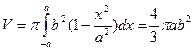 .
.
Применение определенного интеграла в экономике
С помощью определенного интеграла можно найти доходы, издержки, объем продукции (выпуск) и т.д., интегрируя предельные доходы, издержки и производственную функцию.
@ Задача 4.Найти суммарный доход R(Q), зная предельный доход 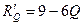 .
.
Решение: Суммарный доход находится как интеграл от предельного дохода
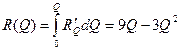 .
.
Неопределенный множитель C = 0, т.к. R(0) = 0.
@ Задача 5.Найти объем продукции производства за 4 года, если производственная функция имеет вид 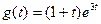 .
.
Решение: Объем продукции Q определяется как
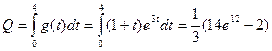 .
.
Кривая Лоренца
Кривая Лоренца показывает распределение доходов в обществе, т.е. зависимость суммарного дохода от численности населения. Если бы распределение доходов было равномерным, то график функции шел бы по диагонали квадрата со стороной 1. Чем больше отклонение кривой Лоренца от диагонали квадрата, тем больше степень неравномерности распределения доходов в обществе. Отношение площади полученной криволинейной фигуры к площади треугольника ACD (рис. 5.2) называется «коэффициентом Джини». Этот коэффициент можно найти по формуле
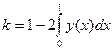 ,
,
где y(x) – кривая Лоренца.
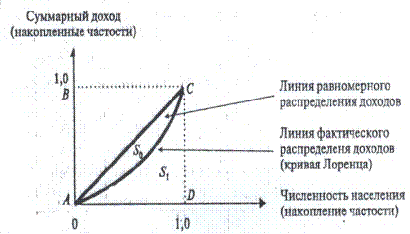
Рис. 5.2. Кривая Лоренца
