Неопределенный интеграл

Первообразная функция и неопределённый интеграл. Свойства неопределённого интеграла. Интегралы от основных элементарных функций. Метод замены переменной. Метод интегрирования по частям. Интегрирование простейших рациональных дробей. Интегрирование тригонометрических функций. Интегрирование некоторых иррациональных функций.

Определенный интеграл

Понятие определённого интеграла, его геометрический и экономический смысл. Свойства определённого интеграла. Определённый интеграл как функция верхнего предела. Формула Ньютона – Лейбница. Замена переменной и формула интегрирования по частям в определённом интеграле. Геометрические приложения определённого интеграла. Использование понятия определённого интеграла в экономике. Непосредственное вычисление определенного интеграла

и подведение под знак дифференциала. Несобственные интегралы. Кратные интегралы.

Дифференциальные уравнения

Основные понятия и определения. Дифференциальные уравнения первого порядка. Уравнения n-го порядка, допускающие понижение порядка. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами.

Ряды

Понятие ряда и его сходимости. Свойства сходящихся рядов. Признаки сходимости положительных рядов. Знакопеременные ряды. Абсолютная и условная сходимость. Функциональные ряды. Степенные ряды. Ряды Тейлора и Маклорена. Применение рядов к приближенным вычислениям.

Контрольная работа № 1

Раздел I

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

1.1. Дан параллелограмм ABCD, три вершины которого заданы (табл. 1.1). Найти четвертую вершину и острый угол параллелограмма.

1.2. Найти длину высоты AD в треугольнике с вершинами А, В, С (табл. 1.2) и написать уравнение перпендикуляра, опущенного из точки С на прямую АВ.

1.3. Найти угол между плоскостью 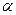и прямой, проходящей через начало координат и точку М (табл. 1.3). Вычислить расстояние от точки М до плоскости .

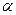1.4. Написать уравнения перпендикуляра, опущенного из точки М на прямую J (табл. 1.4).

1.5. Построить кривые по заданным уравнениям (табл. 1.5).

Таблица 1.1

Варианты задания 1.1

Вариант	А	В	С	Вариант	А	В	С
	(–1; –2; 3)	(–4; 1; 2)	(5; 2; 7)		(–3; 5; –4)	(–5; 6; 2)	(3; –5; –2)
	(1; 2; 3)	(3; –4; –2)	(–4; –3; 2)		(2; –3; 4)	(6; –4; –5)	(–3; 4; –2)
	(2;–3; –1)	(–3; 5; 3)	(4; 3;–4)		(5; –2; –4)	(–5; –8; –1)	(–2; 4; 3)
	(3; –4; 2)	(–5; 2; –3)	(–1; 7; –2)		(–3; –2; –5)	(–4; –5; 3)	(2; 3; 4)
	(–5; 2; 4)	(–3; –4; 2)	(6; –3; –3)		(2; 6; –3)	(–5; –2; –4)	(–3; –5; 1)

Таблица 1.2

Варианты задания 1.2

Вариант	А	В	С	Вариант	А	В	С
	(3; 4)	(2; –1)	(1; –7)		(3; 2)	(2; –5)	(–6; –1)
	(–4; –5)	(3; 3)	(5; –2)		(6; –4)	(–3; –7)	(–1; 2)
	(–3; 5)	(4; –3)	(–2; –4)		(–2; –1)	(7; 3)	(4; –3)
	(3; –2)	(–5; –4)	(–1; 6)		(3; 4)	(6; 7)	(1; 1)
	(2; 5)	(–3; 4)	(–4; –2)		(–4; –5)	(–2; 2)	(–7; 4)

Таблица 1.3

Варианты задания 1.3

Вариант	M		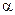Вариант	M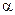
	(2; –1; 3)	3x – y + 2z – 4 = 0		(–2; 4; –3)	x + 5y + 7z –2 = 0
	(2; –2; 4)	x – 3y + 5z – 10 = 0		(5; –3; 2)	–x + 3y + 2z + 14 = 0
	(–4; 5; –1)	4x + y – 2z + 5 = 0		(–3; –5; –4)	–3x + 2y + z – 4 = 0
	(–3; 2; 1)	2x – y + z + 5 = 0		(–3; –2; 4)	x –5y + 3z + 1 = 0
	(2; 3; 1)	5x + 2y – z – 3 = 0		(1; 3; 4)	2x + 3y + z – 6 = 0

Таблица 1.4

Варианты задания 1.4

Вариант	M	J	Вариант	M	J
	(3; 2; 1)		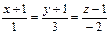	(–4; 5; –2)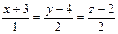
	(2; –1; 3)		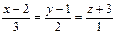	(5; –2; 3)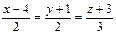
	(1; –3; 2)		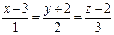	(–1; –3; –2)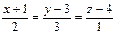
	(–4; 2; –3)		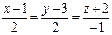	(2; –5; –4)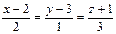
	(–4; 5; 2)		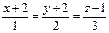	(4; 3; –5)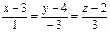

Таблица 1.5

Варианты задания 1.5

Вариант	Уравнения	Вариант	Уравнения

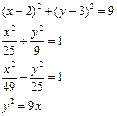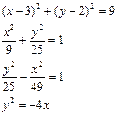Окончание табл. 1.5