Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами

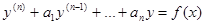где а₁,…,a_n = const. Его решения могут быть найдены в два этапа:

Первый этап. Находят общее решение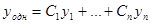

Второй этап. Находят частное решение y^* методом вариации произвольных постоянных, т.е. общее решение неоднородного дифференциального уравнения

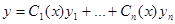однако в некоторых случаях частное решение у^* можно найти по виду функции f(x). Рассмотрим на примере неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами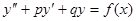

1) 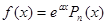где P_n(x) – многочлен n-ного порядка, a – действительное число.

а) если j(а) ¹ 0 т.е. а ¹ ни одному корню характеристического уравнения то 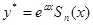где S_n(x) – многочлен той же степени n.

б) если j(а) = 0 т.е. а совпадает с одним из корней характеристического уравнения и имеет кратности (r=1 или 2) тогда 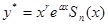далее поступать, как и пункте а).

Линейные однородные дифференциальные уравнения n^-го порядка.

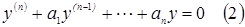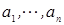, где - непрерывные функции переменной х или const.

Свойства:

(1).Если 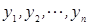решения однородного дифференциального уравнения (2) то их линейная комбинация с произвольными числами 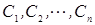, т. е. выражение 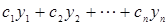также является решением дифференциального уравнения (2). Доказательство:Доказательство проведем для случая n=2, т. е. докажем что если у₁ и у₂ – решения дифференциального уравнения 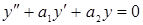то 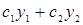также решения однородного дифференциального уравнения 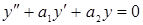. Т. к. 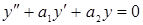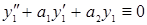у₁ и у₂ – решения дифференциального уравнения то и 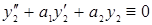. Покажем, что 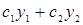удовлетворяет также однородному дифференциальному уравнению т. е.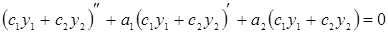

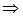
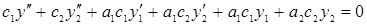или

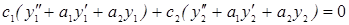
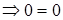. Аналогично доказывается и в общем случае n>2.

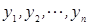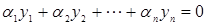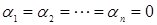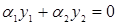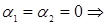Введем понятие линейно независимых и линейно зависимых функций и понятие вронскиана нескольких функций. Функции называются линейно независимыми на [a,b], если линейная комбинация , только если . Противном случае называется линейно зависимыми. В частности для n=2, у₁ и у₂ – линейно независимы если при линейно зависимы есл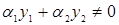и при 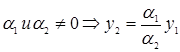- линейно зависимые и если 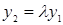, 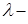любое действительное число 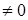то они линейно независимы.

Вронскиана функции 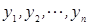называется определитель 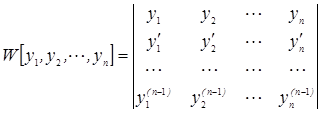, в частности 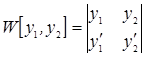свойства вронскиан: - Если функции 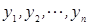линейно зависимы на [a,b] то их вронскиана =0 на [a,b]: для n=2; 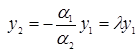и 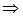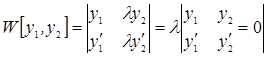на отрезке [a,b].

- Если функции 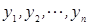- линейно независимы на отрезке [a,b], то их вронскиан 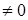на [a,b].

(2) Если 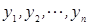- линейно независимые решения дифференциального уравнения 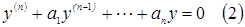то общее его решение у₀ дается выражением 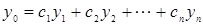, где 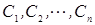- любые числа. Доказательство: Доказательство проведем для случая n=2, т. е. для дифференциального уравнения 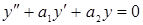докажем что 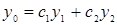общее решения. (а) 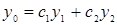– решение дифференциального уравнения 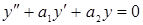по свойству (1). (б) Докажем, что 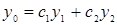общее решение однородного дифференциального уравнения т. е. удовлетворяет произвольным начальным условиям т. е. 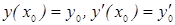отсюда следует 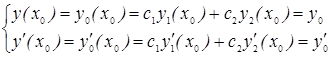эта система двух линейных неоднородных уравнений имеет единственное решение, если ее определитель 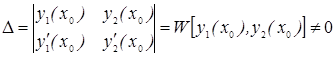, т. к. 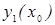и 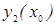- линейно независимы в точке х₀, таким образом общая структура общего решения линейного однородного дифференциального уравнения n-го порядка имеет вид

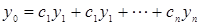, если 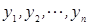линейно независимые решения.