С разделенными переменными

1.простейшие ДУ I порядка y’=f(x)

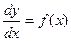=>dy=f(x)dx=> 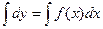=> 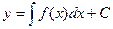, y₀=y(x₀)(можно найти частное решение.)

2.. Дифференциальное уравнение вида f(x)dx+φ(y)dy=0, где f(x), φ(y)-непрерывные функции то уравнение называется, уравнение с разделенными переменными

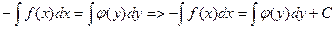получаем общее интегральное уравнение.

Уравнение с разделяющимися переменными.

2. ДУ вида M₁(x)*M₁(y)dx+ M₂(x)*M₂(y)dy=0, где М₁(х), М₁(у), М₂(х), М₂(у) – непрерывные функции это уравнение называется разделяющимися переменными (зависят отдельно только от х или у)

M₁(x)*M₁(y)dx+ M₂(x)*M₂(y)dy=0

Разделим на М₁(у) и М₂(х)

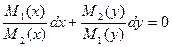- уравнение с разделенными переменными

Замечание:

Деление на М₂(х) и М₁(у) может:

1) привести к потери решений

М₂(х)=0, М₁(у)=0

2) уравнение с разделяющимися переменными можно привести к следующему виду:

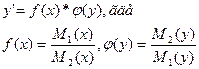
Опр. Функция f(x, y) называется однородной степени n если при любых α справедливо (λx. λy)=x^mf(x, y)f(x, y)=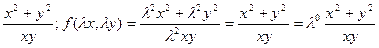

Однородное уравнение.

Однородное уравнение первого порядка f(x, y)-однородная степени 0.

Опр. ДУ первого порядка Р(х, у)dx+Q(x, y)dy=0(1) или уравнение 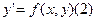если оно разрешается относительно 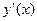называется однородным, если функции Р(х, у) и Q(x, y) однородные функции одной степени или f(x,y) – однородная функция нулевой степени однородное ДУ можно свести к уравнению с разделяющими переменными заменой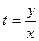

Правая часть (2) можно свести к аргументу 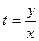, если положить 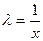степень однородности.

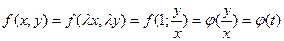т.к.f(x,y) однородная фун-ия

Выполним в уравнении (2) подстановку 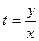; y=tx;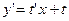

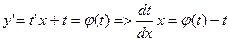(уравнение с разделяющими переменными)

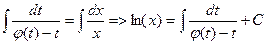общий интеграл ДУ (2)

Замечание: При разделении переменных полагаем, что 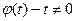, поэтому необходимо проверить особое решение.

Линейные

Опр. Линейным ДУ 1-го порядка называется уравнение линейное относительно неиз-ой функции и ее производной.

В общем случае оно может быть записано в виде

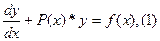где Р(х), f(x)-заданные непрерывные функции.

Если f(x)=0, то линейное уравнение называется однородным, в противном случае, неоднородное.

ЛОУ(линейное однородное уравнение)

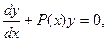уравнение с разделяющими переменными

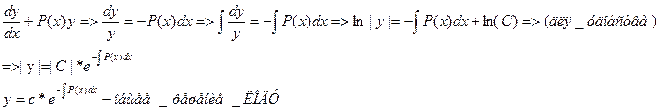Рассмотрим неоднородное ЛДУ:

для решение существует 2 метода:

1) метод Лагранжа(метод вариации постоянной)

Сначала решаем линейное однородное ДУ, соотв. неоднородному

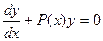=>решение 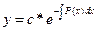С-не const, а неизвестная функция с=с(х)

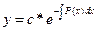-решаем (2)

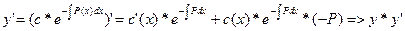подставим в (2)

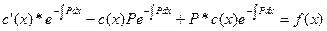
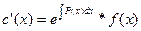уравнение с разделяющимися переменными

; ;

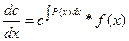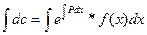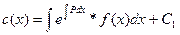
Решение ДУ

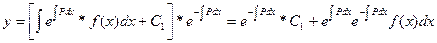
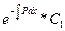-решение однородного ЛДУ(2)

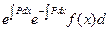-частное решение ДУ(2)

2)Метод Бернулли (метод подстановки)

Ищем решение ДУ (2) в виде произведения 2-х неизвестных функций.

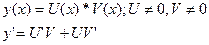
Подставим у, у' в (2)

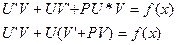
одну их неизвестных функций мы можем выбирать произвольным способом

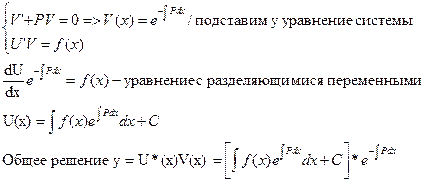
Уравнение Бернулли

y'+P(x)y=f(x)yⁿ, n≠0.1 (3)

t(x)=y^1-n (сводит к линейному уравнению)

t'=(1-n)y^-n y' преобразуем уравнение (3)

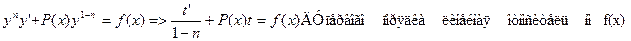
Уравнение Риккати

y'+P(x)y+Q(x)y²=f(x)

Заменяем z=z+y₁, где y₁ – частное решение уравнения Риккати, сводит его к уравнению Бернулли.

ДУ в полных дифференциалах.

ДУ вида M(x,y)dx+N(x,y)dy=0(4) называется уравнением полных дифференциалов если его левая часть представляет собой дифференциал от функции U(x,y) 2-x переменных M(x,y)dx+N(x,y)dy=dU(x,y)(4’)

Уравнение (4) dU(x,y)=0=>U(x,y)=C

Уравнение Лагранжа

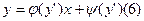
используется параметрический метод

y'=t, тогда (6)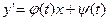

Дифференцируем по х

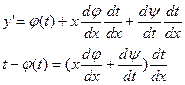
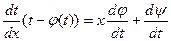
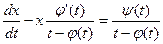-ЛДУ относительно х и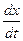

Решаем методом Лагранжа или методом Бернулли

тогда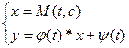

Замечание:

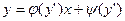
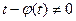, если 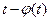=0 имеет действительные корни t=ti, то к общему решению нужно добавить 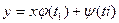, i=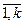

Уравнение Клеро (частный случай уравнения Лагранжа )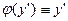

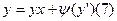
Пологаем y'=t, тогда 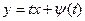дифференцируем по х и имеем:

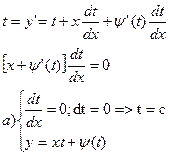
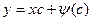-общее решение однопарамет-ое семейство прямых.

Замечание: сравнивая общее решение с 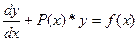получаем, что в исходном уравнении y' заменяем на производную константу.

б) x=φ’(t)=0

Решение оспаривется системой

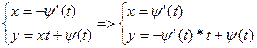
Замечание: интеграл Ф(x,y)=0 – особый интеграл

46. Определение общего решения ДУ порядка выше первого, частное решение.

Общим решением ДУ (1) называется функция y=φ(x, c₁, c₂,…,c_n) определенная в некоторой области изменения переменных x, c₁, c₂,…,c_n, имеющая непрерывные частные производные до n-го порядка, если:

1. она удовлетворяет условию (1) при любых x, c₁, c₂,…,c_n

2. Для заданных начальных условий: у₀=у(х), 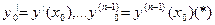можно подобрать значение констант С₁=С₀¹, С₂=С₀²,… С_n=С₀ⁿ, такие что функция y=φ(x, c₁, c₂,…,c_n) удовлетворяет условию (*)

Предлагается, что ( 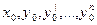) принадлежит области задания функции

Опр. Всякое общее решение, которое получается из общего решения при конкретном чис-х значений произвольных постоянных называется частным решением.

47. Теорема о существовании и единственности решения задачи Коши ДУ порядка выше первого (без док).

Если функция (n+1)-й переменной 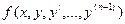в некоторой области (n+1)-мерного пространства непрерывна и имеет частную производную по переменной 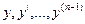, то для любой фиксированной точки 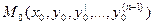этой области существует и при этом единственная, решение у=φ(х) уравнения 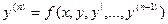определенное в некотором интервале, содержащее точку х₀ и удовлетворяет начальным условиям

у₀=у(х₀),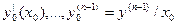

48. ДУ высших порядков, допускающие понижение порядка (3 типа).

Тип 1. уравнение вида y⁽ⁿ⁾=f(x)

Отличительной способностью такого уравнения является отсутствие в нем в явном виде самой искомой функции у и ее производных по (n-1)-го порядка включительно.

Решение такого уравнения находится путем последовательного интегрирования.

Тип 2. уравнение вида F(x;y^(n-1);y⁽ⁿ⁾)=0(например: y⁽⁴⁾=cos(x)-5*x)

Отличительной особенностью такого уравнения является отсутствие в нем самой функции у и ее младших производных до n-2-го порядка включительно. Такое уравнение сводится к уравнению первого порядка подстановкой у^(n-1)=z(x).

Частным случаем этого типа является уравнение второго порядка, не содержащее явно искомую функцию у: F(x;y’;y’’)=0. Подстановка у’=z(x); y’’= (у’)’=z’(x) приводит уравнение к уравнению первого порядка F(x;z(x);z’(x))=0

Решаем это уравнение, находим функцию z(x, C₁)=y’_x, а затем искомую функцию у(х;С₁;С₂)

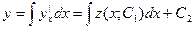(например: y’’*x*ln(x)-y’=0)

Тип 3. Уравнение второго порядка вида F(y;y’;y’’)=0

Характерной особенностью такого уравнения является отсутствие в нем в явном виде независимой переменной х. Порядок уравнения можно понизить до первого подстановкой

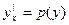, тогда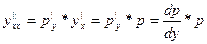

(В данном случае для нахождения у’’ используется правило дифференцирования сложной функции)(например: y’’=32*sin³(y)*cos(y))

49. Линейные ДУ n-го порядка.

Линейным дифференциальным уравнением высшего порядка называется уравнение, в котором искомая функция y(x) и ее производная входят в первых степенях и не перемножаются. Общий вод такого уравнения

a₀y⁽ⁿ⁾+a₁y^(n-1)+ a₂y^(n-2)+…a_ny=f(x), где а₀, а₁, … - либо функция от х, либо постоянные числа.

Линейное дифференциальное уравнение 2-го порядка имеет вид

ay’’+by’+cy=f(x).

Если f(x)=0, то уравнение называется однородным, уравнением без правой части. Если f(x)≠0, то уравнение называется неоднородным, или уравнением с правой частью.