Уравнения с разделенными и разделяющимися переменными
I. Дифференциальные уравнения первого порядка.
Дифференциальным уравнением первого порядка называется уравнение вида: F(t,x,x')=0 - алгебраическое выражение, содержащее функцию, её аргумент и первую производную функции. Также уравнение первого порядка может не содержать производной, в таком случае оно обязательно будет содержать дифференциал. Все слагаемые в выражении должны быть дифференциалами в таком случае:
dx+d(x+t)=0 - дифференциальное уравнение, а dx+x+t=0 дифференциальным уравнением не является.
Замечание: Часто люди, оставлющие здесь в разделе "дифференциальное уравнение" это элементарное определение забывают. Пишут уравнение с функцией и без производных/дифференциалов. Помните, чтобы мы вам могли помочь, мы должны понять вашу задачу. Старайтесь изъясняться с помощью общепринятого языка и понятий.
Решением дифференциального уравнения называется функция, при подстановке которой в исходное уравнение получается тождество. В общем случае, если решение существует, то существует целое множество решений дифференциального уравнения, образующее класс решений уравнения.
Среди дифференциальных уравнений первого порядка отдельно выделяют уравнения:
1. С разделёнными и разделяющимися переменными.
2. Однородные уравнения.
3. Линейные уравнения и уравнения Бернулли.
4. Уравнения в полных дифференциалах.
Описание и методы решения:
Уравнения с разделенными и разделяющимися переменными.
Уравнения с разделенными переменными - это самый простой класс уравнений первого порядка. Такие уравнения имеют вид:
1. 
2. 
Решение уравнений с разделенными переменными получается интегрированием правой и левой части:
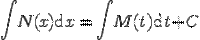
Пример:
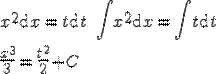
Последнее выражение - общий интеграл уравнения - алгебраическое выражение вида f(x,t,C)=0, выражающее зависимость x от аргумента t в неявном виде. C - произвольная константа.
***
Уравнения с разделяющимися переменными - уравнения вида:
1. 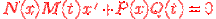
2. 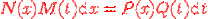
Решение этого класса уравнений можно получить, если свести их к уравнениям с разделёнными переменными, разделив на P(x)M(t):
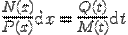
Следует помнить, что при делении на P(x)M(t) исходного уравнения можно потерять отдельный класс решений, соответствующих решению алгебраического уравнения P(x)M(t)=0. Эти решения называются особыми.
Пример:
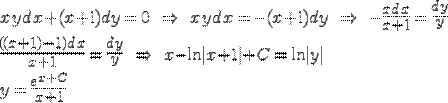
Особые решения: y(x)=0, x(y)=-1.
***
Следует помнить, что уравнения с разделенными и разделяющимися переменными не всегда будет сразу представлены в виде, представленном выше. Часто требуется произвести дополнительные операции - приведение подобных, вынос общего множителя за скобку, прочее.
Однородные уравнения.
Функция f(t,x) называется однородной, если 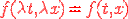 .
.
Однородное уравнение - уравнение вида 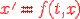 , где f(t,x) - однородная функция.
, где f(t,x) - однородная функция.
Решение этого класса уравнений сводится к решению уравнений с разделяющимися переменными следующим образом:
Положим в качестве 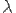
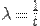 . Получим
. Получим
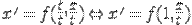
Положим x=t*u, тогда: 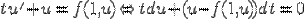 .
.
В некоторых случаях можно получить решение u(t,C) и, соответственно, x(t)=t*u(t,C). В других t(u,C) и x=t(u,C)*u (параметрическое семейство решений), C- произвольная константа.
***
Примеры:
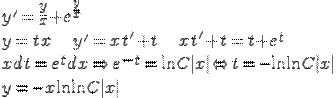
***
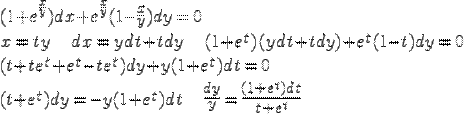
Линейные уравнения.
Линейное уравнение - это уравнение вида 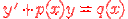 . Это уравнение можно решить следующими методами:
. Это уравнение можно решить следующими методами:
Метод Бернулли.
Суть метода состоит в разложении искомой функции на произведение двух других - 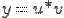 , и "подгонкой" их под нужный вид. В этом случае линейное уравнение будет сведено к системе из двух уравнений с разделяющимися переменными.
, и "подгонкой" их под нужный вид. В этом случае линейное уравнение будет сведено к системе из двух уравнений с разделяющимися переменными.
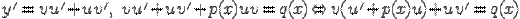 . Теперь нужно получить функцию
. Теперь нужно получить функцию 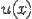 так, чтобы выражение
так, чтобы выражение 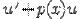 равнялось нулю. Для этого решим соответствующее уравнение с разделяющимися переменными
равнялось нулю. Для этого решим соответствующее уравнение с разделяющимися переменными 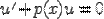 . Его решением будет
. Его решением будет 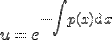 . Также стоит заметить, что функция u не зависит от произвольной постоянной. Теперь функцию
. Также стоит заметить, что функция u не зависит от произвольной постоянной. Теперь функцию  можно найти.
можно найти. 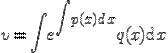 . Система уравнений, о которой я писал выше имеет вид:
. Система уравнений, о которой я писал выше имеет вид:
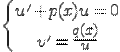
Решение исходного уравнения получим просто перемножив 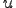 на
на 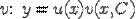
***
