А возможен, например, такой случай: нагрузка действует вниз, а балка почему-то прогибается не только вниз, но и вбок?
Да, такой случай возможен. Изгиб тогда называется косым. С этим случаем изгиба балки мы познакомимся подробнее в беседе 9. Косой изгиб возникнет в том случае, если силовая плоскость не совпадает ни с одной из главных плоскостей.
7.5. А какой изгиб называется плоским?
Нередко в учебной литературе прямой изгиб называют плоским изгибом. Последний термин, на наш взгляд, является не совсем удачным. И вот почему. Термины «прямой изгиб» и «косой изгиб» также легко сопоставляются, как и отдельные слова «прямо» и «косо». Сопоставлять же термины «плоский изгиб» и «косой изгиб» неправомерно, как, собственно, и слова «плоский» и «косой». Слову «плоский», скорее всего, можно было бы противопоставить слово «пространственный».
7.6. Какие внутренние усилия возникают в поперечном сечении балки при прямом изгибе?
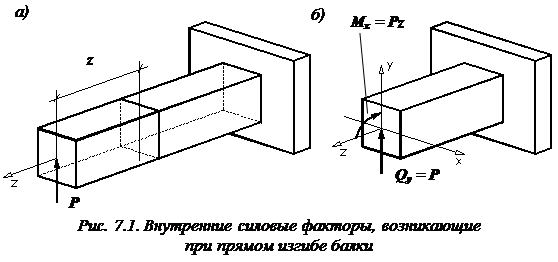
Рассмотрим, например, балку (рис. 7.1), нагруженную вертикальной сосредоточенной силой P.Для определения внутренних силовых факторов, возникающих в некотором поперечном сечении, расположенном на расстоянии z от места приложения нагрузки, воспользуемся методом сечений. Продемонстрируем два варианта использования этого метода, с которыми можно встретиться в учебной литературе.
Первый вариант.
Разрежем балку в намеченном нами поперечном сечении на расстоянии z от левого конца (рис. 7.1, а).
Отбросим мысленно правую часть балки вместе с жесткой заделкой (или просто, для удобства, закроем их листком бумаги).
Далее мы должны заменить действие отброшенной части на оставленную нами левую часть балки внутренними усилиями (силам упругости).Мы видим, что внешняя нагрузка пытается сместить видимую нами часть балки вверх (иными словами, осуществить сдвиг) с силой, равной P, а также изогнуть ее выпуклостью вниз, создавая момент, равный 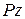 . Вследствие этого, в поперечном сечении балки возникают внутренние силы, которые оказывают сопротивление внешней нагрузке, то есть противодействуют и сдвигу, и изгибу. Эти силы, очевидно, возникают во всех точкахпоперечного сечения балки,ираспределены они по сечению по неизвестному пока нам закону. К сожалению, сразу же определить эту бесконечную систему сил невозможно. Поэтому мы сведем все эти силы к центру тяжести рассматриваемого поперечного сечения и заменим их действиестатически эквивалентными внутренними усилиями: перерезывающейсилой
. Вследствие этого, в поперечном сечении балки возникают внутренние силы, которые оказывают сопротивление внешней нагрузке, то есть противодействуют и сдвигу, и изгибу. Эти силы, очевидно, возникают во всех точкахпоперечного сечения балки,ираспределены они по сечению по неизвестному пока нам закону. К сожалению, сразу же определить эту бесконечную систему сил невозможно. Поэтому мы сведем все эти силы к центру тяжести рассматриваемого поперечного сечения и заменим их действиестатически эквивалентными внутренними усилиями: перерезывающейсилой  и изгибающиммоментом
и изгибающиммоментом 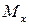 .
.
Как мы уже неоднократно отмечали выше, разрушение стержня в рассматриваемом сечении не произойдет только в том случае, если эти внутренние усилия  и
и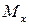 сумеют уравновесить внешнюю нагрузку. Поэтому мы легко находим, что
сумеют уравновесить внешнюю нагрузку. Поэтому мы легко находим, что 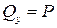 , а
, а 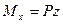 . Заметим, что именно благодаря этим двум внутренним усилиям
. Заметим, что именно благодаря этим двум внутренним усилиям  и
и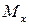 при разгрузке рассматриваемая нами часть балки опустится вниз и выпрямится.
при разгрузке рассматриваемая нами часть балки опустится вниз и выпрямится.
Второй вариант.
По-прежнемуразрежембалку в интересующем нас месте на две части. Но отбросим теперь не правую, а левую часть балки, нагруженную силой P. Заменим действие отброшенной нами части на оставленную правую часть стержня внутренними усилиями.Эти усилия мы найдем непосредственно как действие отброшенной левой части на правую часть. Для этого осуществим параллельный перенос силы P в центр тяжести рассматриваемого поперечного сечения балки (рис. 7.1, б). Согласно известной лемме из курса теоретической механики, сила, приложенная в какой-либо точке тела, эквивалентна такой же силе, приложенной в любой другой точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки ее приложения. Следовательно, в поперечном сечении стержня мы должны приложить силу P и момент 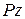 . Тогда перерезывающая сила
. Тогда перерезывающая сила 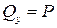 , а изгибающий момент
, а изгибающий момент 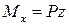 . То есть мы получаем тот же самый результат, но не производя процедуры уравновешивания.
. То есть мы получаем тот же самый результат, но не производя процедуры уравновешивания.
7.7. Какому из этих двух вариантов следует отдать предпочтение?
На наш взгляд, с методической точки зрения первый вариант лучше. И вот почему.
В первом варианте внутренние усилия  и
и 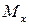 представляют собой статический эквивалент бесконечной системы внутренних сил, возникающих при изгибе балки в каждой точке ее поперечного сечения. И определяем мы эти внутренние усилия из условия, что, противодействуя внешней нагрузке, приложенной к рассматриваемой части стержня, они должны любой ценой ее уравновесить (иначе в этом поперечном сечении произойдет разрушение балки).
представляют собой статический эквивалент бесконечной системы внутренних сил, возникающих при изгибе балки в каждой точке ее поперечного сечения. И определяем мы эти внутренние усилия из условия, что, противодействуя внешней нагрузке, приложенной к рассматриваемой части стержня, они должны любой ценой ее уравновесить (иначе в этом поперечном сечении произойдет разрушение балки).
Во второмварианте внутренние усилия  и
и 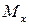 нами трактуются, по существу, как статический эквивалент не внутренних, а внешних сил, которые действуют на отбрасываемую часть стержня.
нами трактуются, по существу, как статический эквивалент не внутренних, а внешних сил, которые действуют на отбрасываемую часть стержня.
7.8. По каким правилам вычисляются изгибающий момент и перерезывающая сила, возникающие в поперечном сечении балки при изгибе?
Если мы используем первый вариант, то эти правила следующие:
1) перерезывающая сила численно равна алгебраической сумме всех внешних сил (активных и реактивных), действующих на рассматриваемую нами часть балки;
2) изгибающий момент численно равен алгебраической сумме моментов этих же сил относительно главной центральной оси, проходящей через центр тяжести рассматриваемого поперечного сечения.
Отметим, что изгиб, при котором в поперечном сечении балки возникают и изгибающий момент, и перерезывающая сила, называется поперечным. Если же в поперечном сечении балки возникает только изгибающий момент, то изгиб называется чистым.
