Глава 4.Основные принципы конструирования алгоритмов решения неустойчивых задач
Основные понятия и принципы.
Условно – корректнойназывается задача, решение которой для набора данных 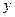 из множества
из множества 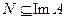 существует и единственно. Ее формальная запись:
существует и единственно. Ее формальная запись:
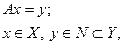 (4.1)
(4.1)
включает в себя: А – оператор, действующий из заданного функционального пространства Х в подмножество функционального пространства Y. По известному элементу у требуется найти элемент 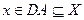 . Обратный к А оператор не имеет ограниченного обратного. Для того чтобы можно было оперировать понятиями нормы или модуля непрерывности обратного оператора, пространства
. Обратный к А оператор не имеет ограниченного обратного. Для того чтобы можно было оперировать понятиями нормы или модуля непрерывности обратного оператора, пространства  и
и 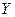 должны быть метрическими, в частности Банаховыми. Теория и методы решения условно корректных задач достаточно развиты [1-4]. Потребность в создании методов их решения существует в физике. Она возникла при интерпретации результатов физического эксперимента и, прежде всего, учета искажающих влияний измерительного канала. Эта же задача в геофизике определена в гл.1 как задача обработки наблюдаемых с целью редукции данных – наблюдаемых к физическим полям или их аналогам, пригодным для постановки обратных задач с целью реконструкции моделей среды. Используем введенные ранее обозначения:
должны быть метрическими, в частности Банаховыми. Теория и методы решения условно корректных задач достаточно развиты [1-4]. Потребность в создании методов их решения существует в физике. Она возникла при интерпретации результатов физического эксперимента и, прежде всего, учета искажающих влияний измерительного канала. Эта же задача в геофизике определена в гл.1 как задача обработки наблюдаемых с целью редукции данных – наблюдаемых к физическим полям или их аналогам, пригодным для постановки обратных задач с целью реконструкции моделей среды. Используем введенные ранее обозначения:  - это подлежащее определению и измеряемой с помощью аппаратуры модель физического поля
- это подлежащее определению и измеряемой с помощью аппаратуры модель физического поля 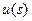 ;
;  - оператор, реализующий мультипликативное искажение с помощью аппаратной функции
- оператор, реализующий мультипликативное искажение с помощью аппаратной функции 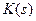 по правилу
по правилу 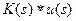 . В такой записи
. В такой записи 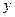 - некоторая идеализированная наблюдаемая
- некоторая идеализированная наблюдаемая 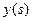 , которая реально осложнена аддитивной помехой
, которая реально осложнена аддитивной помехой 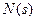 так, что реально имеется
так, что реально имеется 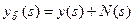 . Практически рассматриваемой моделью результатов измерений или, что то же самое, эталонироующих преобразований в содержательных обозначениях служит:
. Практически рассматриваемой моделью результатов измерений или, что то же самое, эталонироующих преобразований в содержательных обозначениях служит:
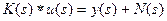 . . | (4.2) |
Элементы 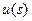 и
и 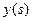 принадлежат известным нормированным пространствам
принадлежат известным нормированным пространствам  и
и 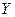 соответственно. Конкретная реализация погрешности
соответственно. Конкретная реализация погрешности 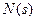 неизвестна, но она также считается некоторым элементом
неизвестна, но она также считается некоторым элементом 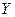 . По своей сути погрешность это то, что неизвестно. Для ее компенсации и учета необходимо вводить некоторые предположения и это, как всякие предположения о случайных величинах, суть предположения о ее статистических свойствах. К таковым относятся предположения о виде закона распределения либо его моментах, корреляционных функциях, спектральном составе и пр. Например, может быть введено предположение о том, что
. По своей сути погрешность это то, что неизвестно. Для ее компенсации и учета необходимо вводить некоторые предположения и это, как всякие предположения о случайных величинах, суть предположения о ее статистических свойствах. К таковым относятся предположения о виде закона распределения либо его моментах, корреляционных функциях, спектральном составе и пр. Например, может быть введено предположение о том, что 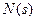 есть одна реализация эргодичного случайного процесса, обладающего свойствами белого шума – абсолютно некоррелированного процесса с нормальным распределением, нулевым средним и заданной величиной дисперсии. Совокупность статистических гипотез о том объекте, реализацией которого служит
есть одна реализация эргодичного случайного процесса, обладающего свойствами белого шума – абсолютно некоррелированного процесса с нормальным распределением, нулевым средним и заданной величиной дисперсии. Совокупность статистических гипотез о том объекте, реализацией которого служит 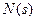 , обозначим
, обозначим 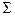 , а вся модель (2) обозначается
, а вся модель (2) обозначается 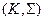 . Задача состоит в том, чтобы построить оператор
. Задача состоит в том, чтобы построить оператор 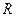 таким образом, чтобы, применив его задаче (2), получить в каком-то смысле наилучшее приближение к
таким образом, чтобы, применив его задаче (2), получить в каком-то смысле наилучшее приближение к 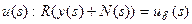 . Понятие наилучшего приближения требует конкретизации. Например, следует говорить лишь об определенном множестве
. Понятие наилучшего приближения требует конкретизации. Например, следует говорить лишь об определенном множестве 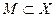 , на котором оператор
, на котором оператор 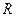 оптимален и характере оптимальности, например, обеспечивает наилучшее в квадратичном смысле приближение
оптимален и характере оптимальности, например, обеспечивает наилучшее в квадратичном смысле приближение 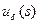 к
к 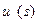 на
на 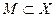 . Построение оператора
. Построение оператора 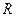 , который называется редукцией, во-первых, должно использовать статистические свойства помехи, в частности естественным представляется требование, состоящее в том, что расчетная невязка
, который называется редукцией, во-первых, должно использовать статистические свойства помехи, в частности естественным представляется требование, состоящее в том, что расчетная невязка 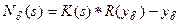 должна укладываться в статистическую гипотезу
должна укладываться в статистическую гипотезу 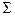 . Во-вторых, оно должно сопровождаться той либо иной формой введения априорной информации об искомом решении. Идеальная редукцияэто та, для которой
. Во-вторых, оно должно сопровождаться той либо иной формой введения априорной информации об искомом решении. Идеальная редукцияэто та, для которой 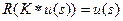 . Однако термин «идеальная», в данном контексте неадекватен действительности. Идеальная редукция, если она существует для всего
. Однако термин «идеальная», в данном контексте неадекватен действительности. Идеальная редукция, если она существует для всего  , совпадает с вычислением значений обратного оператора. Это задача неустойчивая и, как уже говорилось, мало толку от такого вычисления. Следует так конструировать редукцию, чтобы она, учитывая приближенность данных, давала согласованный с погрешностью устойчивый результат и этот результат стремился к точному по мере стремления погрешности к нулю. Такого типа приближенные, сходящиеся к точному значению редукции, называются регуляризованными приближениямик решению. Более строгие определения приводятся ниже. Рассмотрим теперь в качестве примеров некоторые характерные аппаратные функции
, совпадает с вычислением значений обратного оператора. Это задача неустойчивая и, как уже говорилось, мало толку от такого вычисления. Следует так конструировать редукцию, чтобы она, учитывая приближенность данных, давала согласованный с погрешностью устойчивый результат и этот результат стремился к точному по мере стремления погрешности к нулю. Такого типа приближенные, сходящиеся к точному значению редукции, называются регуляризованными приближениямик решению. Более строгие определения приводятся ниже. Рассмотрим теперь в качестве примеров некоторые характерные аппаратные функции 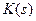 .
.
Интеграл Пуассона (2.6-2.6-а), преобразование Радона (2.9-10) доставляют примеры «аппаратных» функций 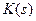 . Большое число примеров аппаратных функций можно найти в спектроскопии, где они называются иногда функциями щели (slit function). Эти функции конструируются как возможный отклик
. Большое число примеров аппаратных функций можно найти в спектроскопии, где они называются иногда функциями щели (slit function). Эти функции конструируются как возможный отклик 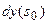 передающей системы в точке
передающей системы в точке 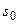 всего канала передачи информации на элементарный входной сигнал
всего канала передачи информации на элементарный входной сигнал 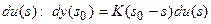 и зависят от некоторого параметра
и зависят от некоторого параметра 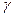 , характеризующего меру сглаживания, которую претерпел входной сигнал. Кроме того, из закона сохранения энергии следует, что должно выполняться условие нормировки:
, характеризующего меру сглаживания, которую претерпел входной сигнал. Кроме того, из закона сохранения энергии следует, что должно выполняться условие нормировки: 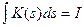

1. 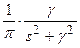 ; 2. ; 2. 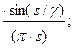 3. 3. 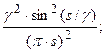 4. 4. 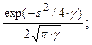 5. 5. 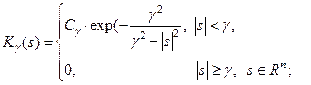 6. 6. 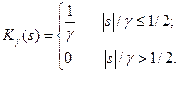 | 
|
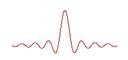
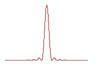
Все они обладают сглаживающими свойствами, и потому интуитивно очевидно, что идеальная реконструкция ведет к возрастанию присущих результату измерений осцилляций, связанных с погрешностями измерений -  . Какую из аппаратных функций использовать – часто дело субъективных предпочтений и в той либо иной степени убедительных аргументов в пользу преимущественных процессов, происходящих с сигналом при его прохождении по каналу, сопровождаемым размыванием, потерей резкости. Например, использование аппаратной функции (6) из (3) соответствует тому, что сигнал при прохождении канала усредняется с радиусом осреднения
. Какую из аппаратных функций использовать – часто дело субъективных предпочтений и в той либо иной степени убедительных аргументов в пользу преимущественных процессов, происходящих с сигналом при его прохождении по каналу, сопровождаемым размыванием, потерей резкости. Например, использование аппаратной функции (6) из (3) соответствует тому, что сигнал при прохождении канала усредняется с радиусом осреднения 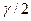 . Тогда задача (2) соответствует попытке реконструкции входного сигнала по его усредненным и зашумленным значениям. В аппаратной функции (1) из системы (3) легко увидеть ядро интеграла Пуассона, в котором роль параметра
. Тогда задача (2) соответствует попытке реконструкции входного сигнала по его усредненным и зашумленным значениям. В аппаратной функции (1) из системы (3) легко увидеть ядро интеграла Пуассона, в котором роль параметра 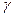 играет высота
играет высота 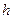 продолжения поля. Причем все функции 1-6 при стремлении параметра
продолжения поля. Причем все функции 1-6 при стремлении параметра 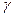 к нулю стремятся дельта функции Дирака и порождают единичное - тождественное преобразование. Поэтому на качественном уровне этот параметр можно уподобить некоторой эффективной «длине» канала, которую прошел распространяющейся по нему сигнал. Задача анализа данных может, в таком случае, состоять в расчете этой «эффективной длины», которая ассоциируется с интегральными свойствами канала, включающего в себя и изучаемую среду, по которому распространялся сигнал. Заданными служат выходной сигнал, предполагаемый входной (или его свойств, по достижении которых считается, что реконструкция входного завершена) и видом аппаратной – передаточной функции, например из класса (3). Новые аппаратные функции можно генерировать и подбирать сверткой приведенных, что соответствует объединению механизмов прохождения сигнала по разным каналам – использование составных каналов. В результате задача (1), и ее частный случай (2) являются весьма общими и имеют большое число разнообразных и интересных приложений. Следует обратить внимание и еще на то обстоятельство, что все аппаратные функции 1-5 похожи друг на друга при том, что аргументы и обоснование введения каждого из них весьма различны. Относительно небольшими возмущениями можно одну из них свести к другой, что в условиях их приближенности задания и последующей необходимости введения поправок для обеспечения устойчивых редукций, делает их результативно близкими друг к другу.
к нулю стремятся дельта функции Дирака и порождают единичное - тождественное преобразование. Поэтому на качественном уровне этот параметр можно уподобить некоторой эффективной «длине» канала, которую прошел распространяющейся по нему сигнал. Задача анализа данных может, в таком случае, состоять в расчете этой «эффективной длины», которая ассоциируется с интегральными свойствами канала, включающего в себя и изучаемую среду, по которому распространялся сигнал. Заданными служат выходной сигнал, предполагаемый входной (или его свойств, по достижении которых считается, что реконструкция входного завершена) и видом аппаратной – передаточной функции, например из класса (3). Новые аппаратные функции можно генерировать и подбирать сверткой приведенных, что соответствует объединению механизмов прохождения сигнала по разным каналам – использование составных каналов. В результате задача (1), и ее частный случай (2) являются весьма общими и имеют большое число разнообразных и интересных приложений. Следует обратить внимание и еще на то обстоятельство, что все аппаратные функции 1-5 похожи друг на друга при том, что аргументы и обоснование введения каждого из них весьма различны. Относительно небольшими возмущениями можно одну из них свести к другой, что в условиях их приближенности задания и последующей необходимости введения поправок для обеспечения устойчивых редукций, делает их результативно близкими друг к другу.
Среди большого числа частных схем устойчивого решения задачи (1) (относительно х) можно выделить присутствующие в них две главные идеи.
Первая из них состоит в том, что оператор А заменяется другим, близким к нему оператором 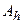 , но таким, что
, но таким, что 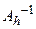 уже ограничен. В качестве оператора редукции
уже ограничен. В качестве оператора редукции 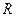 принимается
принимается 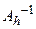 . Следует понимать, что близость А и
. Следует понимать, что близость А и 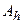 еще не означает, что для заданного у элементы x и
еще не означает, что для заданного у элементы x и 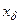 такие, что
такие, что 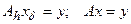 близки друг к другу. Тем более они могут весьма существенно различаться, если одно из уравнений рассматривается при приближенных, а втрое при точных данных (правых частях). Выявление таких условий, при которых эта близость имеет место, составляет один из главных предметов теории условно корректных задач. Методы, основанные на этой идее, называются методами квазиобращения.
близки друг к другу. Тем более они могут весьма существенно различаться, если одно из уравнений рассматривается при приближенных, а втрое при точных данных (правых частях). Выявление таких условий, при которых эта близость имеет место, составляет один из главных предметов теории условно корректных задач. Методы, основанные на этой идее, называются методами квазиобращения.
Другая идея состоит в том, что оператор А рассматривается лишь на некотором подмножестве М области определения DA и таком, что  непрерывен на
непрерывен на 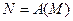 . Это будет иметь место, например, тогда, когда Х,Y- банаховы пространства и М- компакт. К этой группе относятся методы: регуляризации, рассмотренные методы квазирешений, связанные с ними методы приближенного вычисления значения неограниченного оператора. Четкой границы между этими подходами и различными методами внутри них нет. В большинстве реальных случаев они сводятся друг к другу так, что один и тот же метод может рассматриваться с точки зрения любой из этих идей. Различие трактовок и выбор одной из них по усмотрению подчеркивает наличие некоторой субъективности в принципах решения. Возможным это становится благодаря тому, что правая часть в (1) уже в постановочном плане рассматривается как осложненная ошибками. Следующие рассуждения поясняют сказанное.
. Это будет иметь место, например, тогда, когда Х,Y- банаховы пространства и М- компакт. К этой группе относятся методы: регуляризации, рассмотренные методы квазирешений, связанные с ними методы приближенного вычисления значения неограниченного оператора. Четкой границы между этими подходами и различными методами внутри них нет. В большинстве реальных случаев они сводятся друг к другу так, что один и тот же метод может рассматриваться с точки зрения любой из этих идей. Различие трактовок и выбор одной из них по усмотрению подчеркивает наличие некоторой субъективности в принципах решения. Возможным это становится благодаря тому, что правая часть в (1) уже в постановочном плане рассматривается как осложненная ошибками. Следующие рассуждения поясняют сказанное.
Пусть множество М, среди элементов которого ищется решение, имеет вид:
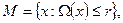
Где: r- заданное число; 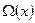 - некоторый функционал над Х. Например, таким образом может быть задано множество функций, имеющих ограниченную первую производную или ее полную вариацию на некотором множестве. Если у задано с ошибкой, то следует минимизировать величину невязки
- некоторый функционал над Х. Например, таким образом может быть задано множество функций, имеющих ограниченную первую производную или ее полную вариацию на некотором множестве. Если у задано с ошибкой, то следует минимизировать величину невязки 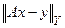 при условии, что
при условии, что 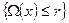 .Правило Лагранжа дает для этой задачи на условный минимум такую рекомендацию:
.Правило Лагранжа дает для этой задачи на условный минимум такую рекомендацию:
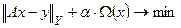 , (4.4)
, (4.4)
где  - число, называемое множителем Лагранжа, как-то связанной с величиной r. Уравнение Эйлера для (4) можно, с одной стороны, рассматривать как уравнение для решения в рамках второй идеи- оно из нее и было получено. Но оно же является и возмущением исходного уравнения до оператора с непрерывным обратным (если уравнение Эйлера непрерывно разрешимо) – в рамках первой идеи.
- число, называемое множителем Лагранжа, как-то связанной с величиной r. Уравнение Эйлера для (4) можно, с одной стороны, рассматривать как уравнение для решения в рамках второй идеи- оно из нее и было получено. Но оно же является и возмущением исходного уравнения до оператора с непрерывным обратным (если уравнение Эйлера непрерывно разрешимо) – в рамках первой идеи.
Элемент у всегда осложнен некоторой погрешностью 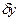 , которая подчинена статистике
, которая подчинена статистике 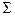 и является конкретной реализацией или просто иным обозначением введенной выше для модели (2) функции ошибок
и является конкретной реализацией или просто иным обозначением введенной выше для модели (2) функции ошибок 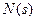 . Это реально заданная правая часть
. Это реально заданная правая часть 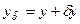 , из которой выделить «точную» часть невозможно. Так же с погрешностью задан и оператор A. Природа этой погрешности может быть самой разнообразной. Например, подбирая модель прохождения сигнала по каналу – аппаратную функцию, приходится делать многочисленные упрощающие дело предположения. Подобранная аппаратная функция будет иметь эффективный, эвристический характер (см. 1.3.). Другой пример – аппроксимация. При расчетах интегралов приходится вводить целую серию предположений, которые накапливаются в результирующие ошибки при расчетах на ЭВМ. Все это означает, что реально вместо оператора A используется оператор
, из которой выделить «точную» часть невозможно. Так же с погрешностью задан и оператор A. Природа этой погрешности может быть самой разнообразной. Например, подбирая модель прохождения сигнала по каналу – аппаратную функцию, приходится делать многочисленные упрощающие дело предположения. Подобранная аппаратная функция будет иметь эффективный, эвристический характер (см. 1.3.). Другой пример – аппроксимация. При расчетах интегралов приходится вводить целую серию предположений, которые накапливаются в результирующие ошибки при расчетах на ЭВМ. Все это означает, что реально вместо оператора A используется оператор 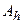 , и лучшее что мы о нем можем сказать, это то, что параметром h контролируется точность подгонки
, и лучшее что мы о нем можем сказать, это то, что параметром h контролируется точность подгонки 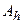 под A. Реально используемый оператор
под A. Реально используемый оператор 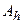 находится в h окрестности точного – A. Пара
находится в h окрестности точного – A. Пара 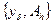 называется приближенными данными задачи, а пара (у,А) – ее точными данными. Таким образом для линейного оператора А параметры погрешности определены условием:
называется приближенными данными задачи, а пара (у,А) – ее точными данными. Таким образом для линейного оператора А параметры погрешности определены условием:
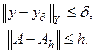
При этом 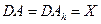 .
.
Ошибкой данныхназывается величина 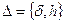 . Предполагается, что точным данным соответствует некоторое точное (гипотетическое) решение задачи (1). Необходимо приближенным данным
. Предполагается, что точным данным соответствует некоторое точное (гипотетическое) решение задачи (1). Необходимо приближенным данным 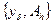 поставить в соответствие по некоторому правилу R -устойчивым образом элемент
поставить в соответствие по некоторому правилу R -устойчивым образом элемент 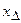 так, чтобы
так, чтобы 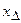 и х были в требуемом смысле близки друг другу. Правило редукции
и х были в требуемом смысле близки друг другу. Правило редукции 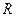 зависит, таким образом, не только от входных данных и вида оператора
зависит, таким образом, не только от входных данных и вида оператора 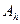 , но и от
, но и от 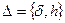 , которые являются параметрами семейства операторов редукции. Основу теории регуляризации составляют понятия регуляризующего алгоритма(оператора) и семейства регуляризующихоператоров. Приведем соответствующие определения.
, которые являются параметрами семейства операторов редукции. Основу теории регуляризации составляют понятия регуляризующего алгоритма(оператора) и семейства регуляризующихоператоров. Приведем соответствующие определения.
Обозначим 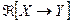 множество замкнутых линейных операторов из Х в Y. В частности по определению
множество замкнутых линейных операторов из Х в Y. В частности по определению 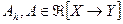 .
.
Определения.
1. Оператор 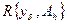 , определенный на паре элементов
, определенный на паре элементов 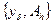 , действующий из
, действующий из 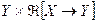 в Х, называется регуляризирующим алгоритмом (оператором) для задачи (1) в точке
в Х, называется регуляризирующим алгоритмом (оператором) для задачи (1) в точке 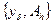 , если:
, если:
а) 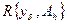 определен для всех
определен для всех 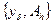 , являющихся приближенными данными задачи с заданными величинами
, являющихся приближенными данными задачи с заданными величинами 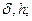 и
и 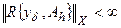 ;
;
b) 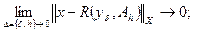 (4.5)
(4.5)
2. Если 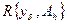 - регуляризирующий алгоритм (оператор) для всех
- регуляризирующий алгоритм (оператор) для всех 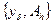 из некоторого множества данных
из некоторого множества данных 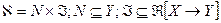 , то
, то 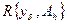 называется регуляризирующим алгоритмом на множестве
называется регуляризирующим алгоритмом на множестве 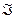 . Если оператор
. Если оператор 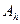 фиксирован, то при тех же условиях
фиксирован, то при тех же условиях 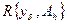 называется регуляризующим алгоритмом на
называется регуляризующим алгоритмом на 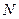 .
.
Последовательность регуляризирующих алгоритмов, параметризированных числовым параметром, зависящим от погрешности во входных данных должна давать результат, стремящийся к точным значениям при величинах погрешности стремящейся к нулю. Пусть α – числовой или векторный параметр, пробегающий некоторое множество Q. Параметрическое семейство операторов Rα называется регуляризирующим для задачи (1) в точке 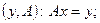 (точные дынные), если:
(точные дынные), если:
а) 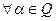 ,
, 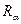 определен для любых:
определен для любых: 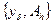 таких, что:
таких, что:
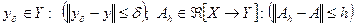 ;
; 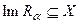 и
и 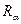 является регуляризующим алгоритмом;
является регуляризующим алгоритмом;
б) существует зависимость 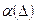 такая, что:
такая, что: 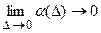
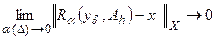 . (4.6)
. (4.6)
Таким образом, семейство регуляризующих операторов это такое их семейство, которое, будучи применено к входным данным приводит к решению, сходящемуся по мере уменьшения погрешности данных к гипотетическому точному решению. Это требование аналогично введенному выше (5), но учитывает то, что величина погрешности параметризует используемый регуляризующий алгоритм.
Однако следует еще учесть, что таких регуляризующих алгоритмов и семейств может быть много и все эти операторы 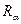 будучи применены к различным данным дают разную погрешность. Желательно, чтобы не только последовательность решений сходилась, но и эта погрешность была минимальной для каждого элемента из семейства, по сравнению с другими аналогичными семействами (по свойствам сходимости). Для этой цели вводится понятие оптимальных и оптимальных по порядку алгоритмов.
будучи применены к различным данным дают разную погрешность. Желательно, чтобы не только последовательность решений сходилась, но и эта погрешность была минимальной для каждого элемента из семейства, по сравнению с другими аналогичными семействами (по свойствам сходимости). Для этой цели вводится понятие оптимальных и оптимальных по порядку алгоритмов.
Погрешностью алгоритма 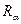 на классе
на классе  называется величина:
называется величина:
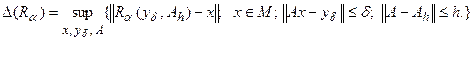 .
.
В приведенном определении погрешность это максимум того, что получается в разнице между точным и регуляризованным приближением при различных (а не фиксированных) 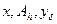 из множеств, определенных условиями окрестности. Метод
из множеств, определенных условиями окрестности. Метод 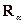 называется оптимальным, если величина доставляемой им погрешности
называется оптимальным, если величина доставляемой им погрешности 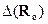 минимальна среди всех других алгоритмов:
минимальна среди всех других алгоритмов: 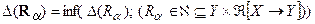 . Строгой оптимальности трудно добиться, поэтому используется более слабое условие – оптимальности по порядку. Алгоритм
. Строгой оптимальности трудно добиться, поэтому используется более слабое условие – оптимальности по порядку. Алгоритм 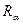 оптимален по порядку, если существует постоянная
оптимален по порядку, если существует постоянная 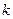 , что
, что 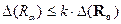 .
.
Квазиобращение.
Пусть А – линейный ограниченный оператор, действующий из гильбертова пространства Х в себя. Это существенное условие, ограничивающее область задач, которые могут решаться с помощью процедур квазиобращения. Предположим, что А – взаимно однозначен, самосопряженен, но  - неограничен. Если условие самосопряженности не выполняется, исходный оператор
- неограничен. Если условие самосопряженности не выполняется, исходный оператор  можно умножить на ему сопряженный
можно умножить на ему сопряженный 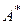 , перейдя к рассмотрению новой задачи с уже самосопряженным оператором
, перейдя к рассмотрению новой задачи с уже самосопряженным оператором 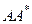 . При этом уравнение
. При этом уравнение 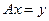 заменяется на
заменяется на 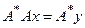 . Считаем далее, что такая замена, если в этом была необходимость, выполнена. Положим далее, что приближенные данные задачи (1)
. Считаем далее, что такая замена, если в этом была необходимость, выполнена. Положим далее, что приближенные данные задачи (1) 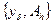 и ошибка данных –
и ошибка данных – 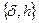 .
.
Конечномерный случай.
Пусть А – вещественная, симметричная положительная матрица размерности NхN. Тогда А имеет полную систему из N ортогональных собственных векторов 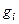 и соответствующую им систему собственных чисел
и соответствующую им систему собственных чисел 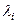 (с учетом их кратности). Для решения х задачи:
(с учетом их кратности). Для решения х задачи:
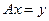 (4.7)
(4.7)
положим 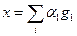 , где
, где 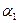 - неизвестные коэффициенты. Подставляя представление для х в (7), умножая скалярно результат на собственный вектор
- неизвестные коэффициенты. Подставляя представление для х в (7), умножая скалярно результат на собственный вектор 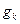 , и учитывая свойство ортогональности собственных векторов, легко получим:
, и учитывая свойство ортогональности собственных векторов, легко получим:
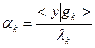 ,
,
и
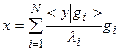 (4.8)
(4.8)
В представлении (8) хорошо видны проблемы, возникающие при решении неустойчивых задач. Неустойчивость задачи эквивалентна большой величине 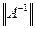 , что соответствует малой величине наименьших из собственных значений -
, что соответствует малой величине наименьших из собственных значений - 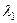 и в целом малости величин
и в целом малости величин  для некоторого множества индексов. Существенное значение имеют лишь оставшиеся индексы, образующие подмножество
для некоторого множества индексов. Существенное значение имеют лишь оставшиеся индексы, образующие подмножество 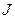 . Если расчеты делаются с идеальной точностью и также точно заданы: данные у, компонентные матрицы А, то при малой величине
. Если расчеты делаются с идеальной точностью и также точно заданы: данные у, компонентные матрицы А, то при малой величине  одновременно того же порядка малости окажутся и величины
одновременно того же порядка малости окажутся и величины 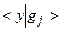 . Но фактически за счет разноплановости, несогласованности ошибок, присутствующих в разных элементах исходных данных, этого не произойдет. Произойдет, если так можно выразиться, “разбаланс” в малости величин
. Но фактически за счет разноплановости, несогласованности ошибок, присутствующих в разных элементах исходных данных, этого не произойдет. Произойдет, если так можно выразиться, “разбаланс” в малости величин 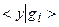 и
и  . Это, в свою очередь, приведет к тому, что при некоторых
. Это, в свою очередь, приведет к тому, что при некоторых  вклад в решение компоненты
вклад в решение компоненты 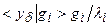 окажется неоправданно большим. Точным выражением для нее служит
окажется неоправданно большим. Точным выражением для нее служит 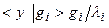 , а за счет ошибки в правой части (8) будем иметь
, а за счет ошибки в правой части (8) будем иметь 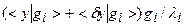 . Очень малой величине
. Очень малой величине  будет соответствовать согласованно малая величина
будет соответствовать согласованно малая величина 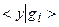 . Однако член
. Однако член 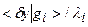 , за счет малости
, за счет малости  и конечности
и конечности 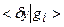 , может оказаться сколь угодно большим. Тогда вклад от величины
, может оказаться сколь угодно большим. Тогда вклад от величины 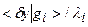 будет значительно большим, чем
будет значительно большим, чем 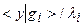 .
.
Итак, наличие малых собственных значений (конечно, в каждой конкретной задаче и конкретных данных вопрос о том, когда  уже чересчур мало, а когда еще не очень, решается индивидуально) приводи к неоправданно большому вкладу в решение компонент
уже чересчур мало, а когда еще не очень, решается индивидуально) приводи к неоправданно большому вкладу в решение компонент 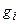 из набора собственных векторов с малыми собственными числами. Эта компонента оказывается столь большой, что “затушевывает” все остальное. Описанная ситуация типична. С небольшими вариациями она возникает при решении большинства неустойчивых задач. Однако формы борьбы с ней зависят от конкретных условий. Наилучшим выходом из создавшейся ситуации (без привлечения каких-либо еще сведений о решении) является определение по наблюдаемой
из набора собственных векторов с малыми собственными числами. Эта компонента оказывается столь большой, что “затушевывает” все остальное. Описанная ситуация типична. С небольшими вариациями она возникает при решении большинства неустойчивых задач. Однако формы борьбы с ней зависят от конкретных условий. Наилучшим выходом из создавшейся ситуации (без привлечения каких-либо еще сведений о решении) является определение по наблюдаемой 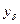 , исходя из (1), только части решения, точнее, тех компонент, которые определяются устойчиво. В этом и состоит один – первый из рассматриваемых подходов в теории решения некорректных (неустойчивых задач), который называется квазиобращением.
, исходя из (1), только части решения, точнее, тех компонент, которые определяются устойчиво. В этом и состоит один – первый из рассматриваемых подходов в теории решения некорректных (неустойчивых задач), который называется квазиобращением.
Заменим матрицу А близкой к ней, по такой, что в ней уже нет малых собственных значений. Например, в представлении (8) исключим первые суммы до ведичины 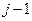 и запишем
и запишем
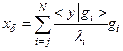 . (4.9)
. (4.9)
Последнее означает, что матрица А заменена другой - 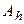 , определенной на подпространстве
, определенной на подпространстве 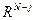 в
в  , ортогональном к собственным векторам
, ортогональном к собственным векторам 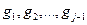 . Оценка уклонение А от
. Оценка уклонение А от 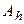 дает (из определения нормы оператора):
дает (из определения нормы оператора):
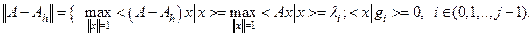 | (4.10) |
Итак, отображение 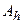 определено на подпространстве в
определено на подпространстве в  , образованного из множества индексов
, образованного из множества индексов 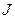 и уклоняется от А (определенном на всем
и уклоняется от А (определенном на всем  ) на величину, не превосходящую максимального из отброшенных собственных значений. Эта величина должна быть равной или быть меньшей априори заданной оценки погрешности h, с которой задан оператор A. Физически такой подход к регуляризации означает отказ от восстановления компонент модели, слабо выражающихся в поле, и восстановление с максимальной точностью устойчиво определяемых компонент. Однако такой подход к некорректным задачам требует разделения исходной задачи на две части: устойчивую и неустойчивую. В данном случае это разделение- решение проблемы на собственное значение и, в общем то субъективный анализ значимости отбрасываемых компонент. Это весьма трудная в вычислительном и смысловом отношениях проблема.
) на величину, не превосходящую максимального из отброшенных собственных значений. Эта величина должна быть равной или быть меньшей априори заданной оценки погрешности h, с которой задан оператор A. Физически такой подход к регуляризации означает отказ от восстановления компонент модели, слабо выражающихся в поле, и восстановление с максимальной точностью устойчиво определяемых компонент. Однако такой подход к некорректным задачам требует разделения исходной задачи на две части: устойчивую и неустойчивую. В данном случае это разделение- решение проблемы на собственное значение и, в общем то субъективный анализ значимости отбрасываемых компонент. Это весьма трудная в вычислительном и смысловом отношениях проблема.
В рамках рассматриваемого примера, если матрица А симметрична и положительна, можно другим образом регуляризовать задачу. Второй подход состоит в следующем. Добавим в знаменатель сумм в (8) некоторое малое положительно число
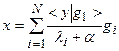 (4.11)
(4.11)
Если величина  достаточно мала (а малость ее должна быть согласована с малостью погрешности данных), то, не меняя существенно члены суммы в (8), где участвуют большие собственные значения
достаточно мала (а малость ее должна быть согласована с малостью погрешности данных), то, не меняя существенно члены суммы в (8), где участвуют большие собственные значения  , существенно уменьшается вклад членов с малыми собственными значениями. Здесь важно, чтобы собственные числа были величинами положительными. Иначе в знаменателе может оказаться ноль либо еще меньшее, чем изначально, значение. Описанный прием может быть обобщен и не требует решения проблемы на собственные значения. Действительно, если оператор А приведен к диагональному виду, то эквивалентным описанному приему является замена оператора А на
, существенно уменьшается вклад членов с малыми собственными значениями. Здесь важно, чтобы собственные числа были величинами положительными. Иначе в знаменателе может оказаться ноль либо еще меньшее, чем изначально, значение. Описанный прием может быть обобщен и не требует решения проблемы на собственные значения. Действительно, если оператор А приведен к диагональному виду, то эквивалентным описанному приему является замена оператора А на 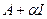 . В более общем случае можно говорить о замене оператора А на
. В более общем случае можно говорить о замене оператора А на 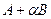 , где В - некоторый оператор со специальными, необходимыми для решаемой задачи свойствами. Оба из описанных приема трактуются в рамках уже описанной единой схемы:
, где В - некоторый оператор со специальными, необходимыми для решаемой задачи свойствами. Оба из описанных приема трактуются в рамках уже описанной единой схемы:
Оператор А заменяется близким к нему (в h- окрестности), но имеющим ограниченный обратный. На заданном элементе ищется значение оператора, обратного к этому приближенному. Именно эта схема называется квазиобращением [2].



 (4.3)
(4.3)