Задача на нахождение максимума
Задача № 3.1.
Решить симплексным методом задачу №1.1
Решение.
В задаче №1.1 построена модель задачи ЛП:
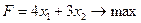 (3.1)
(3.1)
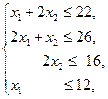 (3.2)
(3.2)
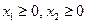 .
.
В задаче №2.1 приводится графическое решение данной задачи.
Для решения поставленной задачи симплексным методом от стандартной формы записи задачи ЛП перейдем к канонической. Ведем балансовые переменные 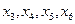 . Переменные
. Переменные 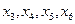 имеют экономический смысл: это остатки ресурсов
имеют экономический смысл: это остатки ресурсов 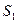 ,
, 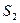 ,
, 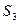 ,
, 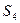 соответственно. Следовательно
соответственно. Следовательно 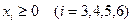 .
.
Каноническая форма записи системы (3.2):
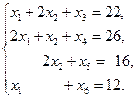 (3.3)
(3.3)
Составим расширенную матрицу системы (3.3):
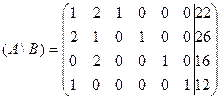
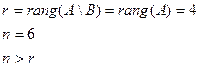
По теореме Кронекера - Капелли система (3.3) совместна и имеет бесчисленное множество решений.
Известно, что если задача ЛП имеет оптимальное решение, то оно совпадает, по крайней мере, с одним из опорных (допустимых базисных решений) системы (3.3). Так как ранг системы (3.3) равен четырем, то базисных переменных будет ровно четыре. На первом шаге в качестве базисных переменных удобно взять балансовые переменные 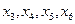 , так как система (3.3) легко разрешима относительно этих переменных.
, так как система (3.3) легко разрешима относительно этих переменных.
I. 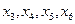 - базисные переменные;
- базисные переменные;
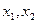 - свободные переменные.
- свободные переменные.
Систему (3.3) решим относительно базисных переменных:
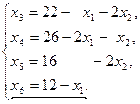 (3.4)
(3.4)
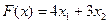 (3.5)
(3.5)
Обнулив свободные переменные, получим первое базисное решение:
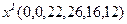 . Все компоненты полученного решения неотрицательны, следовательно,
. Все компоненты полученного решения неотрицательны, следовательно, 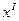 является опорным решением, при котором
является опорным решением, при котором 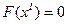 . По виду целевой функции (3.5) на данном шаге легко определить, что решение
. По виду целевой функции (3.5) на данном шаге легко определить, что решение 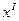 не является оптимальным, т.к. возможно дальнейшее увеличение целевой функции за счет введения в базис свободных переменных
не является оптимальным, т.к. возможно дальнейшее увеличение целевой функции за счет введения в базис свободных переменных 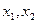 . При решении симплексным методом в базис свободные переменные вводятся поочередно. На данном шаге введем в базис переменную
. При решении симплексным методом в базис свободные переменные вводятся поочередно. На данном шаге введем в базис переменную 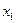 . Так как базисных переменных в системе (3.4) должно быть ровно четыре, то одну из переменных необходимо вывести из базиса.
. Так как базисных переменных в системе (3.4) должно быть ровно четыре, то одну из переменных необходимо вывести из базиса.
Предположим, что в системе (3.4) переменная 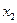 равна 0. Из первого уравнение системы (3.4) следует что, вводя
равна 0. Из первого уравнение системы (3.4) следует что, вводя 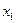 в базис, мы можем увеличить
в базис, мы можем увеличить 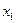 только до 22. При увеличении
только до 22. При увеличении 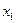 на значение большее, чем 22, переменная
на значение большее, чем 22, переменная 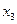 становится равной отрицательному числу, что противоречит смыслу задачи. Аналогично рассуждая, получим, что во втором уравнении системы (3.4)
становится равной отрицательному числу, что противоречит смыслу задачи. Аналогично рассуждая, получим, что во втором уравнении системы (3.4) 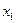 можно увеличить только до 13 единиц. В третьем уравнении увеличение
можно увеличить только до 13 единиц. В третьем уравнении увеличение 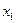 не повлияет на знак
не повлияет на знак 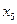 . В четвертом уравнении
. В четвертом уравнении 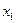 можно увеличить до 12 ед. Следовательно, при введении в базис
можно увеличить до 12 ед. Следовательно, при введении в базис 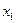 мы можем увеличить
мы можем увеличить 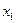 до значения
до значения 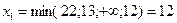 . Четвертое уравнение системы (3.4) на данном шаге является разрешающим. Разрешающее уравнение решим относительно
. Четвертое уравнение системы (3.4) на данном шаге является разрешающим. Разрешающее уравнение решим относительно 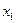 , тем самым введем
, тем самым введем 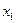 в базис, увеличив до 12 ед., а переменную
в базис, увеличив до 12 ед., а переменную 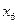 выведем из базиса. Получим
выведем из базиса. Получим 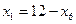 .
.
II. 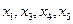 - базисные переменные;
- базисные переменные;
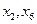 - свободные переменные.
- свободные переменные.
Систему (3.4) перепишем, заменив в каждом из уравнений 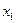 на выражение
на выражение 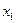 через свободные переменные:
через свободные переменные: 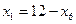 . Для контроля выполнимости критерия оптимальности, целевую функцию (3.5) также выразим через свободные переменные
. Для контроля выполнимости критерия оптимальности, целевую функцию (3.5) также выразим через свободные переменные 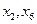 .
.
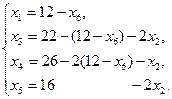
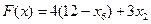 .
.
Приведя подобные члены в системе ограничений и в выражении целевой функции через свободные переменные, получим:
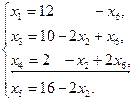 (3.6)
(3.6)
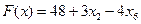 . (3.7)
. (3.7)
Обнулив свободные переменные, получим второе базисное решение:
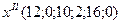 , которое также является опорным решением. Значение целевой функции увеличилось:
, которое также является опорным решением. Значение целевой функции увеличилось: 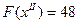 . Но решение
. Но решение 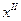 не является оптимальным, так как из (3.7) видно, что возможно дальнейшее увеличение
не является оптимальным, так как из (3.7) видно, что возможно дальнейшее увеличение 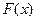 за счет увеличения свободной переменной
за счет увеличения свободной переменной 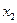 (введения
(введения 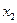 в базис).
в базис).
Увеличить 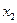 можно до значения
можно до значения 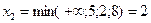 . Следовательно, третье уравнение системы (3.6) на данном шаге является разрешающим. Разрешающее уравнение решим относительно
. Следовательно, третье уравнение системы (3.6) на данном шаге является разрешающим. Разрешающее уравнение решим относительно 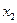 , тем самым введем
, тем самым введем 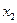 в базис, увеличив до 2 ед., при этом одновременно выведем из базиса
в базис, увеличив до 2 ед., при этом одновременно выведем из базиса 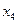 :
: 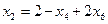 .
.
III. 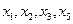 - базисные переменные.
- базисные переменные.
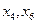 - свободные переменные.
- свободные переменные.
Систему (3.6) перепишем, заменив в каждом из уравнений 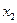 на выражение
на выражение 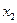 через свободные переменные:
через свободные переменные: 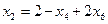 . Целевую функцию (3.7) также выразим через свободные переменные
. Целевую функцию (3.7) также выразим через свободные переменные 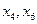 .
.
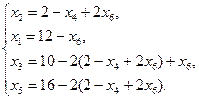
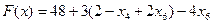 .
.
Приведя подобные члены в системе ограничений и в выражении целевой функции через свободные переменные, получим:
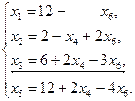 (3.8)
(3.8)
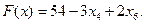 (3.9)
(3.9)
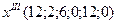 - третье опорное решение. Значение целевой функции увеличилось:
- третье опорное решение. Значение целевой функции увеличилось: 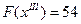 . Но решение
. Но решение 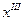 не является оптимальным, так как из (3.9) видно, что возможно дальнейшее увеличение
не является оптимальным, так как из (3.9) видно, что возможно дальнейшее увеличение 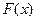 за счет увеличения свободной переменной
за счет увеличения свободной переменной 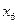 . Введем
. Введем 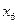 в базис, увеличив до значения
в базис, увеличив до значения 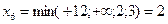 , при этом
, при этом 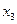 выведем из базиса.
выведем из базиса.
IV 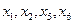 - базисные переменные.
- базисные переменные.
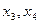 - свободные переменные.
- свободные переменные.
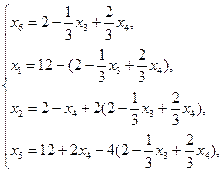
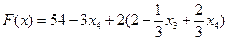 .
.
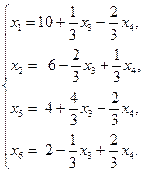 (3.10)
(3.10)
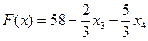 . (3.11)
. (3.11)
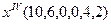 - четвертое опорное решение.
- четвертое опорное решение.
Полученное опорное решение будет оптимальным, так как все коэффициенты перед свободными переменными в выражении целевой функции (3.11) отрицательны и, следовательно, дальнейшее увеличение целевой функции невозможно. Отсюда: 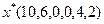 ,
, 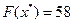 .
.
Ответ. Оптимальные объемы производства продукции 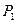 - 10 единиц; продукции
- 10 единиц; продукции 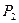 - 6 единиц. Ресурсы
- 6 единиц. Ресурсы 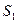 ,
, 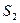 - израсходованы при оптимальном производстве полностью; ресурсы
- израсходованы при оптимальном производстве полностью; ресурсы 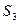 ,
, 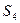 остались в количестве 4 усл. ед. и 2 усл. ед. соответственно. Прибыль, получаемая при реализации продукции, составила 58 д.е.
остались в количестве 4 усл. ед. и 2 усл. ед. соответственно. Прибыль, получаемая при реализации продукции, составила 58 д.е.
