Показатели безотказности
Л Е К Ц И Я
по дисциплине «Надежность вычислительных систем»
Тема № 1 «Основы теории надёжности»
Занятие №1.2 «Количественные показатели надежности»
1. Показатели безотказности
2. Показатели восстановления
3. Комплексные показатели
Введение.Типы объектов и режимы их эксплуатации
На состав показателей и построение моделей надежности существенное влияние оказывает тип объекта и режим его эксплуатации.
Тип объекта определяется решением, принимаемым после отказа. Если в рассматриваемой ситуации восстановление работоспособности конкретного объекта в случае его отказа признается невозможным (восстановление интегральной схемы), нецелесообразным по техническим или экономическим причинам (ремонт мышки) или неосуществимым (недоступный объекта – оборудование спутника на орбите), то такой объект является невосстанавливаемым в данной ситуации. Объекты данного типа могут иногда подвергаться восстановлению (ремонту, исправлению) вне места эксплуатации. Например, ошибки в исходном тексте программы устраняются разработчиком или организацией, ответственной за сопровождение программы, а исправленный файл с программой или "заплатка" передается пользователям для устранения дефекта.
Для восстанавливаемого объекта предполагается, что его работоспособность подлежит восстановлению при возникновении отказа в конкретных условиях эксплуатации. Под восстановлением понимается ремонт той или иной части объекта, замена частей на совершенно другие работоспособные части, а также в ряде случаев полная замена всего отказавшего объекта на новый работоспособный.
Один и тот же объект в зависимости от условий эксплуатации или ее этапов может считаться восстанавливаемым или невосстанавливаемым, например, электронное оборудование связного спутника при подготовке к запуску и после запуска на орбиту.
Режим эксплуатации определяет чередование периодов ожидания, когда по условиям эксплуатации объект не функционирует, но готов к немедленному приведению в действие, и периодов применения по назначению (периодов действия). Возникновение отказов и повреждений возможно в течение того и другого периодов, но во время периода ожидания расход ресурса объекта отсутствует или существенно меньше, чем во время периода применения. Кроме того, для многих типов устройств, в том числе и электронных, изменение режима эксплуатации более вредно для обеспечения безотказности, чем длительное нахождение в режиме применения (например, включение – выключение электропитания приводит к тепловым "ударам", изменяющим размеры электронных устройств и нарушающим их соединения, приводит к растрескиванию пайки и т.д.).
Возможны следующие основные виды режимов эксплуатации:
непрерывный. Период действия длится непрерывно в течение всего времени эксплуатации или продолжается достаточно длительное время. В этом случае время эксплуатации совпадает с календарным временем;
периодический. Периоды действия и простоя чередуются. Чередование может происходить с постоянной цикличностью или некоторым случайным образом. Периоды могут различаться и условиями эксплуатации. Наличие периодов простоя приводит к тому, что календарное время не совпадает с продолжительностью эксплуатации.
Показатели безотказности
Показатель надежности количественно характеризует одно или несколько свойств, составляющих надежность объекта, т.е. определяет в какой степени данному объекту присуще определенное свойство или свойства, обуславливающие надежность. Показатель надежности может иметь размерность (среднее время безотказной работы) или не иметь ее (вероятность безотказной работы).
Показатели надежности представляют в вероятностной или статистической форме. Вероятностная форма удобна для применения при аналитических расчетах, а статистическая – при экспериментальном исследовании надежности объекта. Кроме того, одни показатели проще интерпретировать в вероятностной форме, а другие – в статистической.
Применительно к невосстанавливаемым объектам статистические показатели формируются обычно исходя из такой схемы испытаний или эксплуатации объектов, при которой эти объекты работают с момента времени, равного нулю, до отказа. Продолжительность наработки до отказа считается случайной величиной. В этом случае статистические показатели надежности допускают простое частотное толкование. А с ростом количества испытываемых объектов статистические показатели будут сходиться к аналогичным вероятностным показателям.
Процесс эксплуатации восстанавливаемых объектов представляет собой в общем случае последовательность случайных интервалов работоспособности ti, чередующихся со случайными интервалами простоя τi. Математической моделью процесса эксплуатации является соответствующий случайный процесс. В общем случае функции распределения случайных величин t1, t2, … могут отличаться друг от друга. Это объясняется тем, что в очередной момент начала работы после восстановления объект характеризуется вполне определенным состоянием. Обычно рассматривают характеристики наработки до первого отказа и стационарные характеристики, т.е. характеристики стационарных случайных процессов, соответствующие времени, достаточно удаленному от начала эксплуатации. В последнем случае считается, что начальные состояния оказываются одинаковыми и наработки до очередного отказа имеют одинаковое распределение. Аналогично рассматриваются и характеристики времени восстановления. Практически во всех случаях предполагают независимость чередующихся величин ti и τi, а их распределение считают независимым от номера i. Такой случайный процесс получил название альтернирующего.
0 ti ti 
 ,
,
Рисунок 0.
При выборе номенклатуры показателей надежности и их определении следует руководствоваться государственными стандартами и другими нормативно-техническими документами [ГОСТ 27.001-95, Надежность АСУ 28.195-89]. В существующей НТД определено несколько десятков показателей надежности объектов, в какой-то мере различающихся по своему содержанию для технических и программных средств, а также для АСОИУ в целом. Эти показатели были первоначально сформированы для технических средств, а затем после появления таких объектов как автоматизированные системы нашли применение для характеристики надежности других компонентов этих систем. Рассмотрим сначала традиционное представление показателей надежности невосстанавливаемых и восстанавливаемых объектов. Сами показатели, если не касаться причин возникновения отказов и содержательной стороны процессов функционирования и восстановления, полностью применимы для любых изделий.
Невосстанавливаемые объекты работают до первого отказа. Основными показателями надежности таких объектов являются показатели безотказности. Рассмотрим вероятностное и статистическое определение показателей.
Вероятность безотказной работы в интервале от 0 до t0. Эта вероятность сопоставляется с заданной наработкой, в течение которой возможно возникновение отказа. При этом предполагается, что в начальный момент времени исчисления наработки объект был работоспособным (рисунок 1).
Вероятностное определение соответствует вероятности P(t0) того, что объект проработает безотказно в течение времени t0, начав работать в момент времени t = 0, или вероятность того, что наработка до отказа окажется больше заданного времени работы
| P(t0) = P(0, t0) = P(x> t0) = 1 – F1(t0), | (1а) |
где F1(t0) – функция распределения времени до первого отказа;
x – случайная наработка объекта до первого отказа.
Статистическое определение соответствует частости события, состоящего в том, что время работы изделия до отказа окажется больше заданного времени работы t0
| P*(t0) = N(t0) / N(0) = 1 – n(t0) / N(0), | (1б) |
где N(t0) – количество объектов,безотказно проработавших до момента t0;
N(0) – количество объектовработоспособных в начальный момент времени t = 0;
n(t0) – количество изделий, отказавших к моменту времени t0.
0 t tО 
 ,
,
Рисунок 1.
где tО 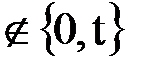 - момент возникновения отказа.
- момент возникновения отказа.
Конкретное численное значение вероятности безотказной работы имеет определенный смысл лишь тогда, когда оно поставлено в соответствие заданной наработки, в течение которой возможно возникновение отказа. Вероятность безотказной работы определяется в предположении, что в начальный момент времени исчисления заданной наработки, элемент был работоспособен. Для этого обозначим символом Х конкретное значение случайной величины времени безотказной работы элемента (или его наработку). Тогда количественно безотказность элемента можно характеризовать величиной вероятности того, что время его безотказной работы будет больше заданного t (рассматриваемого) промежутка времени.
Обозначим вероятность безотказной работы элемента за заданный интервал времени t через P(t), тогда
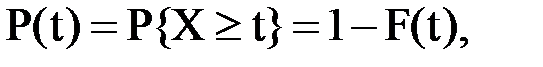
где F(t) – функция распределения наработки до первого отказа.
Вероятность безотказной работы элемента часто называют функцией надежности.
В ряде случаев удобно использовать понятие ненадежности элемента, характеризующее потерю работоспособности элементом. Ненадежность измеряется вероятностью того, что время безотказной работы Х будет меньше заданного интервала времени t.
Обозначим вероятность появления отказа на интервале времени t через q(t). Тогда:
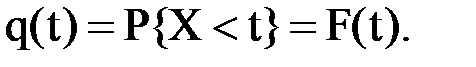 (2)
(2)
Вероятность появления отказа элемента часто называют функцией ненадежности.
Вероятность отказа объекта в интервале времени от 0 до t0 определяется как дополнительная к вероятности безотказной работы
| Q(t0) = 1 – P(t0) ≈ 1 – P*(t0). | (2б) |
Эта величина характеризует вероятность того, что время наработки до отказа будет меньше заданного значения. Поэтому вероятность отказа по своему смыслу соответствует значению функции распределения времени наработки до отказа.
Основными свойствами функции надежности являются:
1. Функция p(t) является монотонно убывающей функцией времени, т.е. при t2>t1 p(t2)<p(t1);
2. 0 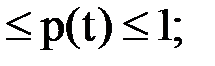
3. При t=0 р(0)=1; lim p(t) =0.
t 
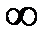
Таким образом, значение этой количественной характеристики надёжности ВС изменяется в пределах от 1 до 0, уменьшаясь с увеличением рассматриваемого интервала времени t.
Учитывая взаимосвязь функций p(t) и q(t), отметим, что функция q(t) также монотонная, но возрастающая функция времени, для которой справедливы следующие свойства:
1. При t2 >t1 , q(t2)>q(t1) ;
2. 0 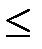 q(t)
q(t) 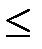 1;
1;
3. q(0)=0 и q( 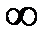 )=1.
)=1.
Вид зависимостей вероятности безотказной работы и вероятности отказа от времени показаны на рисунке 2.
p(t),q(t)
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
1
| q(t)
|
|
| |
| | p(t)
| |
| |
0 t1 t2 t
Рисунок 2.
Вероятность безотказной работы объекта P(t, t + t0) в интервале времени от t до t+ t0 рассматривается как условная вероятность.
Вероятностное определение P(t, t + t0) можно дать двумя способами:
как вероятность того, что объект будет безотказно работать до момента времени t+ t0, начиная с момента времени t;
как условную вероятность того, что случайная наработка объекта до отказа будет больше величины t + t0 при условии, что объект уже проработал безотказно до момента времени t.
Следовательно, вероятностное определение
| P(t, t + t0) = P(Х ³ t + t0 | Х> t) = P(0, t + t0) / P(0, t) = P(t + t0) / P(t). | (3а) |
Статистическое определение соответствует отношению количества объектов, проработавших безотказно до момента времени t + t0 к количеству объектов, исправных к моменту времени t, или частости события, состоящего в том, что реализация наработки объект до отказа окажется больше t + t0 при условии, что эта реализация больше времени t
| P*(t, t + t0) = N(t + t0) / N(t). | (3б) |
Вероятность отказа объект в интервале времени от t до t+ t0 определяется как дополнительная к соответствующей величине
| Q(t, t + t0) = 1– P(t, t + t0) = [P(t) – P(t + t0)] / P(t,). | (4) |
Функция q(t), в силу определений, принятых в теории вероятностей, является интегральным законом распределения случайной величины времени безотказной работы ВС и является её исчерпывающей характеристикой. Однако на практике, для удобства инженерных расчетов пользуются дифференциальным законом распределения.
В рассматриваемом случае для времени безотказной работы элемента функция дифференциального закона f(t) распределения её значений связано с интегральным законом соотношением f(t)= 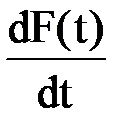 =
= 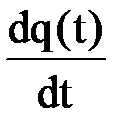 = -
= - 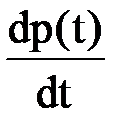 , поскольку q(t)=1-p(t).
, поскольку q(t)=1-p(t).
Функцию f(t) называют ещё плотностью распределения вероятностибезотказной работы или просто плотностью распределения. Рассматривая функцию f(t), нельзя не заметить, что
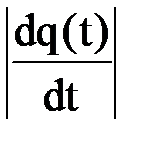 =
= 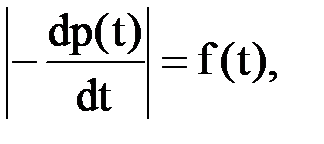 (5а)
(5а)
то есть плотность распределения возможности появления отказа и возможности безотказной работы равны друг другу с точностью до знака. Графическая интерпретация данной зависимости показана на рисунке 3. Учитывая что случайная величина времени безотказной работы элемента (объекта) лежит в пределах 0£ Х<¥, то имеет место соотношение 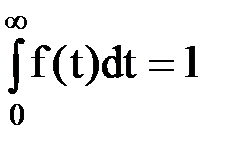
Пользуясь f(t), можно вычислить вероятности различных событий.
P(t),q(t)
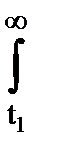 f(t)dt=р(t) f(t)dt=р(t) |

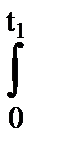 f(t)d(t)=q(t) f(t)d(t)=q(t) |
| t1 |
| t |
Рисунок 3.
Статистическое определение соответствует отношению количества отказов в интервале времени [t + Δt] к произведению количества исправных объектов в начальный момент времени t = 0 на длительность интервала времени Δt (величина Δt достаточно малая)
| f*(t) = [n(t + Δt) – n(t)]/[N(0) Δt] = [N(t) – N(t +Δt)]/[ N(0) Δt]. | (5б) |
Вероятности появления отказа и безотказной работы на интервале (0, t), с начала эксплуатации элемента (объекта) до момента t будут соответственно:
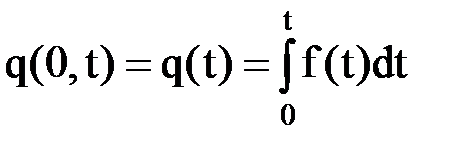 (5в)
(5в)
и
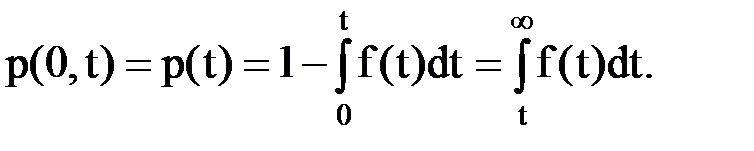 (5г)
(5г)
Графическая интерпретация последнего случая представлена на рис. 3. Таким образом, функция f(t) плотности распределения вероятности безотказной работы является вполне исчерпывающей количественной характеристикой безотказности ВС, позволяющей перейти от нее к другим ранее введенным количественным характеристикам. Это положение будет справедливо и для других количественных характеристик надежности, которые будут рассмотрены ниже.
Средняя наработка до отказа - величина T0 характеризует время безотказной работы ВС до момента возникновения отказа и представляет собой математическое ожидание их наработки до первого отказа. Согласно теории вероятности математическое ожидание случайной величины Т0 в предположении, что известен закон распределения плотности вероятности безотказной работы элементов ВС будет определяться следующим выражением

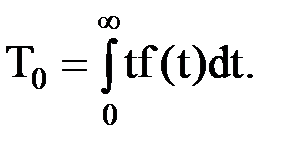 (6)
(6)
Поскольку
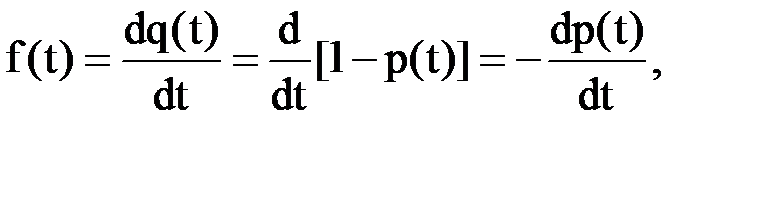

то f(t)dt = -dp(t). Тогда 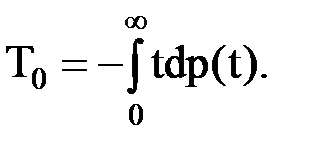 (7)
(7)
Интегрируя по частям, получим
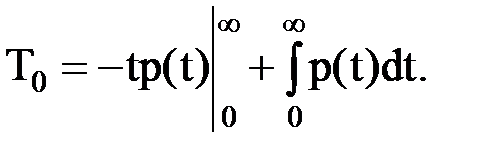
Учитывая, что p(0)=1,а p(¥)= 0, приходим к выводу, что в практически встречающихся случаях
Tp(t) 
 =0,
=0,
так как 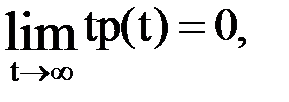 что следует из ограниченности срока службы элементов ВС. Таким образом, окончательно получим, что
что следует из ограниченности срока службы элементов ВС. Таким образом, окончательно получим, что
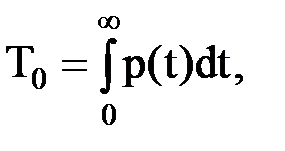 (8)
(8)
из чего следует, что средняя наработка до отказа численно равна площади, ограниченной функцией вероятности безотказной работы и осями координат, что используют в некоторых инженерных расчетах (см. рисунок 4).
Статистическая оценка для средней наработки до отказа определяется формулой:
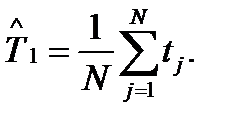 (9)
(9)
Здесь N – число работоспособных элементов ВС при t=0;
tj– наработка до первого отказа каждого из элементов.
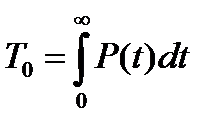 |
0 t
Рисунок 4
Средняя наработка на отказ То - отношение наработки восстанавливаемой ВС к математическому ожиданию числа его отказов в течение этой наработки. Этот показатель введен применительно к восстанавливаемым объектам, при эксплуатации которых допускаются многократно повторяющиеся отказы. Очевидно, что это должны быть несущественные отказы, не приводящие к серьезным последствиям и не требующим значительных затрат на восстановление работоспособного состояния. Эксплуатация таких объектов может быть описана следующим образом: в начальный момент времени объект начинает работать и продолжает работать до первого отказа; после отказа происходит восстановление работоспособности, и объект вновь работает до отказа и т. д. На оси времени моменты отказов образуют поток отказов, а моменты восстановлений – поток восстановлений. На оси суммарной наработки (когда время восстанавливания не учитывается) моменты отказов образуют поток отказов. Полное и строгое математическое описание эксплуатации объектов по этой схеме построено на основе теории восстановления.
Определению средней наработки на отказ Т, которое приведено в данном стандарте, соответствует следующая формула
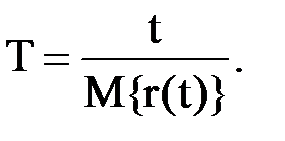 (10)
(10)
Здесь t – суммарная наработка, r(t) – число отказов, наступивших в течение этой наработки, M{r(t)} – математическое ожидание этого числа. В общем случае средняя наработка на отказ оказывается функцией t. Для стационарных потоков отказов средняя наработка на отказ от t не зависит.
Статистическую оценку средней наработки на отказ 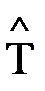 вычисляют по формуле
вычисляют по формуле
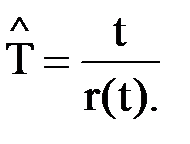 (11)
(11)
Следующим по важности показателем является интенсивность отказов. Интенсивность отказов ( 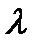 (t)) - условная плотность вероятности возникновения отказа невосстанавливаемого объекта, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не возник. Понятие интенсивность отказов удобнее всего ввести в связи с рассмотрением так называемой условной вероятности безотказной работы элемента. Во многих случаях приходится определять вероятность безотказной работы элемента за период времени от t1 до t2 при условии, что к началу рассматриваемого отрезка времени (t1,t2) элемент не отказал.
(t)) - условная плотность вероятности возникновения отказа невосстанавливаемого объекта, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не возник. Понятие интенсивность отказов удобнее всего ввести в связи с рассмотрением так называемой условной вероятности безотказной работы элемента. Во многих случаях приходится определять вероятность безотказной работы элемента за период времени от t1 до t2 при условии, что к началу рассматриваемого отрезка времени (t1,t2) элемент не отказал.
Вычисленная при таких условиях вероятность безотказной работы (или вероятность отказа) называется условной. Будем обозначать условную вероятность безотказной работы на отрезке времени (t1,t2) через р(t1,t2/t1) и найдем соотношение, определяющее величину условной вероятности безотказной работы элемента. Для этого рассмотрим два отрезка (t0,t1) и (t1,t2) на оси времени и связанные с ними события А и В, показанные на рисунке 5.
А В
t
t0 t1 t2
Рисунок 5
Событие А состоит в том, что элемент безотказно работает на отрезке времени (0,t1).Вероятность выполнения этого события обозначим
Р{А}=p(0,t1)=p(t1). (12)
Событие В состоит в том, что элемент безотказно работает на отрезке времени (t1,t2) при условии, что событие А совершилось. Вероятность выполнения события В обозначим
Р{B}=p(t1,t2/A)=p(t1,t2/t1). (13)
Тогда событие С, состоящее в том, что элемент безотказно проработает на отрезке времени от t0 до t2,будет выполняться с вероятностью, соответствующей вероятности совместного наступления событий А и В. Следовательно,
Р{C}=Р{А  В}=p(0,t2)=p(t2)=p(t1)
В}=p(0,t2)=p(t2)=p(t1)  p(t1,t2/t1), откуда p(t1,t2/t1) =
p(t1,t2/t1), откуда p(t1,t2/t1) =  Р(t2)/P(t1)
Р(t2)/P(t1)
Условная вероятность отказа элемента за период времени от t1 до t2 будет
q(t1,t2/t1)=1-p(t1,t2/t1)=1- P(t2)/(t1)=(P(t1) - P(t2))/P(t1)
Рассмотрим условную вероятность отказа на элементарном отрезке  t, которую запишем в виде
t, которую запишем в виде
q(t,t+  t/t)=(P(t)-P(t+
t/t)=(P(t)-P(t+  t))/ P(t)
t))/ P(t)
Умножим числитель и знаменатель правой части последнего выражения на  t и возьмём предел от него при
t и возьмём предел от него при  tà0, тогда
tà0, тогда
lim q (t,t+  t/t)= -[P(t+
t/t)= -[P(t+  t)-P(t)]/
t)-P(t)]/  t * (
t * (  t/P(t)) = dp(t)/dt*dt*1/p(t)=p’(t)*dt/p(t)
t/P(t)) = dp(t)/dt*dt*1/p(t)=p’(t)*dt/p(t)
 tà0
tà0
Обозначим 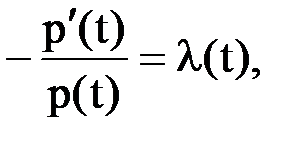 тогда получим
тогда получим
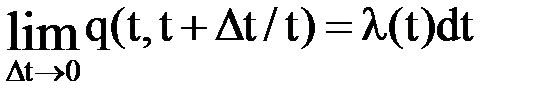 .
.
При рассмотрении безусловной вероятности отказа элемента, мы считаем, что

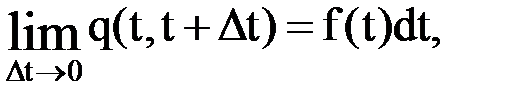
где f(t) – безусловная плотность распределения вероятности безотказной работы элемента.
Окончательно получим
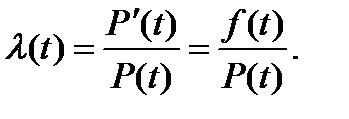 (14)
(14)
Эту функцию называют интенсивностью отказов.
Продолжим вывод выражения, определяющего условную вероятность безотказной работы.
Установили, что
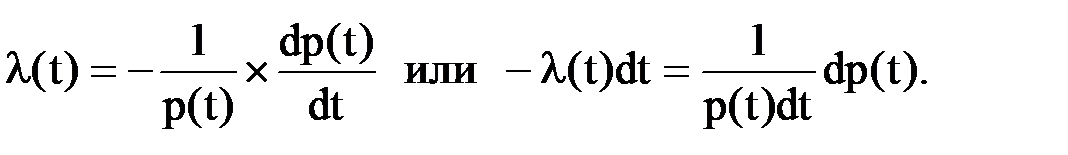
Взяв интеграл в пределах от t1 до t2 от обеих частей записанного равенства, получим
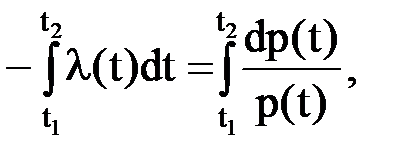
откуда путем несложных преобразований придем к соотношению
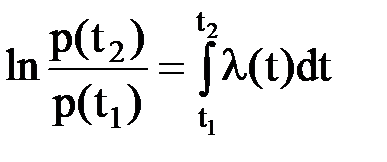
или
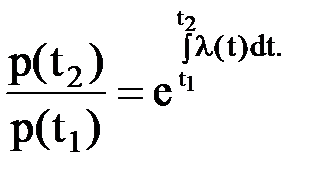
Но ранее было показано, что отношение p(t2)/p(t1) является условной вероятностью безотказной работы элемента на отрезке времени от t1 до t2 следовательно,
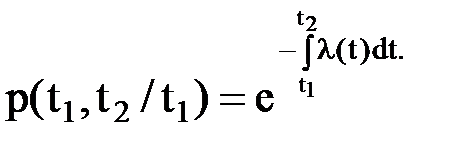
Если t1=0, то p(t1)=1 и полученное выражение можно записать в виде
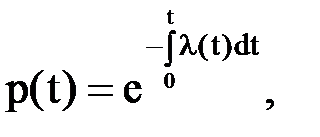 (15)
(15)
где t – произвольный промежуток времени, начинающийся с нуля.
Эту формулу для определения условной вероятности безотказной работы называют основной формулой надежности. Особенностью этой формулы является тот факт, что при выводе ее не оговаривается вид закона распределения случайных значений времени безотказной работы. А это значит, что последнее соотношение справедливо при любом законе распределения времени безотказной работы элементов.
Функция 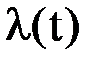 интенсивности отказов является важной количественной характеристикой безотказности элементов вычислительной средств.
интенсивности отказов является важной количественной характеристикой безотказности элементов вычислительной средств.
Во многих практических случаях изменение функции 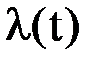 во времени происходит так, как показано на рисунке 6, где имеют место три характерных участка.
во времени происходит так, как показано на рисунке 6, где имеют место три характерных участка.
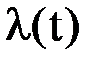
I II III
0 t1 t2 t
Рисунок 6
Понижение 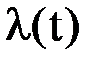 на участке I связано с наличием скрытых дефектов в элементах на начальном этапе их эксплуатации и исключением из серии элементов, поставленных на опытную эксплуатацию, и элементов, имеющих дефекты.
на участке I связано с наличием скрытых дефектов в элементах на начальном этапе их эксплуатации и исключением из серии элементов, поставленных на опытную эксплуатацию, и элементов, имеющих дефекты.
Участок I называют этапом (участком) приработки.
Участок II характерен тем, что интенсивность отказов примерно постоянна. Это этап нормальной эксплуатации.
Участок III обусловлен тем, что в силу необратимых процессов элементы изменяются, параметры, характеризующие их качество, выходят за пределы допустимых значений, все это приводит к увеличению интенсивности отказов. Этот участок называют этапом старения или износа элементов. Несмотря на общность характера изменения 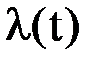 продолжительность указанных этапов для различных элементов вычислительных средств разная.
продолжительность указанных этапов для различных элементов вычислительных средств разная.
Знание любой одной из рассмотренных функции позволяет определить остальные, табл. 1.
Таблица 1
| Определяемый показатель надежности | Известный показатель надежности | |||
| Р(t) | Q(t) | f(t) | λ(t) | |
| Р(t) | Р(t) | 1 – Q(t) | 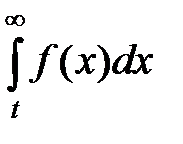 | 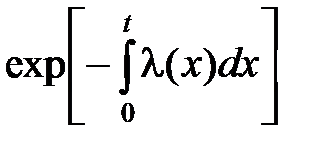 |
| Q(t) | 1 – Р(t) | Q(t) | 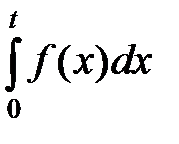 | 1– 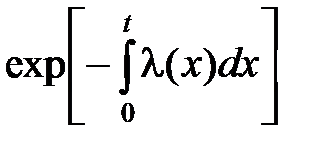 |
| f(t) | – dP(t)/dt | dQ(t)/dt | f(t) | 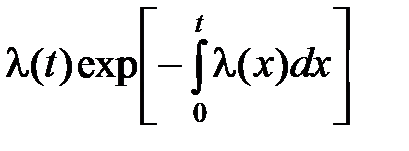 |
| λ(t) | –d[lnP(t)]/dt | dQ (t)/dt /[1–Q(t)] | f(t) / 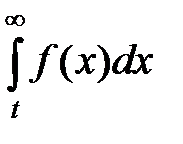 | λ(t) |
Вполне понятно, что у рассматриваемого типа объектов нет показателей восстанавливаемости.
Долговечность характеризуется следующими показателями:
g-процентный ресурс. Соответствует наработке, которая обеспечивается для изделия в обусловленной доле. Эта доля задается в процентах. Заданный процент соответствует вероятности того, что изделие обладает требуемой наработкой до отказа. Пример задания долговечности – 90%-й ресурс при наработке 10 000 часов. Величина g обычно устанавливается в диапазоне 90 – 98%;
назначенный ресурс. Это наработка, после которой эксплуатация прекращается независимо от технического состояния. Устанавливается для тех изделий, отказ которых приводит к тяжелым последствиям;
гарантийный срок службы (гарантированный ресурс). Календарное время, в течение которого изготовитель берет на себя обязанность в случае отказа из-за ненадежности устранить его своими силами и средствами.
Однако во многих случаях эти показатели играют справочную роль при выборе изделия для конкретного применения, так как обычно гарантийные обязательства изготовителя (поставщика) истекают ранее окончания гарантированного ресурса, да и у пользователя нет средств объективного измерения расхода ресурса. Например, гарантированный ресурс принтера 30 000 отпечатанных листов, который расходуется в течение нескольких лет, а срок гарантированного обслуживания составляет один год.
Для восстанавливаемых элементов вычислительных средств используют показатель:
Параметр потока отказов (W(t)) - отношение среднего числа отказов восстанавливаемого объекта за произвольно малую его наработку и значению этой наработки. Обозначим n(t) случайное число отказов за промежуток времени [o,t]. Тогда параметр потока отказов будет
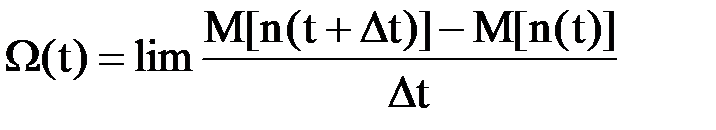 , (16)
, (16)
или
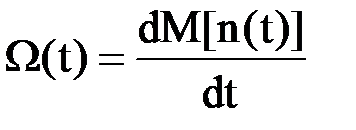 ,
,
где M[n(t)]-математическое ожидание числа отказов на интервал времени [o,t].
Параметр потока отказов обладает важным для практики свойством, состоящим в том, что во многих случаях
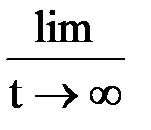
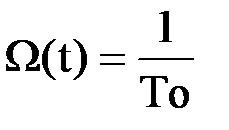 , (17)
, (17)
где T0 средняя наработка на отказ. Это свидетельствует о том, что с течением времени устанавливается стационарный процесс отказов и восстановлений, и среднее число отказов, происходящих в единицу времени, не зависит от продолжительности предыдущей эксплуатации.
В этих условиях для этапа нормальной эксплуатации объекта параметр потока отказов 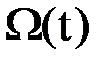 равен сумме интенсивностей отказов элементов (устройств), из которых состоят ВС, т.е.
равен сумме интенсивностей отказов элементов (устройств), из которых состоят ВС, т.е.
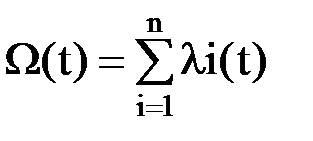 , (18)
, (18)
а значит, параметр потока отказов находится также, как интенсивность отказов элемента. Однако следует иметь в виду, что это не одно и то же, в общем случае эти характеристики не равны друг другу.
