Как решить систему дифференциальных уравнений?

Системы дифференциальных уравнений – традиционный «хедлайнер» темы диффуров, то есть, системы ДУ обычно изучаются в последнюю очередь. Всё начинается и всё заканчивается. Первый урок по теме назывался Дифференциальные уравнения первого порядка. Примеры решений, и вот настала пора заключительной статьи. Слава те Даже прослезился.

Предполагается, что читатель уже неплохо умеет решать дифференциальные уравнения, в частности, однородные уравнения второго порядка и неоднородные уравнения второго порядка с постоянными коэффициентами. В системах дифференциальных уравнений нет ничего сложного, и если вы уверенно расправляетесь с вышеуказанными типами уравнений, то освоение систем не составит особого труда.

Существуют два основных типа систем дифференциальных уравнений:

– Линейные однородные системы дифференциальных уравнений
– Линейные неоднородные системы дифференциальных уравнений

И два основных способа решения системы дифференциальных уравнений:

– Метод исключения.Суть метода состоит в том, что в ходе решения система ДУ сводится к одному дифференциальному уравнению.

– С помощью характеристического уравнения (так называемый метод Эйлера).

В подавляющем большинстве случаев систему дифференциальных уравнений требуется решить первым способом. Второй способ в условиях задач встречается значительно реже, за всю мою практику я решил им от силы 10-20 систем. Но и его тоже коротко рассмотрим в последнем параграфе данной статьи.

Сразу прошу прощения за теоретическую неполноту материала, но зато я включил в урок только те задания, которые реально могут встретиться на практике. То, что выпадает метеоритным дождем раз в пятилетку, вы вряд ли здесь найдете, и с такими нежданчиками следует обратиться к специализированным кирпичам по диффурам.

Линейные однородные системы дифференциальных уравнений

Простейшая однородная система дифференциальных уравнений имеет следующий вид:

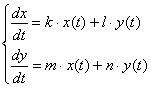
Собственно, почти все практические примеры такой системой и ограничиваются =)

Что тут есть?

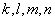– это числа (числовые коэффициенты). Самые обычные числа. В частности, один, несколько или даже все коэффициенты могут быть нулевыми. Но такие подарки подкидывают редко, поэтому числа 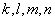чаще всего не равны нулю.

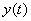и – это неизвестные функции. В качестве независимой переменной выступает переменная 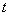– это «как бы икс в обычном дифференциальном уравнени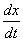и».

и 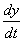– первые производные неизвестных функций и 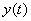соответственно.