Структура общего рещения ур-ия(1)
Понятие о дифференциальном уравнении.б)Общее и частное решения
а)Дифференциальным уравнением наз уравнение, связывающее искомую ф-цию одной или нескольких переменных, эти переменные и производные различных порядков донной ф-ии.
б)Общим решением дифференциального ур-ния g(x,y,y/,…,y(n))=0 n-го порядка наз такое его решение у=φ(х,с1,…,сп), кот явл ф-ией переменной х и произвольных независимых постоянных С1,С2,…,Сп. (независимость постоянных означает отсутствие каких-либо соотношений м/д ними). Частным решением дифференциального ур-ния наз решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных С1,С2,…,Сп.
Дифференциальные уравнения первого порядка с разделяющимися переменными.
ДУ 1-ого порядка с разделяющимися переменными назыв. Уравнения вида N(x)M(y) 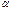 x +P(x)Q(y)dy=0 (1)
x +P(x)Q(y)dy=0 (1)
N(x),M(y),P(x),Q(y)-это функции, непрерывные на некотором промежутке.Ур-ие(1) разделим на произведение функции P(x)M(y).В результате получим 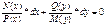 В этом случае говорят, что переменные разделены.Проинтегрирует последнее ур-ие:
В этом случае говорят, что переменные разделены.Проинтегрирует последнее ур-ие: 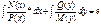 это и есть общий интеграл ур-ия(1)
это и есть общий интеграл ур-ия(1)
Линейные дифференциальные уравнения первого порядка.
Линейные ДУ 1-ого порядка назыв. Уравнение след. Вида y’+p(x)*y=f(x) (1), где p(x),f(x)-функции, непрерывные на некотором промежутке. Решение ур-ия(1) будем искать в виде y=u  (2) y’=u’
(2) y’=u’  +u
+u  ’ (3). Подставим y,y’ в ур-ие(1). В результате получим u’
’ (3). Подставим y,y’ в ур-ие(1). В результате получим u’ 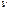 +u
+u 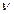 ’+p(x)u
’+p(x)u 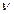 =f(x)
=f(x)
u’ 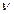 +u(
+u( 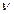 ’+p(x)
’+p(x) 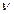 )=f(x) (4) функция
)=f(x) (4) функция 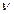 подбирается таким образом, чтобы выражения в скобках обратилось в 0, т.е. ф-я
подбирается таким образом, чтобы выражения в скобках обратилось в 0, т.е. ф-я 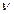 удовлетворит ур-ию
удовлетворит ур-ию 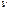 ’+p(x)
’+p(x) 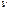 =0
=0
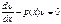
d 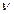 =-p(x)
=-p(x) 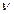 dx . Получили ур-ие с раздел переменными, разделим го на ф-ю
dx . Получили ур-ие с раздел переменными, разделим го на ф-ю 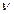 :
:
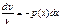 (5) Проинтегрируем ур-ие (5) ln
(5) Проинтегрируем ур-ие (5) ln 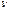 = -
= - 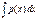
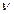 =e
=e 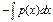 (что после е это степень) (6) Подставим найденное значение
(что после е это степень) (6) Подставим найденное значение 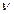 в ур-ие (4)
в ур-ие (4)
U’ e 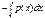 (что после е это степень)=f(x) По определению интеграла можно заменить
(что после е это степень)=f(x) По определению интеграла можно заменить 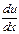 e
e 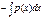 (что после е это степень)=f(x); du=f(x)e
(что после е это степень)=f(x); du=f(x)e 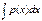 (что после е это степень)
(что после е это степень)
Интегрируем полученное ур-ие:u=f(x) e 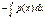 (что после е это степень)dx+c
(что после е это степень)dx+c
Подставим найденные ф-ии u и 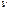 в равенство (2), получим y=(
в равенство (2), получим y=( 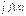 e
e 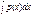 ( что после е это степень)dx+c) e
( что после е это степень)dx+c) e 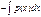 (что после е это степень).
(что после е это степень).
Дифференциальные уравнения второго порядка.
Рассмотрим ДУ 2-ого порядка F(x,y,y’,y’’)=0. Предположим, что его можно разрешить производной: y’’=F(x,y,y’) (1). Дано дифф. Ур-ие(1). Требуется найти решение ур-ия, удовлетворяющие условиям: y’= 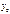 ’
’
y= 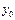 (2)
(2)
x=x 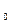
(x 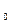 ,
, 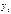 ,
, 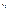 ’) кот. Назыв. Начальными данными.
’) кот. Назыв. Начальными данными.
Определение 1. Ф-я y= 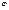 (x,C
(x,C 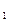 ,C
,C 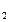 ) –назыв. Общим решением ур-ия(1), если для любых C
) –назыв. Общим решением ур-ия(1), если для любых C 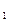 ,C
,C 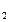 , взятых из некоторых промежутков, она явл. Решением ур-ия(1)
, взятых из некоторых промежутков, она явл. Решением ур-ия(1)
Определение 2. Те решения, кот. Получаются из общего решения фиксированием произвольных постоянных C 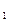 ,C
,C 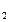 назыв. Частными.
назыв. Частными.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Линей. Однородными ДУ с постоян. коэфф-ами назыв. ур-ие вида: y’’+py’+qy=0 (1)
Pq –const
Структура общего рещения ур-ия(1)
Теорема 1. Если y 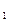 -явл. Решением ур-ия(1), то y=e y
-явл. Решением ур-ия(1), то y=e y 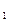 -также явл. Решением.
-также явл. Решением.
Теорема 2.Если y 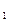 ,y
,y 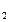 -это решения ур-ия(1), то y= y
-это решения ур-ия(1), то y= y 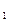 +y
+y 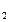 -это также решение ур-ия(1)
-это также решение ур-ия(1)
Опр-е 1. Функции y 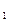 ,y
,y 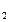 назыв. линейно независимыми, если их отношения не явл. Постоянными величинами. В противном случае ф-ии назыв. линейнонезависимыми.
назыв. линейно независимыми, если их отношения не явл. Постоянными величинами. В противном случае ф-ии назыв. линейнонезависимыми.
Теорема 3. Если y 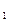 и y
и y 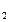 -это линейнонезависимые решения ур-ия (1), то функция y= c
-это линейнонезависимые решения ур-ия (1), то функция y= c 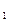 y
y 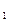 +c
+c 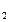 y
y 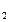 , где c
, где c 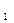 ,c
,c 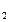 -соnst явл. общим решением ур-ия(1)
-соnst явл. общим решением ур-ия(1)
