Случайной величины в заданный интервал

Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу.

Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b:

Геометрически полученный результат можно истолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (а, b), равна площади криволинейной трапеции, ограниченной осью Ох, кривой распределения f(х) и прямыми х = а и х = b.

Нахождение функции распределения

По известной плотности распределения

Зная плотность распределения f(x), можно найти функцию распределения F(х) по формуле

.

Свойства плотности распределения

Свойство 1. Плотность распределения - неотрицательная функция:

f(x) > 0.

График плотности распределения называют кривой распределения.

Свойство 2. Несобственный интеграл от плотности распределения в пределах от -¥ до +¥ равен единице:

.

Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью Ох и кривой распределения, равна единице. В частности, если все возможные значения случайной величины принадлежат интервалу
(а, b), то

.

Закон равномерного распределения вероятностей

Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение:

Функция равномерного распределения:

Графики плотности и функции равномерного распределения изображены на рисунках.

Обозначается X~R(a,b).

Числовые характеристики непрерывных

Случайных величин

Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называют определенный интеграл:

(*)

Если возможные значения принадлежат всей оси Ох, то

.

Дисперсией НСВ называют математическое ожидание квадрата ее отклонения. Если возможные значения X принадлежат отрезку [a, b], то

,

если возможные значения принадлежат всей оси х, то

.

Среднее квадратическое отклонение НСВ определяется, как и для величины дискретной, равенством

.

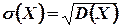Можно доказать, что свойства математического ожидания и дисперсии ДСВ сохраняются и для непрерывных величин.

Для вычисления дисперсии используют более удобные формулы:

,

.

Пример. Найти математическое ожидание н дисперсию НСВ X, распределенной равномерно в интервале (а, b).

Решение.

.

.

Замечание. Математическое ожидание и дисперсия случайной величины R, распределенной равномерно в интервале (0, 1), т. е. если а = 0, b = 1, как следует из примера, соответственно равны , .