Использование тригонометрических формул
Использование тригонометрических формул
Понижение степени подынтегральной функции (частный случай п.1)
Метод замены переменной
Универсальная тригонометрическая подстановка (частный случай п.3)
В рамках урока я постараюсь подробно разобрать все перечисленные методы и привести примеры решения типовых интегралов. Следует отметить, что данное разделение по параграфам весьма условно, поскольку очень часто вышеперечисленные правила используются одновременно.
Использование тригонометрических формул
Пример 1
Найти неопределенный интеграл.
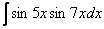
Сначала полное решение, потом комментарии.
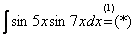
Используем формулу:
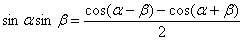

(1) Мы видим, что в подынтегральном выражении находится произведение двух функций. К сожалению, в интегральном исчислении нет удобной формулы для интегрирования произведения:  , поэтому приходится прибегать к различным ухищрениям. В данном случае мы прерываем решение значком
, поэтому приходится прибегать к различным ухищрениям. В данном случае мы прерываем решение значком 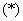 и поясняем, что используется тригонометрическая формула. Данная формула превращает произведение в сумму.
и поясняем, что используется тригонометрическая формула. Данная формула превращает произведение в сумму.
(2) Используем свойства линейности неопределенного интеграла – интеграл от суммы равен сумме интегралов; константу можно (и нужно) вынести за знак интеграла.
! Справка: При работе с тригонометрическими функциями следует помнить, что:
Косинус – это четная функция, то есть 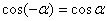 , минус исчезает без всяких последствий. В рассматриваемом примере:
, минус исчезает без всяких последствий. В рассматриваемом примере: 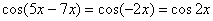
Синус – функция нечетная: 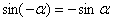 – здесь минус, наоборот – не пропадает, а выносится.
– здесь минус, наоборот – не пропадает, а выносится.
(3) Под интегралами у нас сложные функции (косинусы не просто от 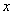 , а от сложного аргумента). Это простейшие из сложных функций, интегралы от них удобнее найти методом подведения под знак дифференциала. Более подробно с данным приёмом можно ознакомиться на уроке Метод замены переменной в неопределенном интеграле.
, а от сложного аргумента). Это простейшие из сложных функций, интегралы от них удобнее найти методом подведения под знак дифференциала. Более подробно с данным приёмом можно ознакомиться на уроке Метод замены переменной в неопределенном интеграле.
(4) Используем табличную формулу 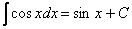 , единственное отличие, вместо «икса» у нас сложное выражение.
, единственное отличие, вместо «икса» у нас сложное выражение.
Готово.
Пример 2
Найти неопределенный интеграл.
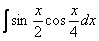
Это пример для самостоятельного решения, полное решение и ответ – в конце урока.
Пример 3
Найти неопределенный интеграл.
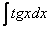
Классика жанра для тех, кто тонет на зачёте. Как Вы, наверное, заметили, в таблице интегралов нет интеграла от тангенса и котангенса, но, тем не менее, такие интегралы найти можно.
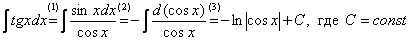
(1) Используем тригонометрическую формулу 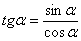
(2) Подводим функцию под знак дифференциала.
(3) Используем табличный интеграл 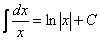 .
.
Пример 4
Найти неопределенный интеграл.
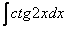
Это пример для самостоятельного решения, полное решение и ответ – в конце урока.
Пример 5
Найти неопределенный интеграл.
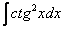
Степени у нас будут потихоньку повышаться =).
Сначала решение:
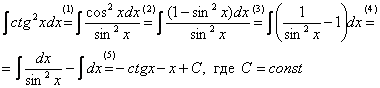
(1) Используем формулу 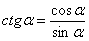
(2) Используем основное тригонометрическое тождество 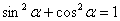 , из которого следует, что
, из которого следует, что 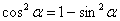 .
.
(3) Почленно делим числитель на знаменатель.
(4) Используем свойство линейности неопределенного интеграла.
(5) Интегрируем с помощью таблицы.
Пример 6
Найти неопределенный интеграл.
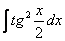
Это пример для самостоятельного решения, полное решение и ответ – в конце урока.
Также существуют интегралы от тангенсов и котангенсов, которые находятся в более высоких степенях. Интеграл от тангенса в кубе рассмотрен на уроке Как вычислить площадь плоской фигуры? Интегралы от тангенса (котангенса) в четвертой и пятой степенях можно раздобыть на странице Сложные интегралы.
