Корреляционно-регрессионный метод анализа связей

Тема. Статистическое изучение связи между явлениями.

Виды связей и методы их изучения.

Корреляционно-регрессионный метод анализа связей.

Определение параметров уравнения регрессии.

Измерение тесноты связи.

Виды связей и методы их изучения.

Изучение связей между явлениями в обществе и экономике производится при помощи специальных статистических методов. Они позволяют не только установить наличие или отсутствие связей между явлениями, но и придать им математическую определенность.

Явления экономической жизни могут состоять между собой в следующих видах связей:

1. Балансовая

2. Компонентная

3. Факторная.

Балансовая связь характеризует зависимость между источниками формирования и направлениями использования средств. Выражается формулой:

О_н + П = В + О_к (1)

О_н – остаток средств на начало периода;

П – поступление средств в течение периода;

В – выбытие средств в течение периода;

О_к – остаток средств на конец периода.

Компонентные связи характеризуются тем, что изменение статистического показателя определяется изменением компонентов, входящих в этот показатель как множители, Выражается формулой:

А = В * С (2)

Анализируются при помощи индексного анализа и его модификаций.

Факторная связь проявляется в согласованной вариации изучаемых показателей, одни их которых выступают как факторные, а другие – как результативные.

Факторные связи делятся на функциональные и корреляционные.

При функциональной связи изменение результативного фактора « у» полностью обусловлено воздействием факторного признака «х». Их связь выражается уравнением:

У = f (х) (3)

При корреляционной связи изменение результативного признака «у» не полностью зависит от изменения признака «х», так как на «у» могут воздействовать другие факторы, Поэтому значению фактора «х» могут соответствовать несколько значений результативного признака «у». Следовательно, их связь будет проявляться только в изменении средних величин результативного признака.

Корреляционные связи не являются жесткими ( полными) зависимостями и проявляются только в массе случаев.

Для анализа корреляционных связей используются методы корреляционно-регрессионного анализа.

Корреляционно-регрессионный метод анализа связей.

1.1.Определение параметров уравнения регрессии.

Существует два вида корреляции: парная и множественная.

Парнаярассматривает влияние вариации факторного признака «х» на результативный признак «у».

Множественная корреляция рассматривает влияние нескольких факторных признаков «х1», «х2» и т.д. на результативный признак «у».

При изучении связей показателей экономической деятельности применяются различные уравнения, называемые уравнениями регрессии. Они выражают изменение среднего уровня признака «у» в зависимости от изменения среднего уровня признака «х».

Уравнения регрессии устанавливают характер связи между признаками и могут быть линейными и криволинейными.

Линейная форма связи предполагает равномерное изменение результативного признака «у» под воздействием факторного признака «х». Уравнение регрессии имеет вид:

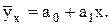(4.1)

Не все связи можно выразить линейным уравнением регрессии , часто применяются следующие уравнения:

- параболы второго порядка:

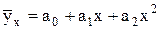, (4.2)

- параболы третьего порядка:

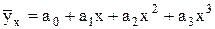, (4.3)

- показательной функции:

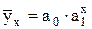, (4.4)

- полулогарифмической функции:

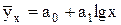, (4.5)

где 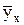- теоретические значения результативного признака;

а₀, а₁, а₂, а₃ - параметры уравнения регрессии;

х - эмпирические (реальные) значения факторного признака.

и т.д.

Поэтому, первый этап корреляционного анализа – выбор формы уравнения связи.

Второй этап корреляционного анализа – определение параметров уравнения.

Для определения параметров уравнения регрессии применяется метод наименьших квадратов:

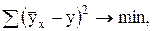(5)

Базируясь на методе наименьших квадратов, можно составить следующие системы нормальных уравнений для расчета параметров а₀, а₁ и т.д.:

а) для уравнения прямой

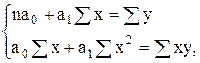(6.1)

б) для уравнения параболы второго порядка

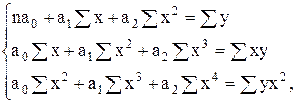(6.2)

в) для показательной функции

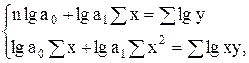(6.3)

г) для полулогарифмической функции

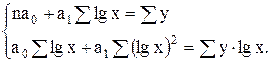(6.3)

Для определения параметров уравнений может использоваться либо способ совместного решения уравнений, либо способ определителей.

По способу определителей параметры уравнения прямой находятся следующим образом:

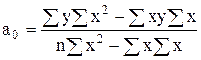
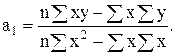(7.1)

Параметры уравнения показательной функции:

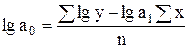
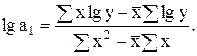(7.2)

Параметры уравнения полулогарифмической функции по методу определителей равны:

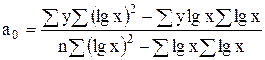
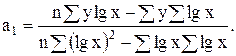(7.3)

Смысл параметров уравнения:

А₀ показывает значение признака у_х, не зависящее от значений «х».

А₁ называется коэффициентом регрессии и показывает, на сколько единиц в среднем изменится значение «у» при изменение «х» на единицу. А₁ может иметь знак (+) или (- ). При наличии знака минус между признаками «х» и «у» имеется обратная линейная связь.

1.2.Измерение тесноты связи.

Измерение тесноты связи – третий этап корреляционно-регрессионного анализа. Он предполагает определение степени влияния вариации признака «х» на вариацию признака «у».

Большинство методов измерения тесноты связи заключаются не в сопоставлении абсолютных значений «х» и «у», а их отклонений от средних, т.е. их вариации.

При наличии линейной связи для расчета тесноты связи используют коэффициент корреляции (коэффициент линейной корреляции):

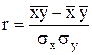
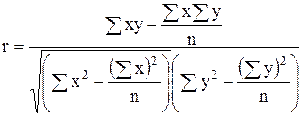(8)

Он может принимать значения от -1 до 1. При r = 1 - связь функциональная, прямая или обратная. Знак всегда должен совпадать со знаком коэффициента регрессии.

При наличии нелинейной зависимости между явлениями коэффициент регрессии не имеет смысла. В этом случае для определения тесноты связи используется индекс корреляции.

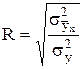(9), где

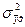- факторная дисперсия, обусловленная изменением результативного признака у только под воздействием изменения факторного признака х. Рассчитывается по формуле:

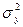- общая дисперсия результативного признака у, обусловленная воздействием всех факторов, а не только фактора х.

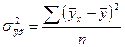
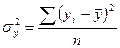(9.1), где

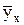- теоретические значения результативного признака, рассчитанные на основе уравнения регрессии;

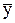- среднее значение результативного признака;

n - количество единиц в совокупности;

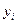- реальные значения результативного признака.

Индекс корреляции изменяется в пределах от 0 до 1. Если показатели тесноты связи будут равны 0, значит связь между х и у отсутствует.

Индекс корреляции является более точной мерой связи между явлениями, чем коэффициент корреляции.

Оценка силы связи производится на основании шкалы Чеддока и зависит от показателей тесноты связи.

Шкала Чеддока

Теснота связи	0,1-0,3	0,3-0,5	0,5-0,7	0,7-0,9	0,9-0,99
Сила связи	слабая	умеренная	заметная	высокая	весьма высокая

При проверке пригодности рассчитанного уравнения регрессии для практического использования применяют индекс детерминации, который равен отношению факторной и общей дисперсий.

Индекс детерминации показывает, какая часть в общей дисперсии признака приходится на долю факторной дисперсии, т.е. какая часть общей вариации признака «у» объясняется влиянием признака «х».

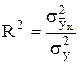. (10)

При работе с линейными моделями находится коэффициент детерминации путем возведения в квадрат коэффициента корреляции.

Индекс (коэффициент) детерминации используются для определения пригодности созданных моделей для практического применения. Модель пригодна для применения, если показатель тесноты связи превышает 0,7 (70%). В этом случае индекс детерминации превышает 50%,т.е. более половины вариации результативного признака объясняется влиянием факторного признака.

Оценка надежности параметров уравнений регрессии и показателей тесноты связи необходима, т.к. расчеты данных показателей проводятся, как правило, по выборочным данным, и могут быть расхождения между генеральными и выборочными характеристиками.

Точность коэффициента регрессии - параметра а₁ - оценивается по t-критерию:

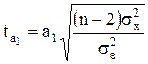. (7.23)

для оценки параметра а₀ используют формулу:

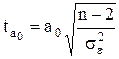, (7.24)

где а₁, а₀ - расчетные значения параметров;

n - количество пар значений признаков х и у;

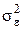- остаточная дисперсия, которая рассчитывается следующим образом:

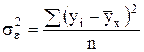. (7.25)

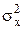- дисперсия факторного признака, рассчитываемая по формуле:

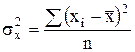. (7.26)

расчетные значения t-критериев сравнивают с табличными значениями для заданного уровня значимости α. Уровень значимости α показывает вероятность того, что рассчитанные показатели попадут в предельные интервалы.