П.1. Бинарная операция

Коми государственный педагогический институт

Кафедра алгебры, геометрии и

Теории и методики обучения математике

Методические рекомендации

По подготовке к государственному

Экзамену по математике

Сыктывкар, 2011

Составители: В.Ф.Бушуев, к.ф.-м.н., доцент;

Н.Г.Уляшова, к.ф.-м.н., доцент.

СОДЕРЖАНИЕ

ВОПРОС № 1. Определение группы. Свойства. Коммутативные (абелевы) группы. Конечные группы. Примеры групп. 3

ВОПРОС № 2. Определение кольца. Свойства. Коммутативные кольца. Делители нуля. Примеры колец. 9

ВОПРОС № 3. Определение поля. Свойства. Характеристика поля. Примеры полей. 12

ВОПРОС № 4. Определение векторного пространства. Свойства. Примеры векторных пространств. 16

ВОПРОС № 5. Конечномерные векторные пространства. Базис и размерность. Коорди-наты вектора. 20

ВОПРОС № 6. Евклидовы пространства. Ортонормированные базисы. 24

ВОПРОС № 7. Простые и составные числа. Основная теорема арифметики о разложе- нии чисел на простые множители и её применения. 28

ВОПРОС № 8. Приводимые и неприводимые многочлены. Теорема о разложении многочлена на неприводимые множители над произвольным полем. 32

ВОПРОС № 9. Разложение многочлена на неприводимые множители над полем комплексных и над полем действительных чисел. 36

ВОПРОС № 10. Корни многочлена. Отыскание целых и рациональных корней много- члена с целыми коэффициентами. 39

ВОПРОС № 11. Теорема о делении с остатком для целых чисел и для многочленов. 43

ВОПРОС № 12. Алгоритм Евклида для целых чисел и для многочленов. НОД и НОК. 47

ВОПРОС № 1 Определение группы. Свойства. Коммутативные (абелевы) группы. Конечные группы. Примеры групп.

Дадим определения понятий, на которых основано понятие группы, а именно понятие бинарной операции, нейтрального элемента относительно этой операции и элемента, симметричного данному элементу.

п.1. Бинарная операция.

Опр.1. Пусть А - произвольное непустое множество, - декартов квадрат множества А (т.е. множество всех пар элементов множества А). Бинарной операцией на множестве А называется отображение , которое каждой паре 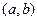элементов множества А ставит в соответствие единственный элемент , обозначаемый .

Элемент с называют композицией элементов а и b (или результатом операции *, примененной к элементам а и b).

Часто используются аддитивная и мультипликативная форма записи бинарной операции.

При аддитивной форме записи бинарную операцию * называют сложением и обозначают +. При этом вместо пишут и элемент называют суммой элементов а и b.

При мультипликативной форме записи бинарную операцию * называют умножением и обозначают ∙. При этом вместо пишут и элемент называют произведением элементов а и b.