Показатели эффективности инвестиционных проектов

Дисконтирование по простым и сложным процентам

Определение. Величина S(t₀) называется современным, приведенным или текущим значением будущей суммы S(t₀+Т) в настоящий момент t₀, которая при инвестировании в начальный момент t₀ по ставке i(t₀) процента даст через время Т требуемое наращенное значение S(t₀+Т), при этом она может быть выражена следующим образом

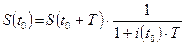, в случае, если 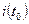– простая ставка процента, и

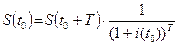, в случае, если 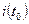– сложная ставка процента.

Операция вычисления современной стоимости будущей суммы денег называется математическим дисконтированием, величина 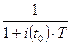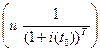дисконтным множителем, разность 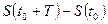дисконтом суммы S(t₀+T) и обозначается через D.

Пример. Кредит выдан на 6 месяцев под 80% годовых с условием вернуть 3000 руб. Какую сумму получил заемщик в момент заключения договора и чему равен дисконт?

Предположим, что T = 360 дней, следовательно 6 месяцев = 180 дней. Тогда

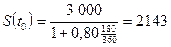руб. Дисконт составит D=857 руб.

Определение. Величина 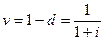- называется эффективной ставкой дисконта, где d – годовая учетная ставка.

При заданных S(Т) , 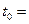0 и сложной годовой процентной ставке i мы получим следующую формулу дисконтирования:

,

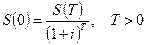а при годовой номинальной ставке :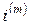

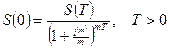
Сложная годовая учетная ставка

Определение. Если годовая учетная ставка d эквивалентна годовой ставке i сложных процентов, то d будем называть сложной годовой учетной ставкой.

Из равенства 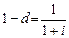следует, что 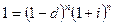. Теперь, используя равенства 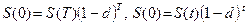, мы получим: 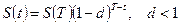при сложной учетной ставке, где 0<t<T.

Аналогично получается

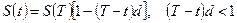при простой учетной ставке.

Следовательно, дисконтный множитель выглядит так:

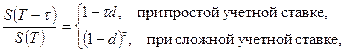
здесь 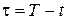время до платежа.

ИЗМЕРЕНИЕ ЭФФЕКТИВНОСТИ ИНВЕСТИЦИЙ.

АНАЛИЗ РИСКОВ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ

Управление инвестиционными процессами, связанными с вложениями денежных средств в долгосрочные материальные и финансовые активы, представляет собой наиболее важный и сложный раздел финансовой математики.

Показатели эффективности инвестиционных проектов

Основными показателями эффективности инвестиционных проектов являются: чистая современная стоимость, индекс рентабельности, внутренняя норма доходности и срок окупаемости.

Чистая современная стоимость.Основная идея чистой современной стоимости (NPV) заключается в том, чтобы найти разницу между инвестиционными затратами и будущими доходами, выраженную в скорректированной во времени денежной величине. Пусть I₀ – сумма первоначальных затрат, т.е. сумма инвестиций на начало проекта; PV – современная стоимость денежного потока на протяжении экономической жизни проекта. Тогда

,

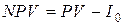где, как известно,

,

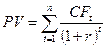здесь r – норма дисконта; n - число периодов реализации проекта; CF_t - чистый поток платежей в периоде t. Отсюда,

.

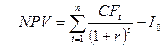Если NPV >0 – это означает, что в течение своей экономической жизни проект возместит первоначальные затраты I₀, обеспечит получение прибыли согласно заданному стандарту r, а также ее некоторый резерв, равный NPV. Если NPV <0 – это показывает, что заданная норма прибыли не обеспечивается и проект убыточен. Если NPV = 0 - проект только окупает производственные затраты, но не приносит дохода.

Пример. Фирма собирается вложить средства в приобретение нового оборудования, стоимость которого вместе с доставкой и установкой составит 100.000 руб. Ожидается, что внедрение оборудования обеспечит получение на протяжении 6 лет чистых доходов в 25.000, 30.000, 35.000, 40.000, 45.000 и 50.000 руб. соответственно. Норма дисконта 10%. Определить экономическую эффективность проекта.

По формуле (проверьте самостоятельно) NPV =57302,37 – остаток полученный от проекта, после расчетов с кредиторами.

Индекс рентабельности проекта (PI).Сначала рассмотрим пример.

Пример. Предположим, что имеется два проекта. Норма дисконта 10%. Оценка денежных потоков и расчет NPV приведены в таблице:

Проект	I0	CFt	PV	NPV
X	-10.000	16.500	15.000	5.000
Y	-100.000	115.000	105.000	5.000

Чистая современная стоимость обоих проектов оставляет 5.000 руб.и (в случае необходимости) сложно выбрать лучший проект. Поэтому используются другие показатели.

Индекс рентабельности (PI) – показывает, сколько единиц современной величины денежного потока приходится на единицу предполагаемых первоначальных затрат, т.е.

.

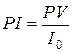Если PI >1, то современная стоимость денежного потока превышает первоначальные инвестиции, обеспечивая тем самым наличие положительной величины NPV. При PI=1 величина NPV <0 и инвестиции не приносят дохода. Если PI <1, проект не обеспечивает заданного уровня рентабельности. Следовательно, проект принимается, если PI >1. Для рассматриваемого примера:

; .

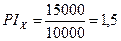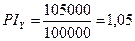Следует отдать предпочтение проекту Х.

Внутренняя норма доходности (IRR). Под внутренней нормой доходности понимают процентную ставку, при которой чистая современная стоимость инвестиционного проекта равна нулю. Внутренняя норма доходности определяется решением уравнения:

.

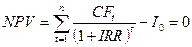Это уравнение решается итерационным методом.

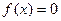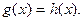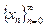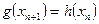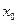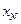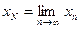Замечание.Нелинейное уравнение эквивалентными преобразованиями приводится к виду: Предположим, что x скалярный аргумент. Построение сходящейся последовательности по правилу при заданном называется итерационным методом вычисления корня , где . Из наиболее известных итерационных методов приведем два: метод Ньютона и метод секущих.

Метод Ньютона. Здесь в качестве 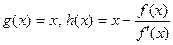. Итерационная формула задается так:

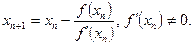
Метод секущих. Здесь итерационная формула выглядит так:

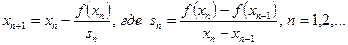
и 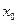, 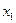- два заданных числа такие, что .

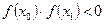Практическое применение итерационных методов осложнено, если нет специализированного финансового калькулятора. В этом случае применяется метод последовательных итераций с использованием табулированных значений дисконтирующих множителей. Для этого с помощью таблиц выбираются два значения коэффициента дисконтирования 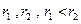таким образом, чтобы в интервале 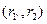функция NPV = f(r) меняла свой знак с «+» на «-» или с «-» на «+». Далее применяют формулу:

.

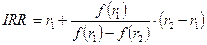Точность вычислений обратно пропорциональна длине интервала 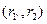, а наилучшая аппроксимация с использованием табулированных значений достигается в случае, когда длина интервала минимальна (равна 1%), т.е. 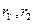- ближайшие друг к другу значения коэффициента дисконтирования, удовлетворяющие условиям (в случае изменения знака функции с «+» на «-»: 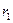- значение табулированного коэффициента дисконтирования, минимизирующее положительное значение показателя NPV, т.е. 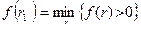; 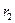- значение табулированного коэффициента дисконтирования, максимизирующее положительное значение показателя NPV, т.е. 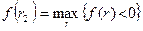. Путем взаимной замены коэффициентов 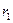и 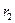аналогичные условия выписываются для ситуации, когда функция меняет знак с «-» на «+»).

Если NPV =0 современная стоимость проекта PV равна по абсолютной величине I₀, следовательно, они окупаются. В общем случае, чем выше IRR, тем больше эффективность инвестиций. На практике IRR сравнивается с r (нормой дисконта). При этом: если IRR>r, то проект обеспечивает положительную NPV и доходность, равную IRR-r. Если IRR<r, затраты превышают доходы, и проект убыточен. Таким образом, проект принимается, если IRR>r.

Пример. Определить значение IRR для проекта, рассчитанного на три года, требующего инвестиций в размере 10 млн.руб. и имеющего предполагаемые денежные поступления в размере 3 млн.руб.; 4 млн.руб., 7 млн.руб.

Возьмем два произвольных значения коэффициента дисконтирования: 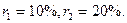Приведем соответствующие расчеты с использованием этих значений:

Год	Поток	Расчет 1 r = 10%	Расчет 2 r = 20%
t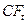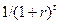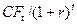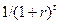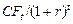
0-й	-10	1,000	-10,00	1,000	-10,00
1-й		0,909	2,73	0,833	2,50
2-й		0,826	3,30	0,694	2,78
3-й		0,751	5,26	0,579	4,05
		NPV = 1,29	NPV = -0,67

Используя расчеты 1 и 2 мы находим значение IRR следующим образом:

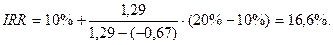
Полученное значение можно уточнить. Допустим, что путем нескольких итераций мы определили ближайшие целые значения коэффициента дисконтирования, при которых NPV меняет знак: при r =16% NPV = 0,05 и при r =17% NPV = -0,14

Год	Поток	Расчет 3 r = 16%	Расчет 4 r = 17%
t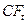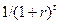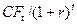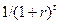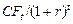
0-й	-10	1,000	-10,00	1,000	-10,00
1-й		0,862	2,59	0,855	2,57
2-й		0,743	2,97	0,731	2,92
3-й		0,641	4,49	0,624	4,37
		NPV = 0,05	NPV = -0,14

Тогда уточненное значение IRR будет равно:

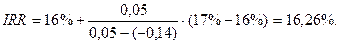
Срок окупаемости (PP).Алгоритм расчета срока окупаемости зависит от равномерности распределения прогнозируемых доходов от инвестиции. Если доход распределен по годам равномерно, то срок окупаемости рассчитывается делением единовременных затрат на величину годового дохода, обусловленного ими. При получения дробного числа оно округляется в сторону увеличения до ближайшего целого. Если прибыль распределена неравномерно, то срок окупаемости рассчитывается прямым подсчетом числа лет, в течение которых инвестиция будет погашена кумулятивным доходом. Общая формула расчета PP выглядит так:

.
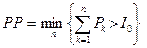