Прямые методы для систем с разреженными матрицами

Во многих приложениях приходится решать систему

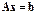
с разреженной матрицей A. Назовем –матрицу A разреженной, если число ее ненулевых элементов .

При решении таких систем естественно хранить в памяти ЭВМ только ненулевые элементы. Можно надеяться, что в случае разреженных матриц как вычислительная работа, так и требуемый объем памяти значительно сократятся. Проблема состоит в том, что на этапе исключения неизвестных в методе Гаусса либо на этапе построения L и U матриц в компактной схеме Гаусса могут возникать

Рис. 3.3. LU-факторизация диагональной матрицы со строчным

и столбцовым окаймлением

новые ненулевые элементы. Обратимся к следующему простому при-меру (рис. 3.3). Хотя исходная матрица A здесь имеет ничтожное число ненулевых членов, матрицы L и U имеют такую же структуру

Рис. 3.4. LU-факторизация преобразованной диагональной матрицы

со строчным и столбцовым окаймлением

ненулевых элементов, как и для полностью заполненной матрицы. В

то же время перестановкой строк и столбцов систему можно преоб-разовать к виду, который сохраняет свойство разреженности исходной матрицы в матрицах разложения (рис. 3.4). В общем случае, конечно, не всегда удается полностью сохранить разреженность. Поэтому перестановки строк и столбцов выбирают такими, чтобы заполняемость матрицы в процессе исключения переменных была минимальной.

На языке матричного описания эта задача выглядит следующим образом. Пусть P и Q – -матрицы перестановок строк и столбцов, причем . Матрицы P и Q легко получить из единичной матрицы, в которой переставлены соответствующие строки (столбцы). Например, матрица перестановки первой и третьей строк -матрицы приведена на рис. 3.5.

Преобразуем систему линейных алге-браических уравнений следующим образом:

или

где – переупорядоченная форма A, , . К системе будем применять прямой метод решения (его эффективность зависит от выбора матриц P и Q) и далее найдем , так как . Задача осложняется тем, что перестановка строк и столбцов определяющим образом влияет не только на разреженность матриц разложения, но и на численную устойчивость прямого метода.

Симметричные матрицы. Если матрица A линейной системы является симметрической положительно определенной, то процесс исключения переменных по схеме Холесского является численно устойчивым при любом выборе главных элементов из числа диагональных членов. Таким образом, если положить , т. е. при перестановке k–й и j–й строк осуществлять перестановку k–го и j–го столбцов, то выбор матрицы P можно производить только исходя из требования минимизации заполнения матрицы .

Задача численного решения линейной системы сводится в этом случае к выполнению трех последовательных шагов:

Шаг 1. Формирование матрицы и вектора .

Шаг 2. Решение упорядоченной системы .

Шаг 3. Вычисление вектора .

Рассмотрим более подробно, как реализуется Шаг 1. Вообще говоря, для -матрицы A существует различных упоря-дочиваний, из которых одно или более оказывается оптимальным в смысле заполнения. Задача отыскания оптимальных упорядочиваний является чрезвычайно трудной и практически нерешенной на сегодняшний день. Существующие процедуры реализации шага 1 являются эвристическими. Они обеспечивают понижение заполнения матрицы , однако не гарантируют достижение точного минимума. Опишем в общих чертах одну из таких процедур – алгоритм минимальной степени.

Основная идея алгоритма минимальной степени заключается в локальной минимизации заполнения за счет выбора главного элемента в той строке и столбце, которые обеспечивают внесение наименьшего числа ненулевых элементов в множитель . Рассмотрим, например, k–й шаг исключения прямого хода Гаусса. В поддиагональных позициях столбцов с 1–го по (k-1)–й расположены нулевые элементы. Для исключения переменной xk на этом шаге k–я строка, нормированная соответствующим образом, вычитается из всех тех строк, которые имеют ненулевые элементы в k–м столбце. Следовательно, чтобы минимизировать число новых ненулевых элементов, достаточно просмотреть активную подматрицу матрицы Ak-1, выбрать строку с наименьшим числом ненулевых элементов, назовем ее l–й строкой, и переставить как строки, так и столбцы с номерами l, k. После такой перестановки в матрицу Ak-1 вносятся новые ненулевые элементы, т. е. формируется портрет матрицы Ak , и процесс имитации исключения переменных продолжается. Выполнив имитацию (n-1)–го шага исключения, построим в итоге из единичной матрицы I искомую матрицу перестановок P.

Матрицы общего вида. На k–м шаге алгоритма Гаусса при решении линейных систем с разреженной матрицей A произвольной структуры необходимо выбирать в качестве главного элемента такой элемент , который прежде всего обеспечивает устойчивость вычислительного процесса и в то же время по возможности минимизирует заполняемость матрицы Ak. Это достигается введением специального барьера – числа u≥1 и выделением множества элементов из активной подматрицы матрицы Ak-1, которые удовлетворяют условию

,

где – элемент множества Sk-1.

Для каждого из таких элементов вводится числовая оценка

,

где r(l,k) – число ненулевых элементов в l–й строке активной части матрицы Ak-1, c(m,k) – число ненулевых элементов в m–м столбце этой же части матрицы Ak-1. В качестве главного элемента на k–м шаге прямого хода Гаусса выбирается такой элемент

,

для которого

.

Лекция 4

ИТЕРАЦИОННЫЕ МЕТОДЫ

ЦЕЛЬ ЛЕКЦИИ: Дать общую схему линейных итерационных методов первого порядка и построить на её основе методы простой итерации, Гаусса–Зейделя, последовательной релаксации; сравнить эти методы по вычислительным затратам на итерации.

В случае больших разреженных СЛАУ предпочтение отдаётся итерационным методам, т. к. они, во-первых, не приводят к появлению на итерациях новых ненулевых элементов, во-вторых, оказываются более эффективными по затратам машинного времени.