Задание № 6. Найти общее решение дифференциального уравнения, удовлетворяющее начальным условиям, и частное решение

.

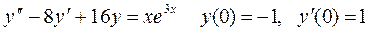Задание № 7. Разложить на отрезке 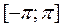в ряд Фурье и построить график суммы ряда для функции: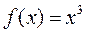

ВАРИАНТ №8

Задание № 1. Исследовать несобственный интеграл на сходимость

Задание № 2. Вычислить сумму ряда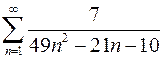

Задание № 3. Исследовать ряды на сходимость

1. 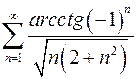2.

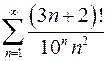
Задание № 4. Найти область сходимости степенного ряда: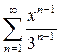

Задание № 5. Решить дифференциальное уравнение:

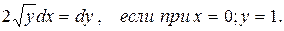
Задание № 6. Найти общее решение дифференциального уравнения, удовлетворяющее начальным условиям, и частное решение

.

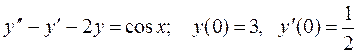Задание № 7. Разложить на отрезке 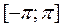в ряд Фурье и построить график суммы ряда для функции: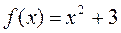

ВАРИАНТ №9

Задание № 1. Исследовать несобственный интеграл на сходимость

Задание № 2. Вычислить сумму ряда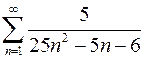

Задание № 3. Исследовать ряды на сходимость

1. 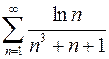2.

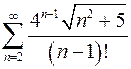
Задание № 4. Найти область сходимости степенного ряда: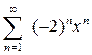

Задание № 5. Решить дифференциальное уравнение:

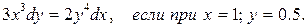
Задание № 6. Найти общее решение дифференциального уравнения, удовлетворяющее начальным условиям, и частное решение

.

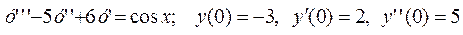Задание № 7. Разложить на отрезке 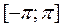в ряд Фурье и построить график суммы ряда для функции: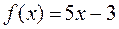

ВАРИАНТ №10

Задание № 1. Исследовать несобственный интеграл на сходимость

Задание № 2. Вычислить сумму ряда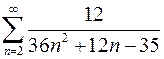

Задание № 3. Исследовать ряды на сходимость

1. 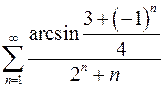2.

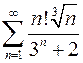
Задание № 4. Найти область сходимости степенного ряда: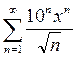

Задание № 5. Решить дифференциальное уравнение:

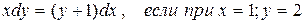
Задание № 6. Найти общее решение дифференциального уравнения, удовлетворяющее начальным условиям, и частное решение

.

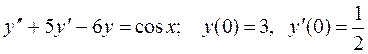Задание № 7. Разложить на отрезке 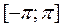в ряд Фурье и построить график суммы ряда для функции: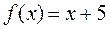

РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ

Основная литература:

1. Белова, Т.И. Вычисление неопределенных интегралов. Обыкновенные дифференциальные уравнения. Компьютерный курс: учеб. пособие / Т.И.Белова, А.А.Грешилов, И.В.Дубограй; Ред. А.А.Грешилов. - М.: Логос, 2004. - 184 с. + 1 эл. опт. диск (CD-ROM).

2. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. - 22-е изд., перераб. - СПб.: Профессия, 2006. - 432 с.

3. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. - 22-е изд., перераб. - СПб.: Профессия, 2005. - 432 с.

4. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. для вузов. В 2 ч. Ч.1 / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий. - 4-е изд., стереотип. - М.: Дрофа, 2004. - 725 с.

5. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч. 1. Дифференциальное и интегральное исчисление / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; Ред. В.А.Садовничий. - 3-е изд., испр. - М.: ДРОФА, 2001. - 725 с.

6. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч.2. Ряды, несобственные интегралы, ряды Фурье, преобразование Фурье / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; ред. В.А.Садовничий . - 3-е изд., испр. - М.: ДРОФА, 2001. - 712 с.

7. Голоскоков, Д.П. Уравнения математической физики. Решение задач в системе Maple: учеб. для вузов / Д.П.Голоскоков. - СПб.: Питер, 2004. - 538с.

8. Гурова, З.И. Высшая математика. Начальный курс с примерами и задачами: учеб. для втузов / З.И.Гурова, С.Н.Каролинская, А.П.Осипова; Ред. А.И.Кибзун. - М.: Физматлит, 2002. - 351 с.

9. Лукьянов, А.В. Обыкновенные дифференциальные уравнения: учеб. пособие по решению задач / А.В.Лукьянов, Ю.Д.Погуляев. - Челябинск: Полиграф-Мастер, 2006.

10. Мартинсон, Л.К. Дифференциальные уравнения математической физики: учеб. для втузов / Л.К.Мартинсон, Ю.И.Малов; Ред. В.С. Зарубин, А.П.Крищенко. - 2-е изд. - М.: МГТУ им. Н.Э. Баумана, 2002. - 367 с.

11. Высшая математика в вопросах и задачах: учеб. пособие для вузов / В.Ф.Бутузов, Н.Ч.Крутицкая, Г.Н.Медведев, А.А.Шишкин; Ред. В.Ф.Бутузов . - 5-е изд., испр. - М.: ФИЗМАТЛИТ, 2002. - 479 с.

12. Пантелеев, А.В. Теория функций комплексного переменного и операционное исчисление в примерах и задачах : учеб. пособие для втузов / А.В.Пантелеев, Якимова А.С. - М. : Высш. шк., 2001. - 446 с.

13. Пискунов, Н.С. Дифференциальное и интегральное исчисления: учеб. для втузов. В 2 т. Т. 1 / Н.С.Пискунов. - Стер. изд. - М. : ИНТЕГРАЛ-ПРЕСС, 2004. - 415 с.

14. Пискунов, Н.С. Дифференциальное и интегральное исчисления: учебник для втузов. В 2 т. Т. 2 / Н.С.Пискунов. - Стер. изд. - М.: ИНТЕГРАЛ-ПРЕСС, 2004. - 544 с.

15. Полянин, А.Д. Методы решения нелинейных уравнений математической физики и механики: учеб. пособие для вузов / А.Д.Полянин, В.Ф.Зайцев, А.И.Журов. - М.: Физматлит, 2005. - 254 с.

16. Русак, В.Н. Математическая физика: учеб. пособие для ун-тов / В.Н.Русак. - 2-е изд., испр. - М.: Едиториал УРСС, 2006. - 244 с.

17. Шипачев, В.С. Высшая математика: учеб. пособие для вузов / В.С.Шипачев. - М.: Высш. шк., 2002. - 176 с.

Дополнительная литература:

1. Антоневич, А.Б. Задачи и упражнения по функциональному анализу. Учеб.пособие. / А.Б.Антоневич, П.Н.Князев, Я.В.Радыно – М.: Едиториал УРСС, 2004 – 205с.

2. Босс, В. Лекции по математике: анализ. / В.Босс – М.: Едиториал УРСС, 2004 – 213с.

3. Босс, В. Лекции по математике: дифференциальные уравнения. / В.Босс– М.: Едиториал УРСС, 2004 – 204 с.

4. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2 / П.Е.Данко [и др.]. - 7-е изд., испр. - М.: Оникс: Мир и Образование(М.), 2008. - 448 с.

5. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2 / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова, С.П.Данко. - 6-е изд. - М.: Оникс: Мир и Образование(М.), 2007. - 416 с.

6. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2-х ч. Ч.2 / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. - 6-е изд. - М.: Оникс: Мир и Образование(М.), 2005. - 416 с.

7. Задачи и упражнения по математическому анализу для втузов / Ред. Б.П.Демидович. – М.: АСТ-Астрель, 2004. - 495 с.

8. Зайцев, В.Ф. Справочник по обыкновенным дифференциальным уравнениям / В.Ф.Зайцев, А.Д.Полянин. - М.: Физматлит, 2001. - 576 с.

9. Кудрявцев, Л.Д. Краткий курс математического анализа: учеб. для вузов. В 2 т. Т. 1 Дифференциальное и интегральное исчисления функции одной переменной. Ряды / Л.Д.Кудрявцев. - 2-е изд., перераб. и доп. - Висагинас: Alfa, 1998. - 397 с.

10. Лукьянов, А.В. Введение в теорию уравнений с частными производными и математическую физику: метод. указания по решению уравнений теплопроводности / А.В.Лукьянов, Ю.Д.Погуляев. - Челябинск: Полиграф-Мастер, 2006. - 59 с.

11. Подчуфаров, Ю.Б. Физико-математическое моделирование систем управления и комплексов / Ю.Б.Подчуфаров; Ред. А.Г. Шипунов. - М.: Физматлит, 2002. - 167 с.

12. Привалов, И.И. Введение в теорию функций комплексного переменного: учеб. для вузов / И.И. Привалов - 14-е изд., стереотип. - М.: Высш. шк., 1999. - 432с.

13. Сборник задач и упражнений по математическому анализу. Ч.1 / С.И.Ляшко [и др.]; Ред. И.И. Ляшко. - М.; СПб.; Киев: Диалектика, 2001. - 430 с.

14. Сикорский, Ю.С. Обыкновенные дифференциальные уравнения. С приложением их к некоторым техническим задачам / Ю.С.Сикорский; Ред. С.Г. Михлин. - 2-е изд., стереотип. - М.: УРСС, 2005. - 155 с.

15. Стакун, А.А. Высшая математика: конспект лекций с решениями типовых примеров и метод. указ. к инд. заданиям (для студ.-заоч.). В 2 ч. Ч.2 / А.А.Стакун, С.И.Фролов. - СПб.: Политехника, 2001. - 147 с.

16. Цлаф, Л.Я. Вариационное исчисление и интегральные уравнения: справ. рук. / Л.Я.Цлаф. - 3-е изд., стереотип. – М.: Лань, 2005. - 191 с.