Теорема. (Необходимые условия экстремума)
Если функция f(x,y) в точке (х0, у0) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю 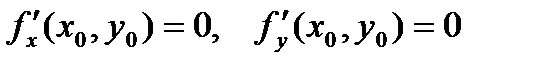 , либо хотя бы одна из них не существует. Эту точку (х0, у0) будем называть критической точкой.
, либо хотя бы одна из них не существует. Эту точку (х0, у0) будем называть критической точкой.
Теорема. (Достаточные условия экстремума).
Пусть в окрестности критической точки (х0, у0) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:
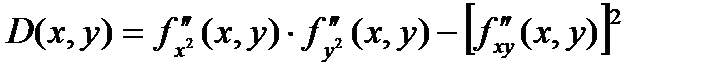
1) Если D(x0, y0) > 0, то в точке (х0, у0) функция f(x, y) имеет экстремум, если
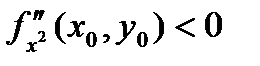 - максимум, если
- максимум, если 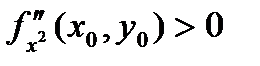 - минимум.
- минимум.
2) Если D(x0, y0) < 0, то в точке (х0, у0) функция f(x, y) не имеет экстремума
В случае, если D = 0, вывод о наличии экстремума сделать нельзя.
Условный экстремум ФНП
Условный экстремум находится, когда переменные х и у, входящие в функцию u = f( x, y), не являются независимыми, т.е. существует некоторое соотношение
j(х, у) = 0, которое называется уравнением связи.
Тогда из переменных х и у только одна будет независимой, т.к. другая может быть выражена через нее из уравнения связи.
Тогда u = f(x, y(x)). 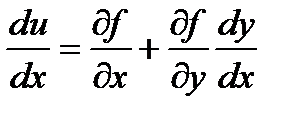
В точках экстремума: 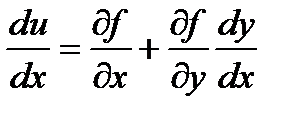 =0 (1)
=0 (1)
Кроме того: 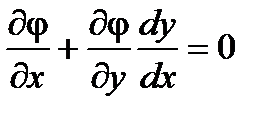 (2)
(2)
Умножим равенство (2) на число l и сложим с равенством (1).
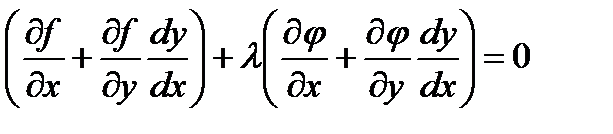
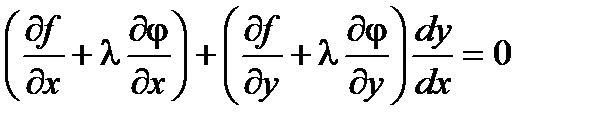
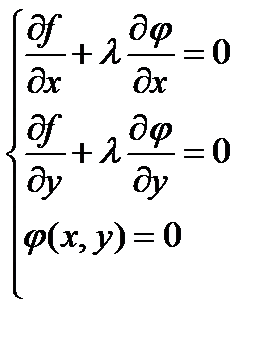 Для выполнения этого условия во всех точках найдем неопределенный коэффициент l так, чтобы выполнялась система трех уравнений:
Для выполнения этого условия во всех точках найдем неопределенный коэффициент l так, чтобы выполнялась система трех уравнений:
Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум.
Выражение u = f(x, y) + lj(x, y) называется функцией Лагранжа.
Основные понятия теории дифферинциальных уравнений.
Определение. Дифференциальным уравнениемназывается уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.
Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.
Определение. Общим решениемдифференциального уравнения называется такая дифференцируемая функция y = j(x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.
Свойства общего решения.
1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.
2) При каких- либо начальных условиях х = х0, у(х0) = у0 существует такое значение С = С0, при котором решением дифференциального уравнения является функция у = j(х, С0).
Определение. Решение вида у = j(х, С0) называется частным решениемдифференциального уравнения.
27Определение. Задачей Кошиназывается нахождение любого частного решения дифференциального уравнения вида у = j(х, С0), удовлетворяющего начальным условиям у(х0) = у0.
28-29.ДУ первого порядка. с разделяющимися переменными
