Температурное поле МТИ в полубесконечном теле
При действии мгновенного точечного источника (МТИ) на поверхность полу бесконечного тела, температурное поле имеет центральную симметрию, и для его описания используются сферические координаты. Изотермические поверхности представляют собой полусферы. Граничную поверхность тела будем считать адиабатической. Пусть МТИ действует в начале координат, ось 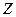 направлена внутрь тела. Для того чтобы воспользоваться формулой определения температурного поля для бесконечного тела, количество тепла, внесенное в тело в этой точке, как отмечалось, необходимо удвоить.
направлена внутрь тела. Для того чтобы воспользоваться формулой определения температурного поля для бесконечного тела, количество тепла, внесенное в тело в этой точке, как отмечалось, необходимо удвоить.
Теплоотдачей с поверхности 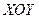 можно пренебречь, так как распределение теплоты в полу бесконечном теле в основном зависит от распространения ее вглубь тела за счет теплопроводности. Распределение температуры в точках полу бесконечного тела при действии МТИ описывается следующим выражением:
можно пренебречь, так как распределение теплоты в полу бесконечном теле в основном зависит от распространения ее вглубь тела за счет теплопроводности. Распределение температуры в точках полу бесконечного тела при действии МТИ описывается следующим выражением:
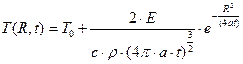 (1)
(1)
Где:
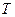 - температура от действия источника в точке, на расстоянии
- температура от действия источника в точке, на расстоянии 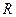 от места введения теплоты через время
от места введения теплоты через время 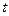 после его действия;
после его действия;
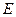 - количество введенной теплоты, Дж;
- количество введенной теплоты, Дж;
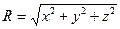 - расстояние от рассматриваемой точки до начала координат, где была введена теплота, см;
- расстояние от рассматриваемой точки до начала координат, где была введена теплота, см;
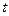 - время, прошедшее с момента введения теплоты;
- время, прошедшее с момента введения теплоты;
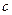 - теплоёмкость,
- теплоёмкость, 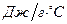 ;
;
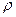 - плотность;
- плотность;
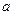 - коэффициент температуропроводности.
- коэффициент температуропроводности.
Выражение (1) является решением уравнения (5) введения для полубесконечного тела.
Исследуем структуру температурного поля МТИ. Положим в (1) 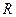 =0. Температура в центре изменяется по гиперболическому закону.
=0. Температура в центре изменяется по гиперболическому закону.
Выведем формулу, определяющую время достижения заданной температуры в центре источника.
Решение: Положим 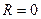 , из (1), разрешая относительно времени
, из (1), разрешая относительно времени 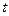 , получим:
, получим:

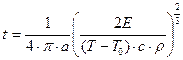 (2);
(2);
Определить самостоятельно с помощью системы MATLAB, при каких значениях времени 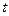 температура
температура 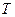 в центре источника снизится до значений равных:
в центре источника снизится до значений равных:
а) температуре кипения,
б) температуре плавления,
в) температуре 1000 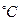 ,
,
для материалов: 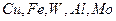 при значении
при значении 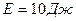 .
.
Для этого положить 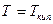 для заданного материала и провести вычисления. Выполнить тоже для
для заданного материала и провести вычисления. Выполнить тоже для 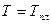 и
и 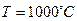 , результаты свести в таблицу и объяснить.
, результаты свести в таблицу и объяснить.
Исследуем зависимость распределения температуры в материале от расстояния 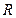
до точки воздействия МТИ при некотором фиксированном моменте времени.
Для этого с помощью системы MATLAB представим графически распределения температуры 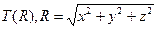 , при значении
, при значении 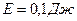 , для момента времени
, для момента времени 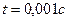 , выбрав в качестве материала медь.
, выбрав в качестве материала медь.
Для этого в командном окне надо выполнить следующую последовательность действий:
>>m='Cu';
>> v=mview(m)
v =
la=3.85;ce=0.465;ro=08.9;at=0.94;A=063.54;qpl=231.69;qis=5195.6;Tpl=1083;Tkp=2360;kev=6.0039e6;kdh=05;
>> eval(v)
В первой строке задаётся имя материала, во второй с помощью специальной программы mview, текст которой приведён в приложении, из массива mat извлекаются значения теплофизических констант вместе с зарезервированными именами и в символьном виде помещаются в переменную v. В третьей строке происходит выполнение всех операторов присваивания, помещённых в переменной v, и все переменные вместе со своими значениями попадают в рабочую область памяти. Система готова к расчёту температурных полей. Введём в командном окне значение энергии, на удачу, диапазон изменения расстояния до точки воздействия Rm, шаг по радиусу – shR, и создадим вектор значений радиуса R с учётом того, что поле имеет центральную симметрию.
>> E=0.01;
>> Rm=0.06;
>> shR=Rm/100;
>> R=[-Rm:shR:Rm];
Значение времени будем задавать в векторной переменной t , предполагая, что в дальнейшем значений моментов времени будет несколько, а для записи результата подготовим массив T:
>> i=1;t(i)=0.0001;
>> T=[];
Теперь проведём вычисления по формуле (1) этого раздела:
>> bt=(ce*ro)*(t(i)*4*pi*at)^1.5;
>> Tv=20+(2*E/(bt)).*exp(-(R.^2)./(t(i)*4*at));
Результаты счёта будем накапливать в массиве T в виде столбцов
>> T=[T;Tv];
Нарисуем график с координатной сеткой:
>> plot(R,T), grid on
Изложенную процедуру вычислений удобно оформить в виде подпрограмм. Подпрограмма для вычисления зависимости T от расстояния R:
function T=Tpmtit(E,R,t,m)
%zavisimoct T ot R pri vremenax t;
vp=mview(m); - извлечение вектора теплофизических параметров материала по заданному имени m.
eval(vp); - введение имён и значении параметров в рабочую область памяти.
bt=(ce*ro)*(t*4*pi*at)^1.5; - вычисление температуры.
T=20+(2*E/(bt))*exp(-(R.^2)./(t*4*at)); - вычисление температуры.
В подпрограмме набор значений R задаётся при вызове в виде вектора.
Эту подпрограмму можно включить в программу вычисления зависимостей T от R для набора моментов времени.
Исследуем зависимость распределения температуры в материале от времени при некотором фиксированном расстоянии 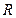 до точки воздействия МТИ.
до точки воздействия МТИ.
Поступим аналогично предыдущему:
>>m='Cu';
>> v=mview(m);
>> eval(v)
>> T=[];
>> T0=20;
>> E=0.1;
>>tk=0.0003;
>> sh=tk/200;
>> t=[sh:sh:tk];
Здесь tk – конечное значение интервала времени, выбрано на удачу, T0=20 – начальное значение температуры. Если интервал оказывается велик или мал, его можно подобрать опытным путём при счёте. Подготовка закончена. Теперь проведём вычисления по формуле (1) этого раздела:
>> R=0.01;
>> bt=(t*4*pi*at).^1.5;
>> rm=-(R.^2);
>> tm=1./(t*4*at);
>> bt=(t*4*pi*at).^1.5;
>> Tv=T0+(2*E./(ce*ro*bt)).*exp(tm.*rm);
>>Tv=Tv'
>> T=[T;Tv];
Изобразим график с координатной сеткой:
>> plot(t,T), grid on
Постройте графики для нескольких значений расстояния R в одном окне, накапливая значения температуры в массиве T.
Задача 1.Построить с помощью системы MatLab семейство графиков распределения температуры 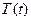 для фиксированного значения расстояния до центра источника
для фиксированного значения расстояния до центра источника 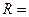 0.3см и различных материалов:
0.3см и различных материалов: 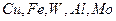 , сделать выводы.
, сделать выводы.
График 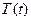 для вольфрама и меди показан на рис.1.
для вольфрама и меди показан на рис.1.
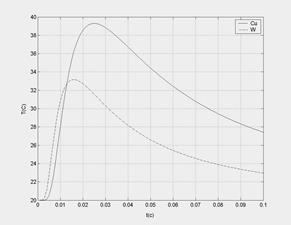
Рис. 1
Как видно из рассмотрения графиков, зависимости температуры от времени имеют максимум.
Выведем формулу зависимости расстояния 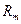 от времени
от времени 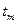 , за которое температура на этом расстоянии достигает максимального значения.
, за которое температура на этом расстоянии достигает максимального значения.
Решение: Найдём производную 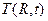 по времени и приравняем её к нулю:
по времени и приравняем её к нулю:
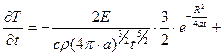
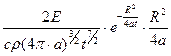 =0;
=0;
Сокращая, получим:
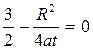 ;
;
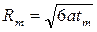 (3);
(3);
или: 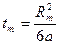 (4).
(4).
С помощью формул (3) и (4) можно определить масштабы времени и расстояния в приведённых вычислениях зависимостей температуры и оформить их в виде подпрограмм.
Подпрограмма №1 вычисления зависимости температуры от расстояния:
function [R,T]=Tpmr(E,t,m)
%zavisimoct T ot R pri vremenax t; Е - энергия импульса Дж, t –вектор времён, m – имя материала – формальные входные параметры. R,T – векторные выходные переменные, расстояние(см) и температура( 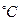 ) – соответственно.
) – соответственно.
vp=mview(m); - извлечение вектора теплофизических параметров материала о заданному имени m.
eval(vp); - введение имён и значении параметров в рабочую область памяти.
T=[]; - создание пустого массива результата.
n=length(t); - определение количества элементов в векторе времён.
tm=max(t); - нахождение максимального времени.
Rm=2*sqrt(6*at*tm); - определение максимального расстояния от точки воздействия: удвоенное значение по формуле (3).
shR=Rm/100; - шаг по R.
R=[-Rm:shR:Rm]; - вектор расстояний.
for i=1:n; - цикл по i, где i – номер значения времени в векторе t.
T=Tpmtit(E,R,t(i),m)
T=[T;Tv]; - накопление результата в массиве T.
end - конец цикла.
T=T'; - транспонирование Т для изображения результатов в одном окне.
Пример обращения к подпрограмме:
>> E=0.1;t=[0.0001:0.0001:0.0004];m='Cu';
>> [R,T]=Tpmt(E,t,m);
>> plot(R,T), grid on
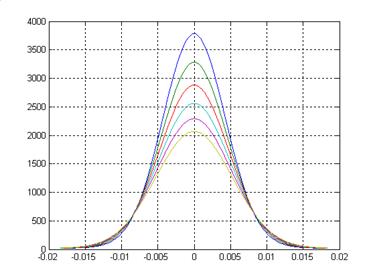
Рис.2
Результаты счёта приведены на рисунке 2.
Замечание: комментарии, набранные с наклоном в реальной программе должны отсутствовать.
Подпрограмма №2 вычисления зависимости температуры от времени:
function [t,T]=Tmpt (E,R,m)
%zavisimocti T ot t v tochkax R;
v=mview(m);
eval(v)
T=[];
n=length(R);
Rmax=max(R);
tk=3*(Rmax^2/(6*at));
sh=tk/200;
t=[sh:sh:tk];
T0=20;
for i=1:n;
bt=(t*4*pi*at).^1.5;
rm=-(R(i)^2) ./(t*4*at);
Tv=T0+(2*E./(ce*ro*bt)).*exp(rm);
end
T=[T;Tv];
T=T';
Приведённая программа отличается от предыдущей тем, что расчёт температуры ведётся в функции времени, а расстояние является параметром.
Пример обращения к подпрограмме:
>> E=0.01; R=[0.006:0.0004:0.0072];;m='Cu';
>> [t,T]=Tpmt(E,t,m);
>> plot(t,T), grid on
Результаты счёта приведены на рисунке 3.
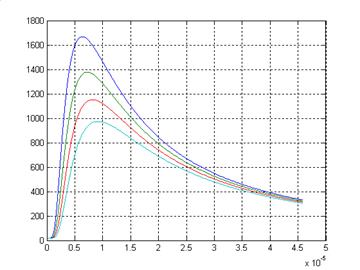
Рис. 3
Задача 2: Вывести формулу для определения значения максимальной температуры 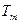 на расстоянии
на расстоянии 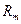 , достигаемой за время
, достигаемой за время 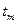 .
.
Решение: Подставим значения температуры и времени из формул (3) и(4) в формулу температурного поля (1) и проведём преобразования:
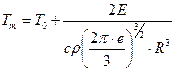 ;
; 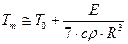 (5).
(5).
Задача 3: Вывести формулу для определения радиуса пятна нагрева 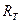 , внутри которого температура выше некоторой заданной величины
, внутри которого температура выше некоторой заданной величины 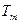 , определить объём материала
, определить объём материала 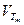 , находящегося внутри изотермической поверхности
, находящегося внутри изотермической поверхности 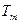 .
.
Решение: Разрешим формулу (5) относительно радиуса 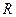 :
:
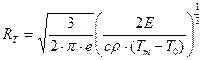 ;
; 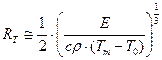 (6).
(6).
Объём 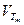 :
:
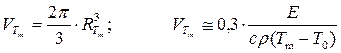 (7).
(7).
Если Tm=Tпл, то 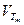 - это объём расплава -
- это объём расплава - 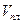 .
.
Температура внутри круга с радиусом 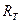 будет превосходить температуру
будет превосходить температуру 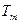 .
.
Эта оценка объёма расплава не учитывает теплоту необходимую для превращения металла из твёрдого состояния в жидкое - скрытую теплоту плавления. Для оценки этого влияния определим соотношение между скрытой теплотой плавления единицы объёма материала 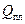 и количеством тепла необходимого для нагрева этого объёма до температуры плавления
и количеством тепла необходимого для нагрева этого объёма до температуры плавления 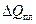 :
:
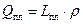 ;
; 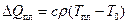 ;
; 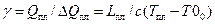 ;
;
где: 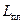 - скрытая теплота плавления
- скрытая теплота плавления 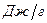 . Например для меди, соотношение
. Например для меди, соотношение 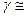 0,46, и, следовательно, объём расплава будет примерно в два раза меньше.
0,46, и, следовательно, объём расплава будет примерно в два раза меньше.
Задача 4. С помощью системы MATLAB вычислить значения объёмов расплава и значений 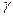 для различных материалов:
для различных материалов: 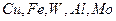 , при фиксированной энергии 0.01 Дж, результаты свести в таблицу, сделать выводы.
, при фиксированной энергии 0.01 Дж, результаты свести в таблицу, сделать выводы.
Определим, теплосодержание материла, находящегося внутри изотермической поверхности с радиусом 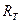 . Для этого определим среднее приращение температуры по формуле (4) предыдущего раздела, подставив в неё выражение для приращения температуры (1).
. Для этого определим среднее приращение температуры по формуле (4) предыдущего раздела, подставив в неё выражение для приращения температуры (1).
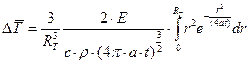 (8).
(8).
Вычислим интеграл в правой части выражения с помощью MATLAB. Обозначим выражение подынтегральной функции – y, а переменную интегрирования x и выполним следующую последовательность действий:
>> syms x a R t;- провозглашение символьных переменных интегрирования;
>> y=x^2*exp(-x^2/(4*a*t)); - задание подынтегральной функции;
>> int(y,0,R) – вычисление определённого интеграла от 0 до R.
После исполнения получим следующий результат:
-2*a*t*(R*exp(-1/4*R^2/a/t)*(1/a/t)^(1/2)-pi^(1/2)*erf(1/2*R*(1/a/t)^(1/2)))/(1/a/t)^(1/2).
Перепишем в обычном виде, вернёмся к первоначальным обозначениям и подставим значение интеграла в (8):
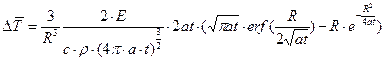 (9).
(9).
Если 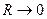 и
и 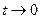 , то
, то 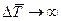 , если
, если 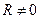 , а
, а 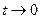 , то температура конечна, и зависит от радиуса, если при этом
, то температура конечна, и зависит от радиуса, если при этом 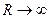 , то
, то 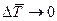 .
.
Задача 5: С помощью MATLAB построить зависимости среднего приращения температуры от времени для различных значений радиуса изотермической поверхности - R. Для различных материалов и различных значений энергии источника тепла. Оформить вычисления в виде подпрограммы.
Найдём среднее приращение температуры для объёма ограниченного изотермической поверхностью, соответствующей максимуму температуры 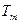 . Для этого сначала подставим в (9) значение времени
. Для этого сначала подставим в (9) значение времени 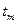 из (4):
из (4):
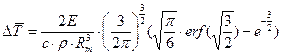 ; (10);
; (10);
а затем подставим значение радиуса 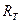 из (6) и, упростив выражение, получим среднее приращение температуры материала, находящегося внутри изотермической поверхности с температурой
из (6) и, упростив выражение, получим среднее приращение температуры материала, находящегося внутри изотермической поверхности с температурой 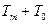 :
:
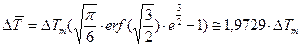 (11).
(11).
Таким образом, среднее приращение температуры внутри изотермической поверхности 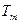 превосходит приращение температуры на самой поверхности.
превосходит приращение температуры на самой поверхности.
Определим долю энергии источника, содержащуюся в материале, находящемся внутри изотермической поверхности с температурой 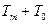 . Подставим в формулу (3) введения значение объёма из (6) и среднее значение температуры, получим:
. Подставим в формулу (3) введения значение объёма из (6) и среднее значение температуры, получим:
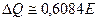 (12).
(12).
Задача 6:Вывести формулу зависимости радиуса изотермической поверхности 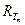 от времени.
от времени.
Решение: Из формулы температурного поля (1), выразим радиус, считая температуру заданной и равной 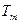 :
:
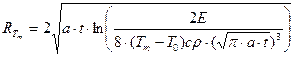 (7);
(7);
Задача 7: С помощью системы MATLAB построить зависимости 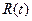 по формуле (7) для меди, при энергии импульса 100Дж, для температур плавления и кипения. Оформить вычисления в виде подпрограммы. При составлении подпрограммы необходимо выбрать диапазон изменения времени, при этом следует учесть, что подкоренное выражение должно быть не отрицательным. Следовательно, выражение под логарифмом должно быть больше или равно единицы. Таким образом, верхнее граничное значение времени может быть определено с помощью неравенства:
по формуле (7) для меди, при энергии импульса 100Дж, для температур плавления и кипения. Оформить вычисления в виде подпрограммы. При составлении подпрограммы необходимо выбрать диапазон изменения времени, при этом следует учесть, что подкоренное выражение должно быть не отрицательным. Следовательно, выражение под логарифмом должно быть больше или равно единицы. Таким образом, верхнее граничное значение времени может быть определено с помощью неравенства:
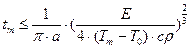
Графики приведены на рисунке 4. Прокомментируйте их.
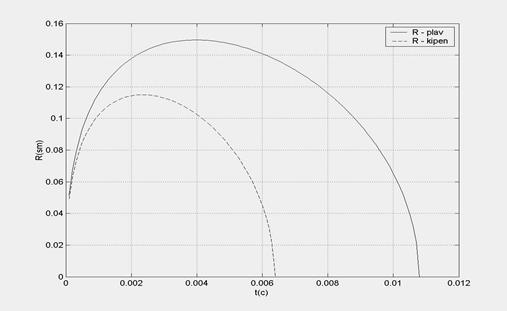
Рис. 4
Мгновенный точечный источник теплоты может быть использован для нахождения температурных полей остросфокусированных источников, время действия которых, много меньше времени достижения температурным фронтом границ обрабатываемой детали.
