Общая схема исследования функций и построения графиков

Алгоритм исследования функции у = f (х):

1. Найти область определения функцииD (y).

2. Найти (если это можно) точки пересечения графика с осями координат (при x = 0 и при y = 0).

3. Исследовать на четность и нечетность функции(y (‒x) = y (x) ‒четность; y(‒x) = ‒y (x) ‒нечетность).

4. Найти асимптоты графика функции.

5. Найти интервалы монотонности функции.

6. Найти экстремумы функции.

7. Найти интервалы выпуклости (вогнутости) и точки перегиба графика функции.

8. На основании проведенных исследований построить график функции.

Пример.Исследовать функцию и построить ее график.

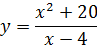
1) D (y) =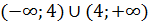

x = 4 ‒ точка разрыва.

2) При x = 0,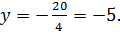

(0; ‒ 5) ‒ точка пересечения с oy.

При y = 0,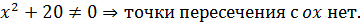

3) y(‒ x)= 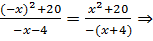функция общего вида (ни четная, ни нечетная).

4) Исследуем на асимптоты.

а) вертикальные

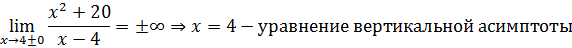
б) горизонтальные

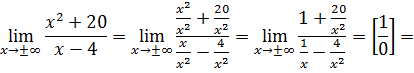
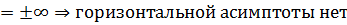
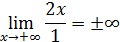
в) найдем наклонные асимптоты 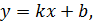где

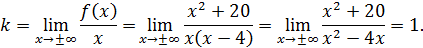
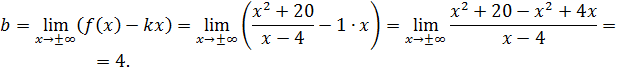
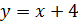‒ уравнение наклонной асимптоты

5) В данном уравнении не требуется найти интервалы монотонности функции.

6)

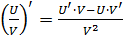
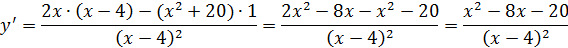
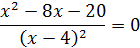
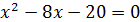
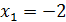
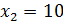
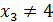
Эти критические точки разбивают всю область определения функции на интервале (˗∞; ˗2), (˗2; 4), (4; 10)и (10; +∞). Полученные результаты удобно представить в виде следующей таблицы:

x	(˗∞; ˗2)	˗2	(˗2; 4)		(4; 10)		(10; +∞)
	+		˗		˗		+
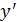y		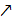max		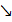нет экстр.		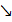min

Из таблицы видно, что точках = ‒2‒точка максимума, в точкех = 4‒нет экстремума, х = 10 ‒точка минимума.

Подставим значение (‒ 3) в уравнение:

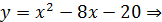9 + 24 ‒ 20 > 0

0 ‒ 20 < 0

25 ‒ 40 ‒ 20 < 0

121 ‒ 88 ‒ 20 > 0

Максимум этой функции равен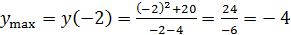

(‒ 2; ‒ 4) ‒ экстремум максимальный.

Минимум этой функции равен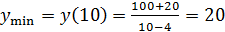

(10; 20) ‒ экстремум минимальный.

7) исследуем на выпуклость и точку перегиба графика функции

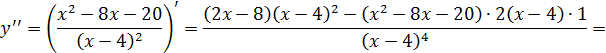
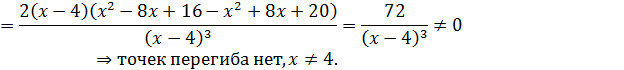
8)

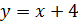
x
y

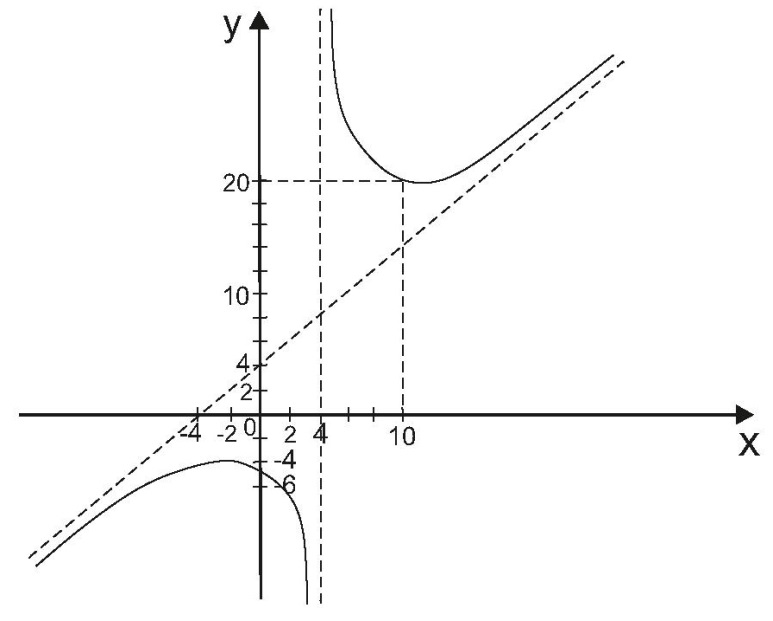
ПЕРВООБРАЗНАЯ ФУНКЦИЯ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА.

Функцию, восстанавливаемую по ее производной или дифференциалу, называют первообразной.

Определение.Функция F(x) называется первообразной для функции

f(x) на некотором промежутке, если в каждой точке этого промежутка

F'(x) = f(x)

или, что тоже,

dF(x) = f(x)dx

Например, F(x) = sin x является первообразной для f(x) = cos x на всей числовой оси OХ, так как

(sin x)' = cos x

Если функция F(x) есть первообразная для функции f(x) на [a;b], то функцияF(x) + С, где Cлюбое действительное число, также является первообразной для f(x)при любом значении C. Действительно (F(x) + C)' = F'(x) + C' = f(x).

Пример.

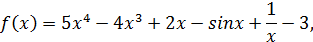
тогда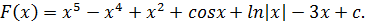

Определение.Если F(x) одна из первообразных для функции f(x) на [a;b], то выражение F(x) + С, где C произвольная постоянная, называется неопределенным интегралом от функции f (x) и обозначается символом ʃ f (x) dx (читается: неопределенный интеграл от f(x) на dx). Итак,

ʃf(x)dx = F(x) + C ,

где f(x) называется подынтегральной функцией, f(x)dx‒ подынтегральным выражением, x ‒ переменной интегрирования, а символ ʃ‒ знаком неопределенного интеграла.