Таблицы продолжительности жизни

Статистические данные о продолжительности жизни суммируются в таблицах продолжительности жизни, иногда их называют таблицами смертности. Простейшим видом таблиц являются таблицы, содержащие информацию о статистических свойствах времени жизни случайно выбранного человека, относительно которого известен только его возраст. Такие таблицы называют общими или упрощенными. Они позволяют получить общую приближенную картину смертности. Примером таких таблиц могут служить популяционные таблицы, содержащие данные о смертности населения. В принципе для решения любой задачи достаточно знания функции выживания 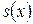, однако для наглядности в таблицы обычно включают введенные ранее величины:

1) 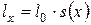– среднее число живых представителей некоторой группы из 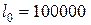новорожденных к возрасту лет.

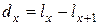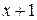2) – число представителей группы, умерших в возрасте от до лет.

3) 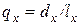– вероятность смерти в течение года для человека в возрасте лет.

4) 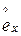– среднее остаточное время жизни.

В качестве шага таблицы обычно рассматривают один год.

Таблицы отбора риска

Очевидно, что статистические свойства продолжительности жизни различны у жителя высокоразвитой страны Запада и жителя бедного африканского государства, поэтому абсолютно общая таблица не представляет реального интереса.

Однако и среди жителей одной страны существуют различные группы людей с разными характеристиками продолжительности жизни. Прежде всего, важно отметить, что смертность среди мужчин в несколько раз выше смертности среди женщин. Вероятно, смертность среди домохозяек меньше, чем среди шахтеров; смертность среди людей, прошедших медкомиссию перед заключением договора страхования, меньше, чем в среднем по стране; смертность среди людей, вышедших на пенсию по болезни, наоборот, выше (конечно, во всех случаях мы должны сравнивать людей в одном возрасте ). Но страховая компания имеет дело не с абстрактными людьми, а с вполне конкретными, относительно которых доступна определенная информация (пол, профессия, перенесенные болезни и т.д.). Поэтому ясно, что компания должна иметь целый спектр таблиц продолжительности жизни для различных групп населения. Такие таблицы называются таблицами отбора риска. Обычно создается несколько базовых таблиц, а многочисленные дополнительные риски учитываются с помощью руководств по андеррайтингу, которые дают соответствующие коэффициенты (или аддитивные надбавки) к базовым тарифам.

Термин «отбор» связан с тем, что люди попадают в группу, для которой составляется таблица, после некоторого отбора. Иногда этот отбор кем-то специально проводится (например, медицинской комиссией перед заключением договора страхования), иногда человек сам отбирает себя (например, при оформлении пожизненной ренты), иногда это происходит по причине внешних обстоятельств (например, при оформлении пенсии по болезни). Смертность среди людей, включенных в такую группу, зависит не только от возраста 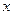, но и от того, когда произошел отбор. Рассмотрим, например, людей, успешно прошедших медицинский андеррайтинг и заключивших договоры страхования. Ясно, что вероятность смерти в течение ближайшего года человека из этой группы существенно меньше, чем вероятность смерти в течение ближайшего года случайно выбранного человека в том же возрасте. Более интересно то, что вероятность смерти в течение ближайшего года человека, только что прошедшего отбор, меньше, чем вероятность смерти в течение года человека в том же возрасте, но прошедшего отбор несколько лет тому назад. Например, вероятность смерти мужчины в возрасте 52 года по данным страховой статистики Великобритании 1970–1972 гг. составляет 0,344% для первого года договора, 0,429 – если с момента заключения договора прошел уже год и 0,603%, если договор был заключен 2 или больше лет тому назад.

В связи с этим величины, включенные в таблицы с отбором, имеют два аргумента: один показывает момент отбора , а второй – время , прошедшее с момента отбора. В актуарной математике эту зависимость обозначают 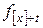. При фиксированном возрасте 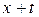и моменте отбора 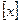величина 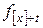ничем принципиально не отличается от величины 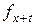. Поэтому для характеристик продолжительности жизни «отобранных» людей справедливы все приведенные выше результаты, а именно:

1) 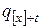обозначает условную вероятность смерти в течение года человека в возрасте 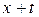лет, который лет назад (т.е. в возрасте лет) был отобран в группу;

2) 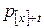– вероятность того, что человек в возрасте 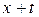лет, который лет назад (т.е. в возрасте лет) был отобран в группу, проживет еще по меньшей мере год;

3) 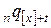– вероятность того, что человек в возрасте 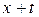лет, который лет назад (т.е. в возрасте лет) был отобран в группу, умрет на протяжении ближайших лет;

4) 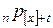– вероятность того, что человек в возрасте 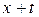лет, который лет назад (т.е. в возрасте 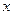лет) был отобран в группу, проживет еще по меньшей мере лет;

5) 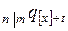– вероятность того, что человек в возрасте 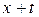лет, который отобран лет назад, проживет лет, но умрет на протяжении 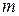последующих лет;

6) 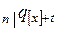– вероятность того, что человек в возрасте 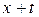лет, который отобран лет назад, проживет лет, но умрет на протяжении следующего года.

Все эти вероятности могут быть выражены через вероятности 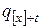, например,

, .

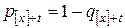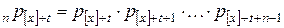Таблицы с отбором ограниченного действия

Статистический анализ показывает, что обычно влияние отбора продолжается неограниченно долго. Однако, как правило, зависимость характеристик смертности от времени, прошедшего с момента отбора, быстро уменьшается и через некоторое время эти характеристики зависят только от достигнутого возраста. Влияние отбора сохраняется в том смысле, что эти характеристики отличаются от популяционных.

Промежуток времени 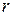, после которого зависимостью от момента отбора можно пренебречь и рассматривать все характеристики продолжительности жизни только как функции достигнутого возраста, называется периодом действия отбора.

Соответствующая таблица называется таблицей с отбором ограниченного действия. Предельные значения 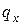(которые заменяют 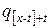при 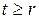) образуют так называемую предельную таблицу. По своей структуре она является таблицей простейшего типа.

Расчет характеристик смертности среди представителей выделенной группы может быть значительно упрощен, если вместо вероятностей 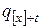ввести в рассмотрение специальные величины 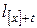, которые аналогичны величинам 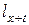из общих таблиц смертности.

Рассмотрим некоторую таблицу с отбором, действующим 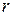лет, и определим величины 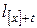с помощью следующей формулы:

.

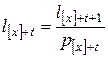Поскольку период действия отбора равен 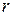, полагаем 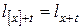, если 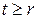. Тогда

, ,

, .

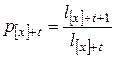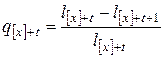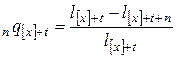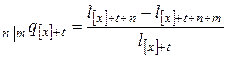Поэтому часто в таблицы с отбором ограниченного действия включаются только величины 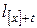.