Тема «Функции действительного переменного»
Вариант 1
1. Решить уравнение 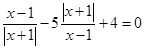
2. Найти область определения функции 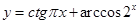
3. Построить график: 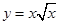
4. Является ли множество чисел 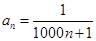 для
для 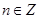 ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
5. Тождественны ли функции: 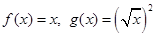 .
.
6. Выразить зависимость длины одного катета прямоугольного треугольника от длины другого катета, если гипотенуза постоянная величина равная 5.
7. Построить сечение множества действительных чисел, определяющих число 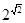 . Доказать, что в одном классе нет наибольшего числа, а в другом классе нет наименьшего числа.
. Доказать, что в одном классе нет наибольшего числа, а в другом классе нет наименьшего числа.
Вариант 2
1. Решить уравнение 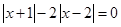
2. Найти область определения функции 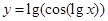
3. Построить график: 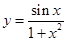
4. Является ли множество чисел 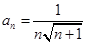 для
для 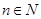 ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
5. В сосуд налита вода. На глубине 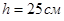 давление этой жидкости
давление этой жидкости 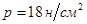 . Составить функцию, выражающую зависимость давления от глубины.
. Составить функцию, выражающую зависимость давления от глубины.
6. Даны функции: 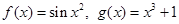 , найти вид следующих функций:
, найти вид следующих функций: 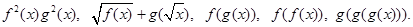
7. Сечение множества действительных чисел, определяющее число 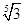 , строится так: один класс содержит все рациональные числа а такие, что
, строится так: один класс содержит все рациональные числа а такие, что 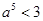 , другой класс другой класс содержит все остальные рациональные числа.. Доказать, что в одном классе нет наибольшего числа, а в другом классе нет наименьшего числа.
, другой класс другой класс содержит все остальные рациональные числа.. Доказать, что в одном классе нет наибольшего числа, а в другом классе нет наименьшего числа.
Вариант 3
1. Решить уравнение 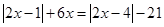
2. Найти область определения функции 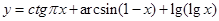
3. Построить график: 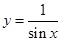
4. Является ли множество чисел 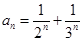 для
для 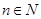 ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
5. Доказать, что сумма двух четных функций есть четная функция; сумма двух нечетных функций есть нечетная функция;
6. Тождественны ли функции: 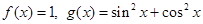 .
.
7. Сечение множества действительных чисел, определяющее число 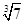 , строится так: один класс содержит все рациональные числа а такие, что
, строится так: один класс содержит все рациональные числа а такие, что 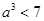 , другой класс другой класс содержит все остальные рациональные числа.. Доказать, что в одном классе нет наибольшего числа, а в другом классе нет наименьшего числа.
, другой класс другой класс содержит все остальные рациональные числа.. Доказать, что в одном классе нет наибольшего числа, а в другом классе нет наименьшего числа.
Вариант 4
1. Решить уравнение 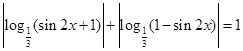
2. Найти область определения функции 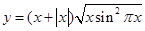
3. Построить график: 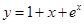
4. Является ли множество чисел 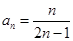 для
для 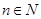 ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
5. Выразить площадь равнобедренной трапеции с основаниями 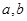 , как функцию угла
, как функцию угла 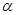 при основании
при основании 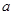 .
.
6. Функция 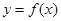 определена на отрезке
определена на отрезке 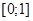 . Каковы области определения функций:
. Каковы области определения функций: 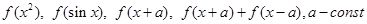
7. Сечение множества действительных чисел, определяющее число 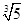 , строится так: один класс содержит все рациональные числа а такие, что
, строится так: один класс содержит все рациональные числа а такие, что 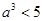 , другой класс другой класс содержит все остальные рациональные числа. Доказать, что в одном классе нет наибольшего числа, а в другом классе нет наименьшего числа.
, другой класс другой класс содержит все остальные рациональные числа. Доказать, что в одном классе нет наибольшего числа, а в другом классе нет наименьшего числа.
Вариант 5
1. Решить неравенство 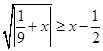
2. Найти область определения функции 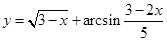
3. Построить график: 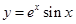
4. Является ли множество чисел 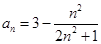 для
для 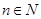 ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
5. Доказать, что множества 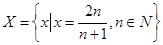 и
и 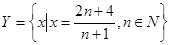 разделяются только одним числом 2.
разделяются только одним числом 2.
6. Придумать пример аналитической функции определенной только для 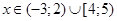
7.Выразить диаметр окружности, описанной около треугольника, как функцию угла 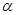 , лежащего против заданной стороны треугольника а.
, лежащего против заданной стороны треугольника а.
Вариант 6
1. Решить систему уравнений 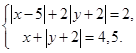
2. Найти область определения функции 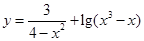
3. Построить график: 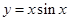
4. Является ли множество чисел 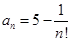 для
для 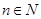 ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
5. Прямоугольный треугольник, сторона которого равна 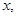 вписан в окружность радиуса
вписан в окружность радиуса 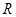 . Найти периметр
. Найти периметр 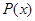 этого треугольника.
этого треугольника.
6. Пусть 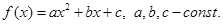 Показать, что
Показать, что 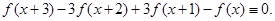
7.Сечение множества действительных чисел, определяющее число 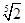 , строится так: один класс содержит все рациональные числа а такие, что
, строится так: один класс содержит все рациональные числа а такие, что 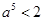 , другой класс другой класс содержит все остальные рациональные числа. Доказать, что в одном классе нет наибольшего числа, а в другом классе нет наименьшего числа.
, другой класс другой класс содержит все остальные рациональные числа. Доказать, что в одном классе нет наибольшего числа, а в другом классе нет наименьшего числа.
Вариант 7
1. Решить неравенство 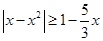
2. Найти область определения функции 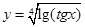
3. Построить график: 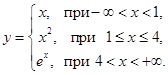
4. Является ли множество чисел 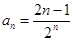 для
для 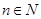 ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
5. В шар радиуса 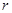 вписан цилиндр. Выразить объем этого цилиндра, как функцию его высоты. Найти область определения этой функции, найти множество значений полученной функции.
вписан цилиндр. Выразить объем этого цилиндра, как функцию его высоты. Найти область определения этой функции, найти множество значений полученной функции.
6. Доказать, что множества 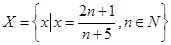 и
и 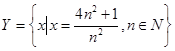 разделяются любым числом отрезка [2;4].
разделяются любым числом отрезка [2;4].
7.Сечение множества действительных чисел, определяющее число 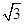 , строится так: один класс содержит все рациональные числа а такие, что
, строится так: один класс содержит все рациональные числа а такие, что 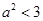 , другой класс другой класс содержит все остальные рациональные числа. Доказать, что в одном классе нет наибольшего числа, а в другом классе нет наименьшего числа.
, другой класс другой класс содержит все остальные рациональные числа. Доказать, что в одном классе нет наибольшего числа, а в другом классе нет наименьшего числа.
Вариант 8
1. Решить систему уравнений 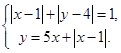
2. Найти область определения функции 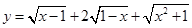
3. Построить график: 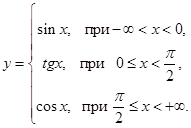
4. Является ли множество чисел 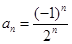 для
для 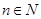 ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
5. В треугольнике АВС сторона АВ=6 см, сторона АС=8 см и угол ВАС равен х. Выразить сторону ВС=а и площадь треугольника, как функции угла х, построить их графики.
6. Дана функция 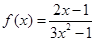 . Найти:
. Найти: 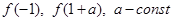 . Существует ли
. Существует ли 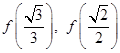
7. Выразить радиус основания конуса как функцию его высоты при заданном объеме 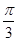 .
.
Вариант 9
1. Решить уравнение 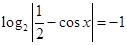
2. Найти область определения функции 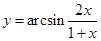
3. Построить график: 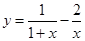
4. Является ли множество чисел 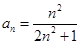 для
для 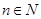 ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
5. Газ при давлении р=1атм занимает объем 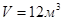 . Выразить изменение объема газа в зависимости от давления р, если температура газа остается постоянной.
. Выразить изменение объема газа в зависимости от давления р, если температура газа остается постоянной.
6. Переменная х пробегает интервал 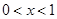 , какое множество пробегает переменная у, если
, какое множество пробегает переменная у, если 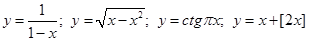
7. Выразить площадь прямоугольного треугольника, как функцию его катета при условии, что периметр этого треугольника равен 2р.
Вариант 10
1. Решить уравнение 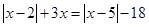 .
.
2. Найти область определения функции 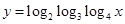
3. Построить график: 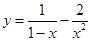
4. Является ли множество чисел 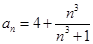 для
для 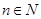 ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
ограниченным сверху, снизу. Найти точную нижнюю и точную верхнюю грани.
5. В равносторонний треугольник, сторона которого равна 6 см, вписан прямоугольник высотой х. Выразить площадь этого прямоугольника, как функцию от х.
6. Составить композицию функций 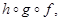 если
если 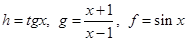
7. Выразить радиус шара, как функцию его объема.
