Применение нейронных технологий в системах связи

Эволюция сетей связи с подвижными объектами осуществляется в на­правлении обеспечения интегральных услуг предоставляемых пользова­телям.

Предоставление интегральных услуг для любых пользователей тесно связано с использованием цифровых методов передачи всех видов ин­формации, представленной в едином пакетном виде и использовании ме­тодов множественного доступа (МД). К таким методам можно отнести семейство гибридных методов, основанных на временном, кодовом и частотном разделении каналов. Гибридные методы доступа по­зволяют найти компромисс между обеспечиваемым гарантированным временем доставки сообщений при использовании детерминированных методов доступа и высокой степенью использования пропускной способ­ности канала, присущей большинству случайных методов МД. Однако высокая степень использования пропускной способности канала при слу­чайном МД достигается при определенной (оптимальной) входной на­грузке. При увеличении поступающей нагрузки сверх допустимого поро­гового значения коэффициент использования пропускной способности канала снижается. Эффективность использования ресурсов пропускной способности канала и в гибридных, и в случайных методах МД может быть существенно повышена при управлении потоком пакетов посту­пающих в радиоканал. В качестве управляемого параметра может исполь­зоваться вероятность первичной и повторной передачи пакетов в радиока­нал. Влияние выбора вероятности передачи на поддержание коэффициен­та использования пропускной способности канала МД можно пояснить следующим образом. Для подсистемы радиодоступа при малом значении вероятности повторной передачи у абонентов, в канале МД имеется большое количество свободных временных окон. При значительном уве­личении вероятности повторной передачи возрастает число конфликтных ситуаций. И в первом и во втором случае пропускная способность капала используется не полностью. Управление вероятностью передачи и выбор ее оптимального значения позволяет поддерживать коэффициент исполь­зования пропускной способности канала МД на почти постоянном, близ­ком к максимально возможному, уровне. В ряде работ доказана теорема о существовании такой вероятности повторной передачи 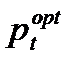и ее влиянии на эффективность функционирования сети в целом. Управление значением 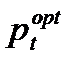осуществляется на основе анализа пространства состоя­ний радиоканала. Для оценки пространства состояний складывающегося в канале множественного доступа и нахождения требуемого значения управляемого параметра предлагается использовать нейросетевые модели.

В общем виде модель управления p-настойчивым множественным дос­тупом может быть представлена в виде:

x(k+1) = f(x(k), u(k)) (2)

где u(k) - вектор входных сигналов, x(k+1) - вектор выходных сигналов, k=0,1, ... - дискретное время.

Частными случаями представления вида (2) являются четыре модели идентификации объектов управления (объект управления имеет один вход и один выход). Эти модели могут быть описаны следующими нели­нейными разностными уравнениями:

Модель 1. 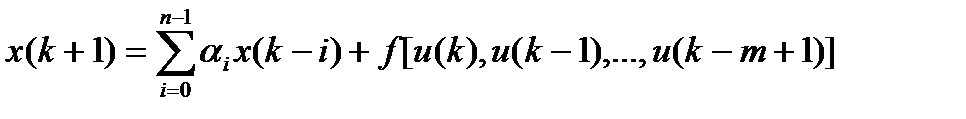(3)

Модель 2. x(k+l) = f[x(k), x(k-l), ... , x(k-n+l)]+ 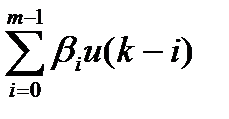(4)

Модель 3. x(k+l) = f[x(k), x(k-l) ,…, (k-n+l)] +g[u(k), u(k-l) , … , u(k-m+l)]. (5)

Модель 4. x(k+1) = f[x(k), x(k-1), ... , x(k-n+l); u(k), u(k-l), ... , u(k-m+1)]. (6)

где [u(k), x(k)] ­­­– пара значений входа-выхода в момент k.

Функции f и g являются дифференцируемыми по всем параметрам.

Модель 1: выход неизвестного нелинейного объекта управления зави­сит линейно от его предыдущих значений и нелинейно от предыдущих значений входа. Модель 1 показана на рис. 6 и состоит из секциониро­ванных линий задержки на входе и в цепи обратной связи.

Модель 2: может быть реализована как показано в рис. 7. В этом слу­чае выход зависит линейно от входа u(k) и его предыдущих значений и нелинейно от собственных предыдущих значений.

Модель 3: из нелинейного разностного уравнения (5) видно, что вы­ход нелинейного объекта управления зависит нелинейно как от предыду­щих значений входа, так и от предыдущих значений выхода. Схематичное представление нелинейного разностного уравнения для модели 3 приве­дено на рис. 8.

Модель 4: эта наиболее общая из всех моделей, представленных ранее. Выход в любой момент времени является нелинейной функцией преды­дущих значений и входа и выхода. Она изображена на рис. 9.

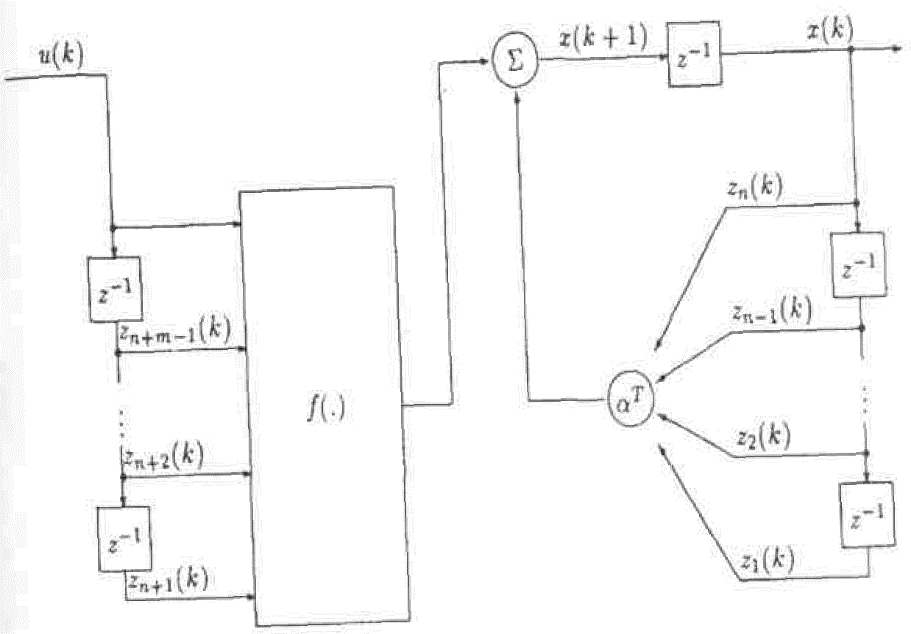
Рис. 6. Модель 1

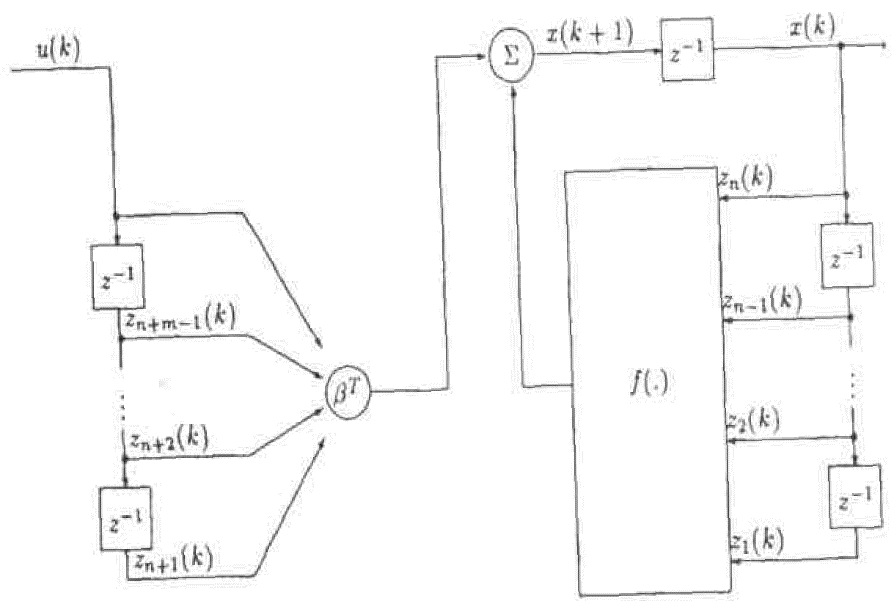
Рис. 7. Модель 2

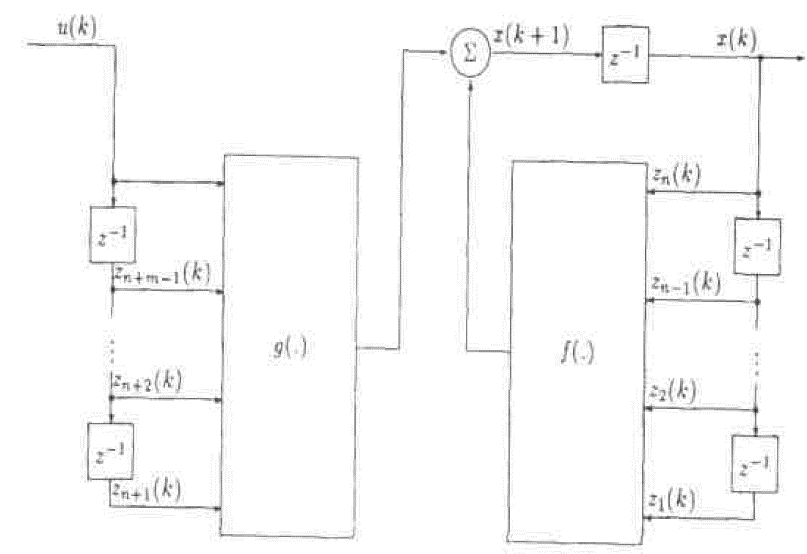
Рис. 8. Модель 3

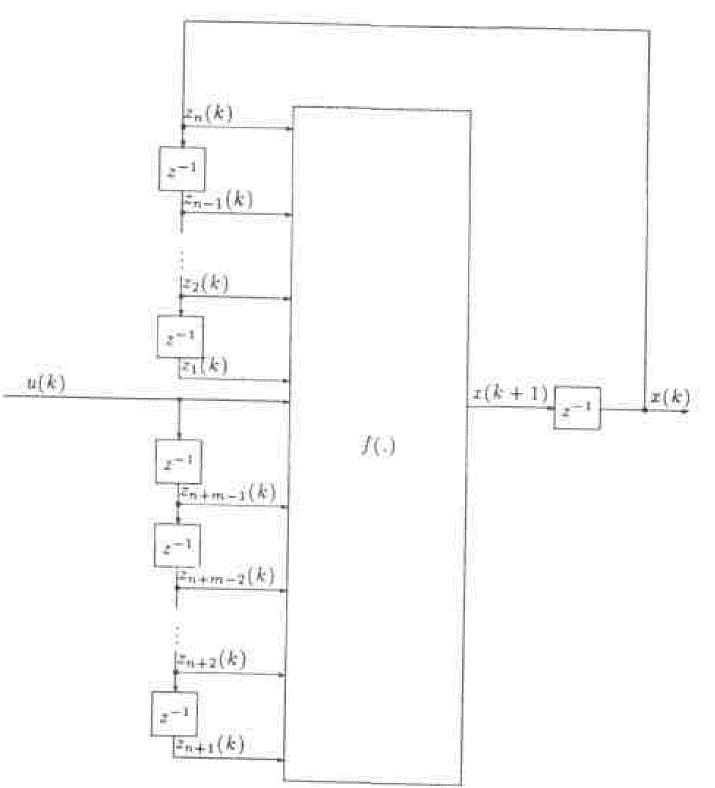
Рис. 9. Модель 4

Из (3)-(6) и рис. 6-9 следует, что модели идентификации объ­ектов управления в общем случае должны состоять из нейросетевых мо­делей и секционированных линий задержки. При этом используемая НС должна содержать достаточное для соответствующего нелинейного ото­бражения состояния объекта управления число слоев и узлов в каждом слое. С точки зрения математики это подразумевает, что нелинейные функции в разностных уравнениях, описывающих состояние объекта управления могут быть заменены нейросетевыми моделями с фиксиро­ванными матрицами весовых коэффициентов W. Чтобы правильно иден­тифицировать состояние объекта управления и на основе этого формиро­вать соответствующее управляющее воздействие модель идентификации должна выбираться на основе имеющейся информации относительно класса, которому принадлежит рассматриваемый объект.

При построении контроллера для управления р-настойчивым множе­ственным доступом могут использоваться типовые варианты реализации управляющих контроллеров, содержащих нейросетевые модели. Нейронная сеть будет являться одной из основных компонент системы управления. При этом НС используется в виде либо параллель­ной, либо последовательно-параллельной (рис. 10) модели. Настройка весов НС (обучение НС), может рассматриваться как процесс ее адапта­ции к выбранной системе управления.

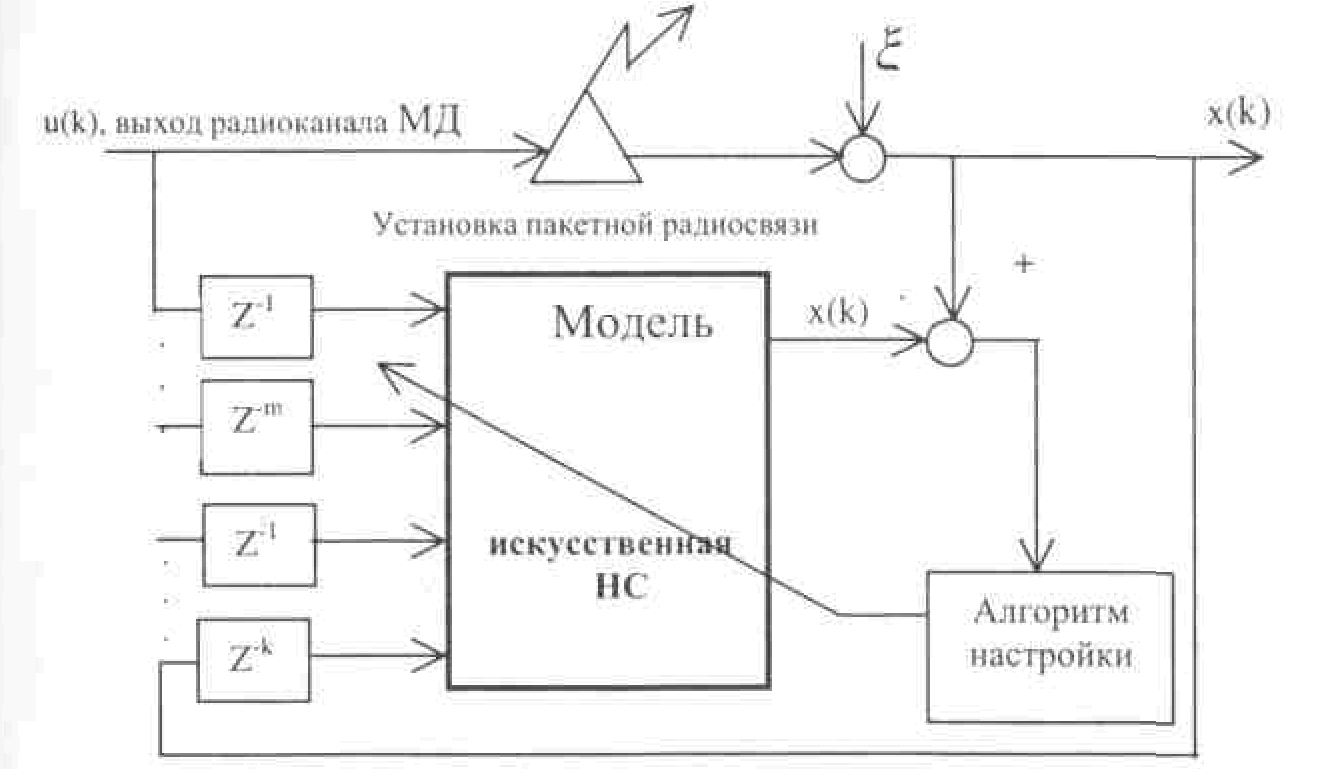
Рис. 10. Обобщенная модель управления р-настойчивым множественным доступом

Вариант использования многослойной НС для решения задачи децен­трализованного управления р-настойчивым МД представлен на рис. 11.

Слева схематично изображен частотно-временной план тактированно­го радиоканала случайного МД. Предполагается, что возможно наличие трех событий: "Конфликт", "Успех", "Свободно" (пустое временное окно). Справа схематично изображена q-слойная НС с H_i, нейронами в i-м слое.

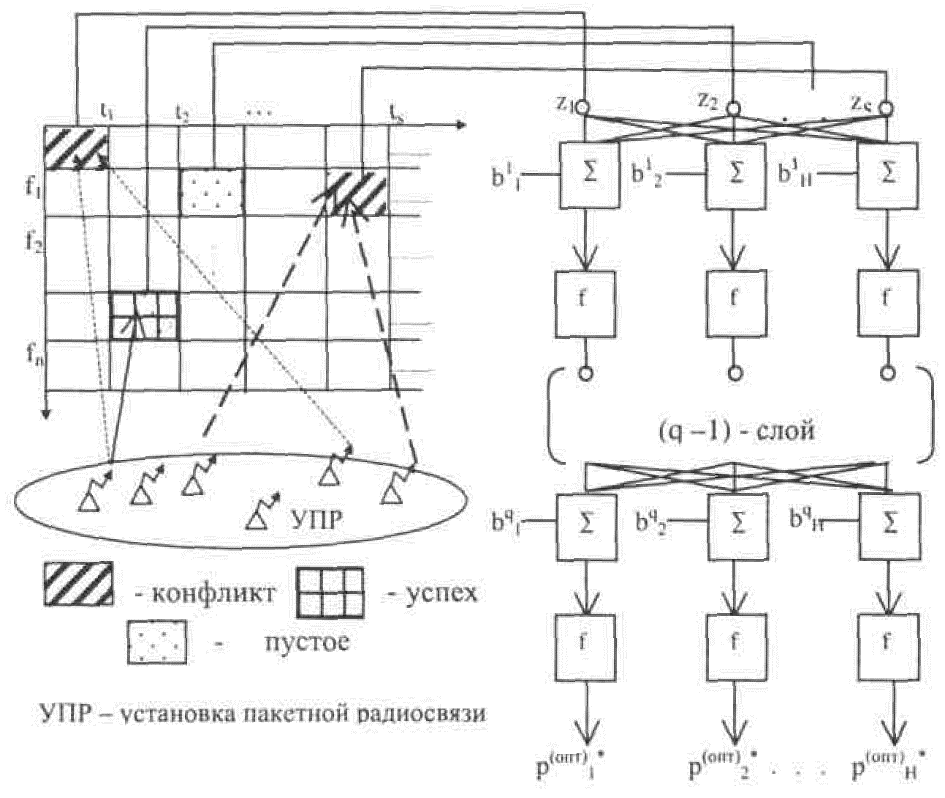
Рис. 11. Вариант использования НС для решении задачи управления МД

Математическая модель такой сети имеет вид:

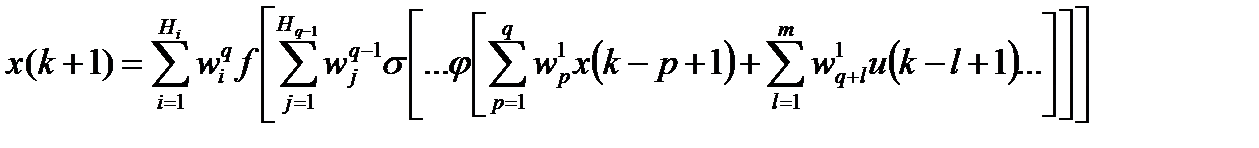(7)

или в векторно-матричной форме

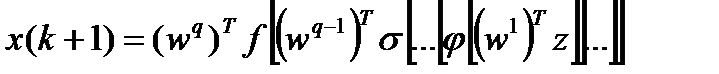(8)

Здесь х(·), u(·) – соответственно выходной и входной сигналы,

z = [у(·), u(·)]^T ; w^q – весовой коэффициент i-го нейрона в q-ом слое;

f(·),σ(·),φ(·) – функции активации.

Наиболее часто используется модель искусственной НС, содержащая помимо входного и выходного слоев, один скрытый слой. Кроме того, для простоты принимается, что все функции активации имеют одинаковый вид Для того случая уравнение (7) принимает вид

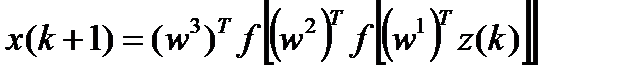(9)

где z(k) = [x(k), x(k-m+1); u(k), ... , u(k-m+1)]^Т.

Такая нейросетевая модель и была использована при компьютерном моделировании.

Для обучения многослойных НС может быть использовано несколько процедур, оптимизирующих некоторую функцию критерия с помощью градиентных методов первого и второго порядков, а также с помощью методов линеаризации. Обучающее множество должно быть представительным, что гарантирует правильную работу системы иденти­фикации даже в случае поступления на ее вход набора, не включенного в обучающее множество.

При моделировании среднеквадратическая шибка 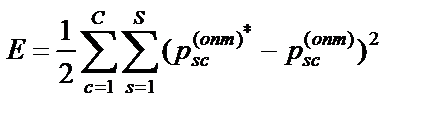рассчитывалась при использовании про­цедуры обратного распространения. Здесь через С обозначается число выборок образов в обучающем множестве, а через 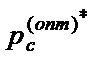={ 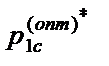, , 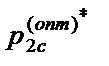… , 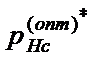}^E и 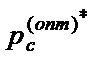={ 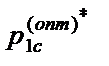, , 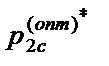… , 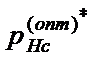}^T – получаемый и желаемый выходные векторы сети.

Использование НС для управления р-множественным доступом позволяет получать оптимальные значения вероятности повторной передачи в соответствии с выбранной стратегией при неизвестных ранее входных данных. Причем после завер­шения процесса обучения не требуется производить дополнительных вы­числений, и процесс принятия решения ускоряется.