Количественная оценка степени идентичности модели и исследуемого объекта
Известно, что при моделировании вероятных моделей заведомо не известная ни степень, ни форма зависимости между отдельными входными переменными, а также между входными и выходными переменными. Конечно, что мы хотим построить модель с учетом не всех переменных, а с учетом по возможности меньшей их количества.
Однако, это количество входных переменных должна определять исходную переменную с точностью не больше допустимой погрешности.
После выбора определенного числа входных переменных и построения по ним модели возникают задачи определения степени соответствия модели к реально исследуемого объекту. Решение такой задачи имеет большое практическое значение, так как разрешает определить правильность выбора тех или других переменных.
Пусть вектор входных переменных имеет вид:
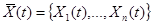 ,
,
а вектор выходных переменных:
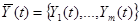 , где m ≤ n. Тогда можно последовательно определить значения оператора связи ai,j j - й выходной переменной от влияния i-й входной переменной.
, где m ≤ n. Тогда можно последовательно определить значения оператора связи ai,j j - й выходной переменной от влияния i-й входной переменной.
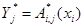 , если данное распределение системы двух случайных величин X1 на X2 то регрессией X1 на X2 называется произвольная функция g2(x1) приближенно представляющая статистическую зависимость вида:
, если данное распределение системы двух случайных величин X1 на X2 то регрессией X1 на X2 называется произвольная функция g2(x1) приближенно представляющая статистическую зависимость вида:
(1) 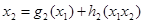 , где
, где 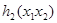 есть поправочными слагаемыми. В вообще среднеквадратичная регрессия x2 на x1 минимизирует квадрат отклонения вида
есть поправочными слагаемыми. В вообще среднеквадратичная регрессия x2 на x1 минимизирует квадрат отклонения вида
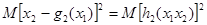
и кривая от Х2 носит название среднеквадратичной регрессии. Базируясь на парных результатах
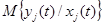 может быть построенная множественная регрессия
может быть построенная множественная регрессия 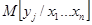 , которая, как правило, заменяется упрощенной
, которая, как правило, заменяется упрощенной 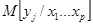 p<<n .Тогда оператор связи может быть оптимальной в понятии минимального среднего квадрата ошибки.
p<<n .Тогда оператор связи может быть оптимальной в понятии минимального среднего квадрата ошибки.
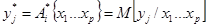 (2)
(2)
В этом выражении учитывается общее влияние на выходную переменную Yj всех учтенных P входных переменных.
Для того чтобы задача установления числа переменных P в выражении (2) стала определенной, необходимо задать некоторые требования к выходных переменных Yj. Обычно в качестве такого указателя рядом с мат. ожиданием используется дисперсия или корреляционная функция, которая заданная раньше. Дисперсия выходной переменной характеризуют точность, а корреляционная функция - те связи, которые присущи выходным переменным.
Общая дисперсия выходных переменных состоит из двух слагаемых:
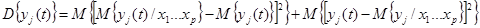 (3)
(3)
Первое слагаемое вызван влиянием P переменных, второй - учитывается влияние на формирование выходной переменной (n-p) переменных которые осталось.
Выходная переменная из выражения (3) должна удовлетворять соотношение
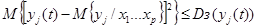 (4)
(4)
где Dз – заданная дисперсия
Очевидно, что если условие (4) выполняется при P=1, то достаточно модели, построенной с учетом одной переменного. Практически может быть такой случай, если введение новой переменной не приводит к достижению заданной цели. В таком случае необходимо изменить требования к представлению исходных переменных. Постановка задачи здесь должна быть связана с поиском оптимизации, то есть использование такого критерия, который обеспечит необходимые представления.
В конечном случае роль пойдет о количественной оценке идентичности модели и объекта. Таких критериев можно подобрать немало, мы же используем дисперсионную меру:
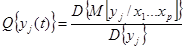
если P=n, то Q=1
P≠n, nj 0<Q<1
Объекты, для которых Q=1 называются регулярными или детерминированными (полностью определенными)
Q=0 - нерегулярные, стахостическими, случайные.
Оценка адекватности модели может быть:
1) Оценка адекватности концептуальной модели
2) Оценка достоверности ее реализации.
